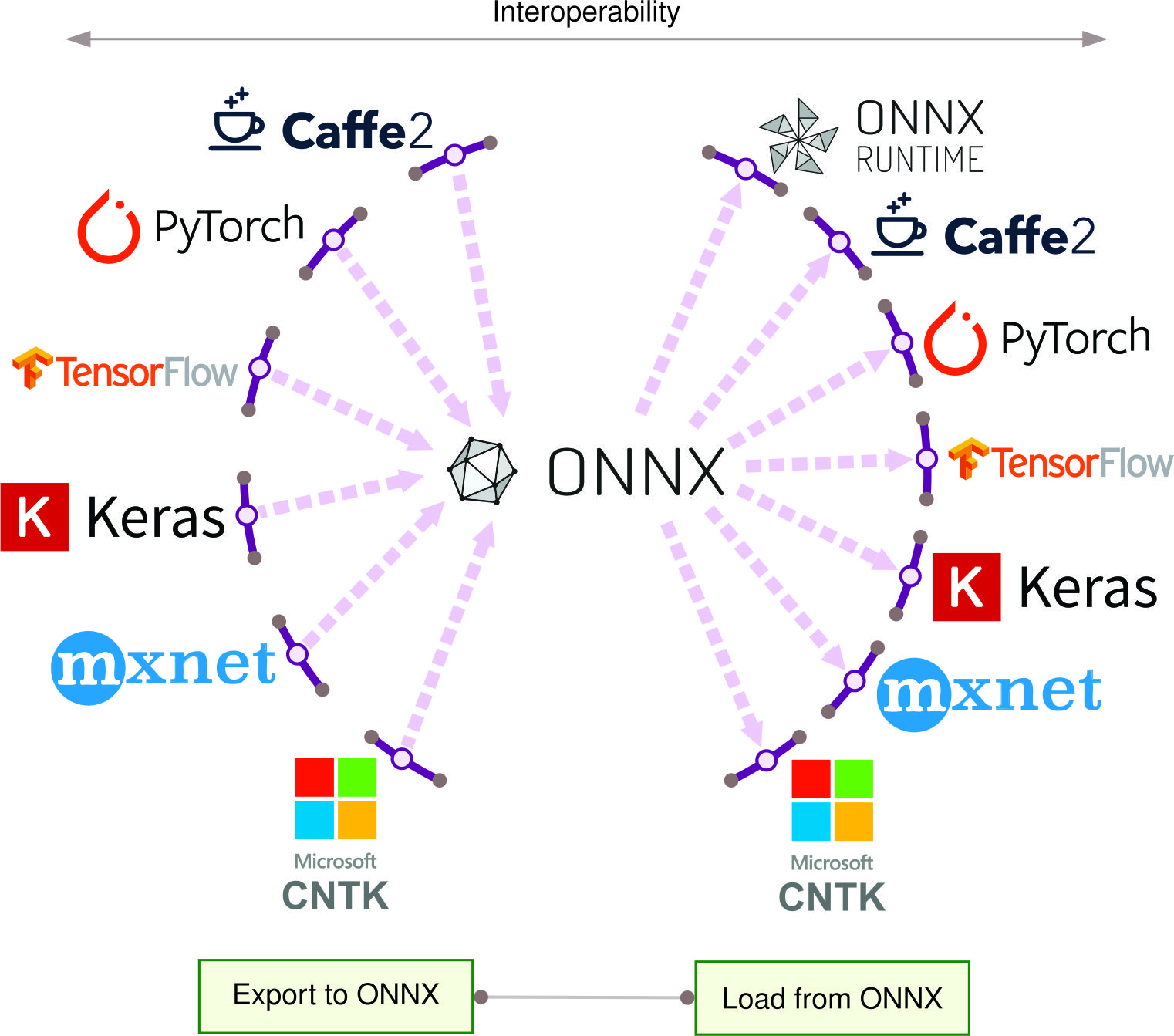
7 AI Frameworks
Resources: Slides, Videos, Exercises
Purpose
How do AI frameworks bridge the gap between theoretical design and practical implementation, and what role do they play in enabling scalable and effiicent machine learning systems?
AI frameworks are the middleware software layer that transforms abstract model specifications into executable implementations. The evolution of these frameworks reveals fundamental patterns for translating high-level designs into efficient computational workflows and system execution. Their architecture shines light on the essential trade-offs between abstraction, performance, and portability, providing systematic approaches to managing complexity in machine learning systems. Understanding framework capabilities and constraints offers insights into the engineering decisions that shape system scalability, enabling the development of robust, deployable solutions across diverse computing environments.
Trace the evolution of machine learning frameworks from early numerical libraries to modern deep learning systems
Analyze framework fundamentals including tensor data structures, computational graphs, execution models, and memory management
Differentiate between machine learning frameworks architectures, execution strategies, and development tools
Compare framework specializations across cloud, edge, mobile, and TinyML applications
7.1 Overview
Modern machine learning development relies fundamentally on machine learning frameworks, which are comprehensive software libraries or platforms designed to simplify the development, training, and deployment of machine learning models. These frameworks play multiple roles in ML systems, much like operating systems are the foundation of computing systems. Just as operating systems abstract away the complexity of hardware resources and provide standardized interfaces for applications, ML frameworks abstract the intricacies of mathematical operations and hardware acceleration, providing standardized APIs for ML development.
The capabilities of ML frameworks are diverse and continuously evolving. They provide efficient implementations of mathematical operations, automatic differentiation capabilities, and tools for managing model development, hardware acceleration, and memory utilization. For production systems, they offer standardized approaches to model deployment, versioning, and optimization. However, due to their diversity, there is no universally agreed-upon definition of an ML framework. To establish clarity for this chapter, we adopt the following definition:
A Machine Learning Framework (ML Framework) is a software platform that provides tools and abstractions for designing, training, and deploying machine learning models. It bridges user applications with infrastructure, enabling algorithmic expressiveness through computational graphs and operators, workflow orchestration across the machine learning lifecycle, hardware optimization with schedulers and compilers, scalability for distributed and edge systems, and extensibility to support diverse use cases. ML frameworks form the foundation of modern machine learning systems by simplifying development and deployment processes.
The landscape of ML frameworks continues to evolve with the field itself. Today’s frameworks must address diverse requirements: from training large language models on distributed systems to deploying compact neural networks on tiny IoT devices. Popular frameworks like PyTorch and TensorFlow have developed rich ecosystems that extend far beyond basic model implementation, encompassing tools for data preprocessing, model optimization, and deployment.
As we progress into examining training, optimization, and deployment, understanding ML frameworks becomes necessary as they orchestrate the entire machine learning lifecycle. These frameworks provide the architecture that connects all aspects of ML systems, from data ingestion to model deployment. Just as understanding a blueprint is important before studying construction techniques, grasping framework architecture is vital before diving into training methodologies and deployment strategies. Modern frameworks encapsulate the complete ML workflow, and their design choices influence how we approach training, optimization, and inference.
This chapter helps us learn how these complex frameworks function, their architectural principles, and their role in modern ML systems. Understanding these concepts will provide the necessary context as we explore specific aspects of the ML lifecycle in subsequent chapters.
7.2 Historical Evolution
The evolution of machine learning frameworks mirrors the broader development of artificial intelligence and computational capabilities. This section explores the distinct phases that reflect both technological advances and changing requirements of the AI community, from early numerical computing libraries to modern deep learning frameworks.
7.2.1 Timeline
The development of machine learning frameworks has been built upon decades of foundational work in computational libraries. From the early building blocks of BLAS and LAPACK to today’s cutting-edge frameworks like TensorFlow, PyTorch, and JAX, this journey represents a steady progression toward higher-level abstractions that make machine learning more accessible and powerful.
Looking at Figure 7.1, we can trace how these fundamental numerical computing libraries laid the groundwork for modern ML development. The mathematical foundations established by BLAS and LAPACK enabled the creation of more user-friendly tools like NumPy and SciPy, which in turn set the stage for today’s sophisticated deep learning frameworks.
This evolution reflects a clear trend: each new layer of abstraction has made complex computational tasks more approachable while building upon the robust foundations of its predecessors. Let us examine how these systems built on top of one another.
7.2.2 Early Numerical Libraries
The foundation for modern ML frameworks begins at the most fundamental level of computation: matrix operations. Machine learning computations are primarily matrix-matrix and matrix-vector multiplications. The Basic Linear Algebra Subprograms (BLAS), developed in 1979, provided these essential matrix operations that would become the computational backbone of machine learning (Kung and Leiserson 1979). These low-level operations, when combined and executed efficiently, enable the complex calculations required for training neural networks and other ML models.
Building upon BLAS, the Linear Algebra Package (LAPACK) emerged in 1992, extending these capabilities with more sophisticated linear algebra operations such as matrix decompositions, eigenvalue problems, and linear system solutions. This layered approach of building increasingly complex operations from fundamental matrix computations became a defining characteristic of ML frameworks.
The development of NumPy in 2006 marked a crucial milestone in this evolution, building upon its predecessors Numeric and Numarray to become the fundamental package for numerical computation in Python. NumPy introduced n-dimensional array objects and essential mathematical functions, but more importantly, it provided an efficient interface to these underlying BLAS and LAPACK operations. This abstraction allowed developers to work with high-level array operations while maintaining the performance of optimized low-level matrix computations.
In 2001, SciPy emerged as a powerful extension built on top of NumPy, adding specialized functions for optimization, linear algebra, and signal processing. This further exemplified the pattern of progressive abstraction in ML frameworks: from basic matrix operations to sophisticated numerical computations, and eventually to high-level machine learning algorithms. This layered architecture, starting from fundamental matrix operations and building upward, would become a blueprint for future ML frameworks, as we will see in this chapter.
7.2.3 First-Generation ML Frameworks
The transition from numerical libraries to dedicated machine learning frameworks marked a crucial evolution in abstraction. While the underlying computations remained rooted in matrix operations, frameworks began to encapsulate these operations into higher-level machine learning primitives. The University of Waikato introduced Weka in 1993 (Witten and Frank 2002), one of the earliest ML frameworks, which abstracted matrix operations into data mining tasks, though it was limited by its Java implementation and focus on smaller-scale computations.
Scikit-learn, emerging in 2007, was a significant advancement in this abstraction. Building upon the NumPy and SciPy foundation, it transformed basic matrix operations into intuitive ML algorithms. For example, what was fundamentally a series of matrix multiplications and gradient computations became a simple fit() method call in a logistic regression model. This abstraction pattern - hiding complex matrix operations behind clean APIs - would become a defining characteristic of modern ML frameworks.
Theano, which appeared in 2007, was a major advancement—developed at the Montreal Institute for Learning Algorithms (MILA)—Theano introduced two revolutionary concepts: computational graphs and GPU acceleration (Team et al. 2016). Computational graphs represented mathematical operations as directed graphs, with matrix operations as nodes and data flowing between them. This graph-based approach allowed for automatic differentiation and optimization of the underlying matrix operations. More importantly, it enabled the framework to automatically route these operations to GPU hardware, dramatically accelerating matrix computations.
Meanwhile, Torch, created at NYU in 2002, took a different approach to handling matrix operations. It emphasized immediate execution of operations (eager execution) and provided a flexible interface for neural network implementations. Torch’s design philosophy of prioritizing developer experience while maintaining high performance influenced many subsequent frameworks. Its architecture demonstrated how to balance high-level abstractions with efficient low-level matrix operations, establishing design patterns that would later influence frameworks like PyTorch.
7.2.4 Rise of Deep Learning Frameworks
The deep learning revolution demanded a fundamental shift in how frameworks handled matrix operations, primarily due to three factors: the massive scale of computations, the complexity of gradient calculations through deep networks, and the need for distributed processing. Traditional frameworks, designed for classical machine learning algorithms, could not efficiently handle the billions of matrix operations required for training deep neural networks.
The foundations for modern deep learning frameworks emerged from academic research. The University of Montreal’s Theano, released in 2007, established the concepts that would shape future frameworks (Bergstra et al. 2010). It introduced key concepts such as computational graphs1 for automatic differentiation and GPU acceleration, which we will explore in more detail later in this chapter, demonstrating how to efficiently organize and optimize complex neural network computations.
1 Computational Graph: A representation of mathematical computations as a directed graph, where nodes represent operations and edges represent data dependencies, used to enable automatic differentiation.
Caffe, released by UC Berkeley in 2013, advanced this evolution by introducing specialized implementations of convolutional operations (Jia et al. 2014). While convolutions are mathematically equivalent to specific patterns of matrix multiplication, Caffe optimized these patterns specifically for computer vision tasks, demonstrating how specialized matrix operation implementations could dramatically improve performance for specific network architectures.
Google’s TensorFlow, introduced in 2015, revolutionized the field by treating matrix operations as part of a distributed computing problem (Dean et al. 2012). It represented all computations, from individual matrix multiplications to entire neural networks, as a static computational graph that could be split across multiple devices. This approach enabled training of unprecedented model sizes by distributing matrix operations across clusters of computers and specialized hardware. TensorFlow’s static graph approach, while initially constraining, allowed for aggressive optimization of matrix operations through techniques like kernel fusion (combining multiple operations into a single kernel for efficiency) and memory planning (pre-allocating memory for operations).
Microsoft’s CNTK entered the landscape in 2016, bringing robust implementations for speech recognition and natural language processing tasks (Seide and Agarwal 2016). Its architecture emphasized scalability across distributed systems while maintaining efficient computation for sequence-based models.
Facebook’s PyTorch, also launched in 2016, took a radically different approach to handling matrix computations. Instead of static graphs, PyTorch introduced dynamic computational graphs that could be modified on the fly (Ansel et al. 2024). This dynamic approach, while potentially sacrificing some optimization opportunities, made it much easier for researchers to debug and understand the flow of matrix operations in their models. PyTorch’s success demonstrated that the ability to introspect and modify computations dynamically was as important as raw performance for many applications.
Amazon’s MXNet approached the challenge of large-scale matrix operations by focusing on memory efficiency and scalability across different hardware configurations. It introduced a hybrid approach that combined aspects of both static and dynamic graphs, allowing for flexible model development while still enabling aggressive optimization of the underlying matrix operations.
As deep learning applications grew more diverse, the need for specialized and higher-level abstractions became apparent. Keras emerged in 2015 to address this need, providing a unified interface that could run on top of multiple lower-level frameworks (Chollet et al. 2015).
Google’s JAX, introduced in 2018, brought functional programming principles to deep learning computations, enabling new patterns of model development (Bradbury et al. 2018). FastAI built upon PyTorch to package common deep learning patterns into reusable components, making advanced techniques more accessible to practitioners (Howard and Gugger 2020). These higher-level frameworks demonstrated how abstraction could simplify development while maintaining the performance benefits of their underlying implementations.
7.2.5 Hardware Influence on Design
Hardware developments have fundamentally reshaped how frameworks implement and optimize matrix operations. The introduction of NVIDIA’s CUDA platform in 2007 marked a pivotal moment in framework design by enabling general-purpose computing on GPUs. This was transformative because GPUs excel at parallel matrix operations, offering orders of magnitude speedup for the computations in deep learning. While a CPU might process matrix elements sequentially, a GPU can process thousands of elements simultaneously, fundamentally changing how frameworks approach computation scheduling.
The development of hardware-specific accelerators further revolutionized framework design. Google’s Tensor Processing Units (TPUs), first deployed in 2016, were purpose-built for tensor operations, the fundamental building blocks of deep learning computations. TPUs introduced systolic array architectures2, which are particularly efficient for matrix multiplication and convolution operations. This hardware architecture prompted frameworks like TensorFlow to develop specialized compilation strategies that could map high-level operations directly to TPU instructions, bypassing traditional CPU-oriented optimizations.
2 Systolic Array: A hardware architecture designed to perform a series of parallel computations in a time-synchronized manner, optimizing the flow of data through a grid of processors for tasks like matrix multiplication.
3 Operation fusion: A technique that combines multiple consecutive operations into a single kernel to reduce memory bandwidth usage and improve computational efficiency, particularly for element-wise operations.
Mobile hardware accelerators, such as Apple’s Neural Engine (2017) and Qualcomm’s Neural Processing Units, brought new constraints and opportunities to framework design. These devices emphasized power efficiency over raw computational speed, requiring frameworks to develop new strategies for quantization and operator fusion3. Mobile frameworks like TensorFlow Lite (more recently rebraneded to LiteRT) and PyTorch Mobile needed to balance model accuracy with energy consumption, leading to innovations in how matrix operations are scheduled and executed.
The emergence of custom ASIC (Application-Specific Integrated Circuit)4 solutions has further diversified the hardware landscape. Companies like Graphcore, Cerebras, and SambaNova have developed unique architectures for matrix computation, each with different strengths and optimization opportunities. This proliferation of specialized hardware has pushed frameworks to adopt more flexible intermediate representations of matrix operations, allowing for target-specific optimization while maintaining a common high-level interface.
4 Application-Specific Integrated Circuit (ASIC): is a custom-built hardware chip optimized for specific tasks, such as matrix computations in deep learning, offering superior performance and energy efficiency compared to general-purpose processors.
Field Programmable Gate Arrays (FPGAs) introduced yet another dimension to framework optimization. Unlike fixed-function ASICs, FPGAs allow for reconfigurable circuits that can be optimized for specific matrix operation patterns. Frameworks responding to this capability developed just-in-time compilation strategies that could generate optimized hardware configurations based on the specific needs of a model.
7.3 Framework Fundamentals
Modern machine learning frameworks operate through the integration of four key layers: Fundamentals, Data Handling, Developer Interface, and Execution and Abstraction. These layers function together to provide a structured and efficient foundation for model development and deployment, as illustrated in Figure 7.2.
The Fundamentals layer establishes the structural basis of these frameworks through computational graphs. These graphs represent the operations within a model as directed acyclic graphs (DAGs), enabling automatic differentiation and optimization. By organizing operations and data dependencies, computational graphs provide the framework with the ability to distribute workloads and execute computations efficiently across a variety of hardware platforms.
The Data Handling layer manages numerical data and parameters essential for machine learning workflows. Central to this layer are specialized data structures, such as tensors, which handle high-dimensional arrays while optimizing memory usage and device placement. Additionally, memory management and data movement strategies ensure that computational workloads are executed efficiently, particularly in environments with diverse or limited hardware resources.
The Developer Interface layer provides the tools and abstractions through which users interact with the framework. Programming models allow developers to define machine learning algorithms in a manner suited to their specific needs. These are categorized as either imperative or symbolic. Imperative models offer flexibility and ease of debugging, while symbolic models prioritize performance and deployment efficiency. Execution models further shape this interaction by defining whether computations are carried out eagerly (immediately) or as pre-optimized static graphs.
The Execution and Abstraction layer transforms these high-level representations into efficient hardware-executable operations. Core operations, encompassing everything from basic linear algebra to complex neural network layers, are highly optimized for diverse hardware platforms. This layer also includes mechanisms for allocating resources and managing memory dynamically, ensuring robust and scalable performance in both training and inference settings.
Understanding these interconnected layers is essential for leveraging machine learning frameworks effectively. Each layer plays a distinct yet interdependent role in facilitating experimentation, optimization, and deployment. By mastering these concepts, practitioners can make informed decisions about resource utilization, scaling strategies, and the suitability of specific frameworks for various tasks.
7.3.1 Computational Graphs
Machine learning frameworks must efficiently translate high-level model descriptions into executable computations across diverse hardware platforms. At the center of this translation lies the computational graph—a powerful abstraction that represents mathematical operations and their dependencies. We begin by examining the fundamental structure of computational graphs, then investigate their implementation in modern frameworks, and analyze their implications for system design and performance.
Graph Basics
Computational graphs emerged as a fundamental abstraction in machine learning frameworks to address the growing complexity of deep learning models. As models grew larger and more sophisticated, the need for efficient execution across diverse hardware platforms became crucial. The computational graph bridges the gap between high-level model descriptions and low-level hardware execution (Baydin et al. 2017), representing a machine learning model as a directed acyclic graph (DAG) where nodes represent operations and edges represent data flow.
For example, a node might represent a matrix multiplication operation, taking two input matrices (or tensors) and producing an output matrix (or tensor). To visualize this, consider the simple example in Figure 7.3. The directed acyclic graph computes \(z = x \times y\), where each variable is just numbers.
As shown in Figure 7.4, the structure of the computation graph involves defining interconnected layers, such as convolution, activation, pooling, and normalization, which are optimized before execution. The figure also demonstrates key system-level interactions, including memory management and device placement, showing how the static graph approach enables comprehensive pre-execution analysis and resource allocation.
Layers and Tensors
Modern machine learning frameworks implement neural network computations through two key abstractions: layers and tensors. Layers represent computational units that perform operations like convolution, pooling, or dense transformations. Each layer maintains internal states, including weights and biases, that evolve during model training. When data flows through these layers, it takes the form of tensors—immutable mathematical objects that hold and transmit numerical values.
The relationship between layers and tensors mirrors the distinction between operations and data in traditional programming. A layer defines how to transform input tensors into output tensors, much like a function defines how to transform its inputs into outputs. However, layers add an extra dimension: they maintain and update internal parameters during training. For example, a convolutional layer not only specifies how to perform convolution operations but also learns and stores the optimal convolution filters for a given task.
Frameworks like TensorFlow and PyTorch leverage this abstraction to simplify model implementation. When a developer writes tf.keras.layers.Conv2D, the framework constructs the necessary graph nodes for convolution operations, parameter management, and data flow. This high-level interface shields developers from the complexities of implementing convolution operations, managing memory, or handling parameter updates during training.
Building Neural Networks
The power of computational graphs extends beyond basic layer operations. Activation functions, essential for introducing non-linearity in neural networks, become nodes in the graph. Functions like ReLU, sigmoid, and tanh transform the output tensors of layers, enabling networks to approximate complex mathematical functions. Frameworks provide optimized implementations of these activation functions, allowing developers to experiment with different non-linearities without worrying about implementation details.
Modern frameworks further extend this abstraction by providing complete model architectures as pre-configured computational graphs. Models like ResNet and MobileNet, which have proven effective across many tasks, come ready to use. Developers can start with these architectures, customize specific layers for their needs, and leverage transfer learning from pre-trained weights. This approach accelerates development while maintaining the benefits of carefully optimized implementations.
System-Level Implications
The computational graph abstraction fundamentally shapes how machine learning frameworks operate. By representing computations as a directed acyclic graph, frameworks gain the ability to analyze and optimize the entire computation before execution begins. The explicit representation of data dependencies enables automatic differentiation—a crucial capability for training neural networks through gradient-based optimization.
This graph structure also provides flexibility in execution. The same model definition can run efficiently across different hardware platforms, from CPUs to GPUs to specialized accelerators. The framework handles the complexity of mapping operations to specific hardware capabilities, optimizing memory usage, and coordinating parallel execution. Moreover, the graph structure enables model serialization, allowing trained models to be saved, shared, and deployed across different environments.
While neural network diagrams help visualize model architecture, computational graphs serve a deeper purpose. They provide the precise mathematical representation needed to bridge the gap between intuitive model design and efficient execution. Understanding this representation reveals how frameworks transform high-level model descriptions into optimized, hardware-specific implementations, making modern deep learning practical at scale.
It is important to differentiate computational graphs from neural network diagrams, such as those for multilayer perceptrons (MLPs), which depict nodes and layers. Neural network diagrams visualize the architecture and flow of data through nodes and layers, providing an intuitive understanding of the model’s structure. In contrast, computational graphs provide a low-level representation of the underlying mathematical operations and data dependencies required to implement and train these networks.
From a systems perspective, computational graphs provide several key capabilities that influence the entire machine learning pipeline. They enable automatic differentiation5, which we will discuss later, provide clear structure for analyzing data dependencies and potential parallelism, and serve as an intermediate representation that can be optimized and transformed for different hardware targets. Understanding this architecture is essential for comprehending how frameworks translate high-level model descriptions into efficient executable code.
5 A computational technique that systematically computes derivatives of functions using the chain rule, crucial for training machine learning models through gradient-based optimization.
Static Graphs
Static computation graphs, pioneered by early versions of TensorFlow, implement a “define-then-run” execution model. In this approach, developers must specify the entire computation graph before execution begins. This architectural choice has significant implications for both system performance and development workflow, as we will examine later.
A static computation graph implements a clear separation between the definition of operations and their execution. During the definition phase, each mathematical operation, variable, and data flow connection is explicitly declared and added to the graph structure. This graph is a complete specification of the computation but does not perform any actual calculations. Instead, the framework constructs an internal representation of all operations and their dependencies, which will be executed in a subsequent phase.
This upfront definition enables powerful system-level optimizations. The framework can analyze the complete structure to identify opportunities for operation fusion, eliminating unnecessary intermediate results. Memory requirements can be precisely calculated and optimized in advance, leading to efficient allocation strategies. Furthermore, static graphs can be compiled into highly optimized executable code for specific hardware targets, taking full advantage of platform-specific features. Once validated, the same computation can be run repeatedly with high confidence in its behavior and performance characteristics.
Figure 7.5 illustrates this fundamental two-phase approach: first, the complete computational graph is constructed and optimized; then, during the execution phase, actual data flows through the graph to produce results. This separation enables the framework to perform comprehensive analysis and optimization of the entire computation before any execution begins.
Dynamic Graphs
Dynamic computation graphs, popularized by PyTorch, implement a “define-by-run” execution model. This approach constructs the graph during execution, offering greater flexibility in model definition and debugging. Unlike static graphs, which rely on predefined memory allocation, dynamic graphs allocate memory as operations execute, making them susceptible to memory fragmentation6 in long-running tasks.
6 Memory Fragmentation: The inefficient use of memory caused by small, unused gaps between allocated memory blocks, often resulting in wasted memory or reduced performance.
As shown in Figure 7.6, each operation is defined, executed, and completed before moving on to define the next operation. This contrasts sharply with static graphs, where all operations must be defined upfront. When an operation is defined, it is immediately executed, and its results become available for subsequent operations or for inspection during debugging. This cycle continues until all operations are complete.
Dynamic graphs excel in scenarios that require conditional execution or dynamic control flow, such as when processing variable-length sequences or implementing complex branching logic. They provide immediate feedback during development, making it easier to identify and fix issues in the computational pipeline. This flexibility aligns naturally with imperative programming patterns familiar to most developers, allowing them to inspect and modify computations at runtime. These characteristics make dynamic graphs particularly valuable during the research and development phase of ML projects.
System Implications
The architectural differences between static and dynamic computational graphs have multiple implications for how machine learning systems are designed and executed. These implications touch on various aspects of memory usage, device utilization, execution optimization, and debugging, all of which play crucial roles in determining the efficiency and scalability of a system. Here, we start with a focus on memory management and device placement as foundational concepts, leaving more detailed discussions for later chapters. This allows us to build a clear understanding before exploring more complex topics like optimization and fault tolerance.
Memory Management
Memory management occurs when executing computational graphs. Static graphs benefit from their predefined structure, allowing for precise memory planning before execution. Frameworks can calculate memory requirements in advance, optimize allocation, and minimize overhead through techniques like memory reuse. This structured approach helps ensure consistent performance, particularly in resource-constrained environments, such as Mobile and Tiny ML systems.
Dynamic graphs, by contrast, allocate memory dynamically as operations are executed. While this flexibility is invaluable for handling dynamic control flows or variable input sizes, it can result in higher memory overhead and fragmentation. These trade-offs are often most apparent during development, where dynamic graphs enable rapid iteration and debugging but may require additional optimization for production deployment.
Device Placement
Device placement, the process of assigning operations to hardware resources such as CPUs, GPUs, or specialized ASICS like TPUs, is another system-level consideration. Static graphs allow for detailed pre-execution analysis, enabling the framework to map computationally intensive operations efficiently to devices while minimizing communication overhead. This capability makes static graphs well-suited for optimizing execution on specialized hardware, where performance gains can be significant.
Dynamic graphs, in contrast, handle device placement at runtime. This allows them to adapt to changing conditions, such as hardware availability or workload demands. However, the lack of a complete graph structure before execution can make it challenging to optimize device utilization fully, potentially leading to inefficiencies in large-scale or distributed setups.
A Broader Perspective
The trade-offs between static and dynamic graphs extend well beyond memory and device considerations. As shown in Table 7.1, these architectures influence optimization potential, debugging capabilities, scalability, and deployment complexity. While these broader implications are not the focus of this section, they will be explored in detail in later chapters, particularly in the context of training workflows and system-level optimizations.
These hybrid solutions aim to provide the flexibility of dynamic graphs during development while enabling the performance optimizations of static graphs in production environments. The choice between static and dynamic graphs often depends on specific project requirements, balancing factors like development speed, production performance, and system complexity.
| Aspect | Static Graphs | Dynamic Graphs |
|---|---|---|
| Memory Management | Precise allocation planning, optimized memory usage | Flexible but potentially less efficient allocation |
| Optimization Potential | Comprehensive graph-level optimizations possible | Limited to local optimizations due to runtime construction |
| Hardware Utilization | Can generate highly optimized hardware-specific code | May sacrifice some hardware-specific optimizations |
| Development Experience | Requires more upfront planning, harder to debug | Better debugging, faster iteration cycles |
| Runtime Flexibility | Fixed computation structure | Can adapt to runtime conditions |
| Production Performance | Generally better performance at scale | May have overhead from runtime graph construction |
| Integration with Traditional Code | More separation between definition and execution | Natural integration with imperative code |
| Memory Overhead | Lower memory overhead due to planned allocations | Higher memory overhead due to dynamic allocations |
| Debugging Capability | Limited to pre-execution analysis | Runtime inspection and modification possible |
| Deployment Complexity | Simpler deployment due to fixed structure | May require additional runtime support |
7.3.2 Automatic Differentiation
Machine learning frameworks must solve a fundamental computational challenge: calculating derivatives through complex chains of mathematical operations efficiently and accurately. This capability enables the training of neural networks by computing how millions of parameters should be adjusted to improve the model’s performance.
Consider a simple computation that illustrates this challenge:
def f(x):
a = x * x # Square
b = sin(x) # Sine
return a * b # ProductEven in this basic example, computing derivatives manually would require careful application of calculus rules - the product rule, the chain rule, and derivatives of trigonometric functions. Now imagine scaling this to a neural network with millions of operations. This is where automatic differentiation (AD) becomes essential.
Automatic differentiation calculates derivatives of functions implemented as computer programs by decomposing them into elementary operations. In our example, AD breaks down f(x) into three basic steps:
- Computing
a = x * x(squaring) - Computing
b = sin(x)(sine function) - Computing the final product
a * b
For each step, AD knows the basic derivative rules:
- For squaring:
d(x²)/dx = 2x - For sine:
d(sin(x))/dx = cos(x) - For products:
d(uv)/dx = u(dv/dx) + v(du/dx)
By tracking how these operations combine and systematically applying the chain rule, AD computes exact derivatives through the entire computation. When implemented in frameworks like PyTorch or TensorFlow, this enables automatic computation of gradients through arbitrary neural network architectures.7 This fundamental understanding of how AD decomposes and tracks computations sets the foundation for examining its implementation in machine learning frameworks. We will explore its mathematical principles, system architecture implications, and performance considerations that make modern machine learning possible.
7 Automatic differentiation (AD) benefits diverse fields beyond machine learning, including physics simulations, design optimization, and financial risk analysis, by efficiently and accurately computing derivatives for complex processes.
Computational Approaches
Forward Mode
Forward mode automatic differentiation computes derivatives alongside the original computation, tracking how changes propagate from input to output. This approach mirrors how we might manually compute derivatives, making it intuitive to understand and implement in machine learning frameworks.
Consider our previous example with a slight modification to show how forward mode works:
def f(x): # Computing both value and derivative
# Step 1: x -> x²
a = x * x # Value: x²
da = 2 * x # Derivative: 2x
# Step 2: x -> sin(x)
b = sin(x) # Value: sin(x)
db = cos(x) # Derivative: cos(x)
# Step 3: Combine using product rule
result = a * b # Value: x² * sin(x)
dresult = a * db + b * da # Derivative: x²*cos(x) + sin(x)*2x
return result, dresultForward mode achieves this systematic derivative computation by augmenting each number with its derivative value, creating what mathematicians call a “dual number.” When x = 2.0, the computation tracks both values and derivatives:
x = 2.0 # Initial value
dx = 1.0 # We're tracking derivative with respect to x
# Step 1: x²
a = 4.0 # (2.0)²
da = 4.0 # 2 * 2.0
# Step 2: sin(x)
b = 0.909 # sin(2.0)
db = -0.416 # cos(2.0)
# Final result
result = 3.637 # 4.0 * 0.909
dresult = 2.805 # 4.0 * (-0.416) + 0.909 * 4.0Implementation Structure
Forward mode AD structures computations to track both values and derivatives simultaneously through programs. Consider again our simple example:
def f(x):
a = x * x
b = sin(x)
return a * b When a framework executes this function in forward mode, it augments each computation to carry two pieces of information: the value itself and how that value changes with respect to the input. This paired movement of value and derivative mirrors how we think about rates of change:
# Conceptually, each computation tracks (value, derivative)
x = (2.0, 1.0) # Input value and its derivative
a = (4.0, 4.0) # x² and its derivative 2x
b = (0.909, -0.416) # sin(x) and its derivative cos(x)
result = (3.637, 2.805) # Final value and derivativeThis forward propagation of derivative information happens automatically within the framework’s computational machinery. The framework: 1. Enriches each value with derivative information 2. Transforms each basic operation to handle both value and derivative 3. Propagates this information forward through the computation
The beauty of this approach is that it follows the natural flow of computation - as values move forward through the program, their derivatives move with them. This makes forward mode particularly well-suited for functions with single inputs and multiple outputs, as the derivative information follows the same path as the regular computation.
Performance Characteristics
Forward mode AD exhibits distinct performance patterns that influence when and how frameworks employ it. Understanding these characteristics helps explain why frameworks choose different AD approaches for different scenarios.
Forward mode performs one derivative computation alongside each original operation. For a function with one input variable, this means roughly doubling the computational work - once for the value, once for the derivative. The cost scales linearly with the number of operations in the program, making it predictable and manageable for simple computations.
However, consider a neural network layer computing derivatives for matrix multiplication between weights and inputs. To compute derivatives with respect to all weights, forward mode would need to perform the computation once for each weight parameter - potentially thousands of times. This reveals a crucial characteristic: forward mode’s efficiency depends on the number of input variables we need derivatives for.
Forward mode’s memory requirements are relatively modest. It needs to store the original value, a single derivative value, and temporary results during computation. The memory usage stays constant regardless of how complex the computation becomes. This predictable memory pattern makes forward mode particularly suitable for embedded systems with limited memory, real-time applications requiring consistent memory use, and systems where memory bandwidth is a bottleneck.
This combination of computational scaling with input variables but constant memory usage creates specific trade-offs that influence framework design decisions. Forward mode shines in scenarios with few inputs but many outputs, where its straightforward implementation and predictable resource usage outweigh the computational cost of multiple passes.
Use Cases
While forward mode automatic differentiation isn’t the primary choice for training full neural networks, it plays several important roles in modern machine learning frameworks. Its strength lies in scenarios where we need to understand how small changes in inputs affect a network’s behavior. Consider a data scientist trying to understand why their model makes certain predictions. They might want to analyze how changing a single pixel in an image or a specific feature in their data affects the model’s output:
def analyze_image_sensitivity(model, image):
# Forward mode tracks how changing one pixel
# affects the final classification
layer1 = relu(W1 @ image + b1)
layer2 = relu(W2 @ layer1 + b2)
predictions = softmax(W3 @ layer2 + b3)
return predictionsAs the computation moves through each layer, forward mode carries both values and derivatives, making it straightforward to see how input perturbations ripple through to the final prediction. For each operation, we can track exactly how small changes propagate forward.
Neural network interpretation presents another compelling application. When researchers want to generate saliency maps or attribution scores, they often need to compute how each input element influences the output:
def compute_feature_importance(model, input_features):
# Track influence of each input feature
# through the network's computation
hidden = tanh(W1 @ input_features + b1)
logits = W2 @ hidden + b2
# Forward mode efficiently computes d(logits)/d(input)
return logitsIn specialized training scenarios, particularly those involving online learning where models update on individual examples, forward mode offers advantages. The framework can track derivatives for a single example through the network efficiently, though this approach becomes less practical when dealing with batch training or updating multiple model parameters simultaneously.
Understanding these use cases helps explain why machine learning frameworks maintain forward mode capabilities alongside other differentiation strategies. While reverse mode handles the heavy lifting of full model training, forward mode provides an elegant solution for specific analytical tasks where its computational pattern matches the problem structure.
Reverse Mode
Reverse mode automatic differentiation forms the computational backbone of modern neural network training. This isn’t by accident - reverse mode’s structure perfectly matches what we need for training neural networks. During training, we have one scalar output (the loss function) and need derivatives with respect to millions of parameters (the network weights). Reverse mode is exceptionally efficient at computing exactly this pattern of derivatives.
Let’s examine a simple computation in detail:
def f(x):
a = x * x # First operation: square x
b = sin(x) # Second operation: sine of x
c = a * b # Third operation: multiply results
return cIn this function, we have three operations that create a computational chain. Notice how ‘x’ influences the final result ‘c’ through two different paths: once through squaring (a = x²) and once through sine (b = sin(x)). We’ll need to account for both paths when computing derivatives.
First, the forward pass computes and stores values:
# Forward pass - computing and storing each intermediate value
x = 2.0 # Our input value
a = 4.0 # x * x = 2.0 * 2.0 = 4.0
b = 0.909 # sin(2.0) ≈ 0.909
c = 3.637 # a * b = 4.0 * 0.909 ≈ 3.637Then comes the backward pass. This is where reverse mode shows its elegance. We start at the output and work backwards:
# Backward pass - computing derivatives in reverse
dc/dc = 1.0 # Derivative of output with respect to itself is 1
# Moving backward through multiplication c = a * b
dc/da = b # ∂(a*b)/∂a = b = 0.909
dc/db = a # ∂(a*b)/∂b = a = 4.0
# Finally, combining derivatives for x through both paths
# Path 1: x -> x² -> c contribution: 2x * dc/da
# Path 2: x -> sin(x) -> c contribution: cos(x) * dc/db
dc/dx = (2x * dc/da) + (cos(x) * dc/db)
= (2 * 2.0 * 0.909) + (cos(2.0) * 4.0)
= 3.636 + (-0.416 * 4.0)
= 2.805The power of reverse mode becomes clear when we consider what would happen if we added more operations that depend on x. Forward mode would need to track derivatives through each new path, but reverse mode efficiently handles all paths in a single backward pass. This is exactly the scenario in neural networks, where each weight can affect the final loss through multiple paths in the network.
Implementation Structure
The implementation of reverse mode in machine learning frameworks requires careful orchestration of computation and memory. While forward mode simply augments each computation, reverse mode needs to maintain a record of the forward computation to enable the backward pass. Modern frameworks accomplish this through computational graphs and automatic gradient accumulation.
Let’s extend our previous example to a small neural network computation to see how this works:
def simple_network(x, w1, w2):
# Forward pass
hidden = x * w1 # First layer multiplication
activated = max(0, hidden) # ReLU activation
output = activated * w2 # Second layer multiplication
return output # Final output (before loss)During the forward pass, the framework doesn’t just compute values - it builds a graph of operations while tracking intermediate results:
# Forward pass with value tracking
x = 1.0
w1 = 2.0
w2 = 3.0
hidden = 2.0 # x * w1 = 1.0 * 2.0
activated = 2.0 # max(0, 2.0) = 2.0
output = 6.0 # activated * w2 = 2.0 * 3.0The backward pass then uses this saved information to compute gradients for each parameter:
# Backward pass through computation
d_output = 1.0 # Start with derivative of output
d_w2 = activated # d_output * d(output)/d_w2 = 1.0 * 2.0 = 2.0
d_activated = w2 # d_output * d(output)/d_activated = 1.0 * 3.0 = 3.0
# ReLU gradient: 1 if input was > 0, 0 otherwise
d_hidden = d_activated * (1 if hidden > 0 else 0) # 3.0 * 1 = 3.0
d_w1 = x * d_hidden # 1.0 * 3.0 = 3.0
d_x = w1 * d_hidden # 2.0 * 3.0 = 6.0This example illustrates several key implementation considerations: 1. The framework must track dependencies between operations 2. Intermediate values must be stored for the backward pass 3. Gradient computations follow the reverse topological order of the forward computation 4. Each operation needs both forward and backward implementations
Memory Management Strategies
Memory management represents one of the key challenges in implementing reverse mode differentiation in machine learning frameworks. Unlike forward mode where we can discard intermediate values as we go, reverse mode requires storing results from the forward pass to compute gradients during the backward pass.
Consider our neural network example extended to show memory usage patterns:
def deep_network(x, w1, w2, w3):
# Forward pass - must store intermediates
hidden1 = x * w1
activated1 = max(0, hidden1) # Store for backward
hidden2 = activated1 * w2
activated2 = max(0, hidden2) # Store for backward
output = activated2 * w3
return outputEach intermediate value needed for gradient computation must be kept in memory until its backward pass completes. As networks grow deeper, this memory requirement grows linearly with network depth. For a typical deep neural network processing a batch of images, this can mean gigabytes of stored activations.
Frameworks employ several strategies to manage this memory burden:
# Conceptual example of memory management
def training_step(model, input_batch):
# Strategy 1: Checkpointing
with checkpoint_scope():
hidden1 = activation(layer1(input_batch))
# Framework might free some memory here
hidden2 = activation(layer2(hidden1))
# More selective memory management
output = layer3(hidden2)
# Strategy 2: Gradient accumulation
loss = compute_loss(output)
# Backward pass with managed memory
loss.backward()Modern frameworks automatically balance memory usage and computation speed. They might recompute some intermediate values during the backward pass rather than storing everything, particularly for memory-intensive operations. This trade-off between memory and computation becomes especially important in large-scale training scenarios.
Optimization Techniques
Reverse mode automatic differentiation in machine learning frameworks employs several key optimization techniques to enhance training efficiency. These optimizations become crucial when training large neural networks where computational and memory resources are pushed to their limits.
Modern frameworks implement gradient checkpointing, a technique that strategically balances computation and memory. Consider a deep neural network:
def deep_network(input_tensor):
# A typical deep network computation
layer1 = large_dense_layer(input_tensor)
activation1 = relu(layer1)
layer2 = large_dense_layer(activation1)
activation2 = relu(layer2)
# ... many more layers
output = final_layer(activation_n)
return outputInstead of storing all intermediate activations, frameworks can strategically recompute certain values during the backward pass. This trades additional computation for reduced memory usage. The framework might save activations only every few layers:
# Conceptual representation of checkpointing
checkpoint1 = save_for_backward(activation1)
# Intermediate activations can be recomputed
checkpoint2 = save_for_backward(activation4)
# Framework balances storage vs recomputationAnother crucial optimization involves operation fusion. Rather than treating each mathematical operation separately, frameworks combine operations that commonly occur together. Matrix multiplication followed by bias addition, for instance, can be fused into a single operation, reducing memory transfers and improving hardware utilization.
The backward pass itself can be optimized by reordering computations to maximize hardware efficiency. Consider the gradient computation for a convolution layer - rather than directly translating the mathematical definition into code, frameworks implement specialized backward operations that take advantage of modern hardware capabilities.
These optimizations work together to make the training of large neural networks practical. Without them, many modern architectures would be prohibitively expensive to train, both in terms of memory usage and computation time.
Framework Integration
The integration of automatic differentiation into machine learning frameworks requires careful system design to balance flexibility, performance, and usability. Modern frameworks like PyTorch and TensorFlow expose AD capabilities through high-level APIs while maintaining the sophisticated underlying machinery.
Let’s examine how frameworks present AD to users:
# PyTorch-style automatic differentiation
def neural_network(x):
# Framework transparently tracks operations
layer1 = nn.Linear(784, 256)
layer2 = nn.Linear(256, 10)
# Each operation is automatically tracked
hidden = torch.relu(layer1(x))
output = layer2(hidden)
return output
# Training loop showing AD integration
for batch_x, batch_y in data_loader:
optimizer.zero_grad() # Clear previous gradients
output = neural_network(batch_x)
loss = loss_function(output, batch_y)
# Framework handles all AD machinery
loss.backward() # Automatic backward pass
optimizer.step() # Parameter updatesWhile this code appears straightforward, it masks considerable complexity. The framework must: 1. Track all operations during the forward pass 2. Build and maintain the computational graph 3. Manage memory for intermediate values 4. Schedule gradient computations efficiently 5. Interface with hardware accelerators
This integration extends beyond basic training. Frameworks must handle complex scenarios like higher-order gradients, where we compute derivatives of derivatives, and mixed-precision training, where different parts of the computation use different numerical precisions:
# Computing higher-order gradients
with torch.set_grad_enabled(True):
# First-order gradient computation
output = model(input)
grad_output = torch.autograd.grad(output, model.parameters())
# Second-order gradient computation
grad2_output = torch.autograd.grad(grad_output, model.parameters())Memory Implications
The memory demands of automatic differentiation stem from a fundamental requirement: to compute gradients during the backward pass, we must remember what happened during the forward pass. This seemingly simple requirement creates interesting challenges for machine learning frameworks. Unlike traditional programs that can discard intermediate results as soon as they’re used, AD systems must carefully preserve computational history.
Consider what happens in a neural network’s forward pass:
def neural_network(x):
# Each operation creates values we need to remember
a = layer1(x) # Must store for backward pass
b = relu(a) # Must store input to relu
c = layer2(b) # Must store for backward pass
return cWhen this network processes data, each operation creates not just its output, but also a memory obligation. The multiplication in layer1 needs to remember its inputs because computing its gradient later will require them. Even the seemingly simple relu function must track which inputs were negative to correctly propagate gradients. As networks grow deeper, these memory requirements accumulate.
This memory challenge becomes particularly interesting with deep neural networks:
# A deeper network shows the accumulating memory needs
hidden1 = large_matrix_multiply(input, weights1)
activated1 = relu(hidden1)
hidden2 = large_matrix_multiply(activated1, weights2)
activated2 = relu(hidden2)
output = large_matrix_multiply(activated2, weights3)Each layer’s computation adds to our memory burden. The framework must keep hidden1 in memory until we’ve computed gradients through hidden2, but after that, we can safely discard it. This creates a wave of memory usage that peaks when we start the backward pass and gradually recedes as we compute gradients.
Modern frameworks handle this memory choreography automatically. They track the lifetime of each intermediate value - how long it must remain in memory for gradient computation. When training large models, this careful memory management becomes as crucial as the numerical computations themselves. The framework frees memory as soon as it’s no longer needed for gradient computation, ensuring that our memory usage, while necessarily large, remains as efficient as possible.
System Considerations
Automatic differentiation’s integration into machine learning frameworks raises important system-level considerations that affect both framework design and training performance. These considerations become particularly apparent when training large neural networks where efficiency at every level matters.
Consider a typical training loop that highlights these system-level interactions:
def train_epoch(model, data_loader):
for batch_x, batch_y in data_loader:
# Moving data between CPU and accelerator
batch_x = batch_x.to(device)
batch_y = batch_y.to(device)
# Forward pass builds computational graph
outputs = model(batch_x)
loss = criterion(outputs, batch_y)
# Backward pass computes gradients
loss.backward()
optimizer.step()
optimizer.zero_grad()This simple loop masks complex system interactions. The AD system must coordinate with multiple framework components: the memory allocator, the device manager, the operation scheduler, and the optimizer. Each gradient computation potentially triggers data movement between devices, memory allocation, and kernel launches on accelerators.
The scheduling of AD operations becomes particularly intricate with modern hardware accelerators:
# Complex model with parallel computations
def parallel_network(x):
# These operations could run concurrently
branch1 = conv_layer1(x)
branch2 = conv_layer2(x)
# Must synchronize for combination
combined = branch1 + branch2
return final_layer(combined)The AD system must track dependencies not just for correct gradient computation, but also for efficient hardware utilization. It needs to determine which gradient computations can run in parallel and which must wait for others to complete. This dependency tracking extends across both forward and backward passes, creating a complex scheduling problem.
Modern frameworks handle these system-level concerns while maintaining a simple interface for users. Behind the scenes, they make sophisticated decisions about operation scheduling, memory allocation, and data movement, all while ensuring correct gradient computation through the computational graph.
Summary
Automatic differentiation systems represent an important computational abstraction in machine learning frameworks, transforming the mathematical concept of derivatives into efficient implementations. Through our examination of both forward and reverse modes, we’ve seen how frameworks balance mathematical precision with computational efficiency to enable training of modern neural networks.
The implementation of AD systems reveals key design patterns in machine learning frameworks:
# Simple computation showing AD machinery
def computation(x, w):
# Framework tracks operations
hidden = x * w # Stored for backward pass
output = relu(hidden) # Tracks activation pattern
return outputThis simple computation embodies several fundamental concepts:
- Operation tracking for derivative computation
- Memory management for intermediate values
- System coordination for efficient execution
Modern frameworks abstract these complexities behind clean interfaces while maintaining high performance:
# Framework hides AD complexity
loss = model(input) # Forward pass tracks computation
loss.backward() # Triggers efficient reverse mode AD
optimizer.step() # Uses computed gradientsThe effectiveness of automatic differentiation systems stems from their careful balance of competing demands. They must maintain sufficient computational history for accurate gradients while managing memory constraints, schedule operations efficiently while preserving correctness, and provide flexibility while optimizing performance.
Understanding these systems proves essential for both framework developers and practitioners. Framework developers must implement efficient AD to enable modern deep learning, while practitioners benefit from understanding AD’s capabilities and constraints when designing and training models.
While automatic differentiation provides the computational foundation for gradient-based learning, its practical implementation depends heavily on how frameworks organize and manipulate data. This brings us to our next topic: the data structures that enable efficient computation and memory management in machine learning frameworks. These structures must not only support AD operations but also provide efficient access patterns for the diverse hardware platforms that power modern machine learning.
Looking Forward
The automatic differentiation systems we’ve explored provide the computational foundation for neural network training, but they don’t operate in isolation. These systems need efficient ways to represent and manipulate the data flowing through them. This brings us to our next topic: the data structures that machine learning frameworks use to organize and process information.
Consider how our earlier examples handled numerical values:
def neural_network(x):
hidden = w1 * x # What exactly is x?
activated = relu(hidden) # How is hidden stored?
output = w2 * activated # What type of multiplication?
return outputThese operations appear straightforward, but they raise important questions. How do frameworks represent these values? How do they organize data to enable efficient computation and automatic differentiation? Most importantly, how do they structure data to take advantage of modern hardware?
The next section examines how frameworks answer these questions through specialized data structures, particularly tensors, that form the basic building blocks of machine learning computations.
7.3.3 Data Structures
Machine learning frameworks extend computational graphs with specialized data structures, bridging high-level computations with practical implementations. These data structures have two essential purposes: they provide containers for the numerical data that powers machine learning models, and they manage how this data is stored and moved across different memory spaces and devices.
While computational graphs specify the logical flow of operations, data structures determine how these operations actually access and manipulate data in memory. This dual role of organizing numerical data for model computations while handling the complexities of memory management and device placement shapes how frameworks translate mathematical operations into efficient executions across diverse computing platforms.
The effectiveness of machine learning frameworks depends heavily on their underlying data organization. While machine learning theory can be expressed through mathematical equations, turning these equations into practical implementations demands thoughtful consideration of data organization, storage, and manipulation. Modern machine learning models must process enormous amounts of data during training and inference, making efficient data access and memory usage critical across diverse hardware platforms.
A framework’s data structures must excel in three key areas. First, they need to deliver high performance, supporting rapid data access and efficient memory use across different hardware. This includes optimizing memory layouts for cache efficiency and enabling smooth data transfer between memory hierarchies and devices. Second, they must offer flexibility, accommodating various model architectures and training approaches while supporting different data types and precision requirements. Third, they should provide clear and intuitive interfaces to developers while handling complex memory management and device placement behind the scenes.
These data structures bridge mathematical concepts and practical computing systems. The operations in machine learning—matrix multiplication, convolution, activation functions—set basic requirements for how data must be organized. These structures must maintain numerical precision and stability while enabling efficient implementation of common operations and automatic gradient computation. However, they must also work within real-world computing constraints, dealing with limited memory bandwidth, varying hardware capabilities, and the needs of distributed computing.
The design choices made in implementing these data structures significantly influence what machine learning frameworks can achieve. Poor decisions in data structure design can result in excessive memory use, limiting model size and batch capabilities. They might create performance bottlenecks that slow down training and inference, or produce interfaces that make programming error-prone. On the other hand, thoughtful design enables automatic optimization of memory usage and computation, efficient scaling across hardware configurations, and intuitive programming interfaces that support rapid implementation of new techniques.
As we explore specific data structures in the following sections, we’ll examine how frameworks address these challenges through careful design decisions and optimization approaches. This understanding proves essential for anyone working with machine learning systems, whether developing new models, optimizing existing ones, or creating new framework capabilities. We begin with tensor abstractions, the fundamental building blocks of modern machine learning frameworks, before exploring more specialized structures for parameter management, dataset handling, and execution control.
Tensors
Machine learning frameworks process and store numerical data as tensors. Every computation in a neural network, from processing input data to updating model weights, operates on tensors. Training batches of images, activation maps in convolutional networks, and parameter gradients during backpropagation all take the form of tensors. This unified representation allows frameworks to implement consistent interfaces for data manipulation and optimize operations across different hardware architectures.
Structure and Dimensionality
A tensor is a mathematical object that generalizes scalars, vectors, and matrices to higher dimensions. The dimensionality forms a natural hierarchy: a scalar is a zero-dimensional tensor containing a single value, a vector is a one-dimensional tensor containing a sequence of values, and a matrix is a two-dimensional tensor containing values arranged in rows and columns. Higher-dimensional tensors extend this pattern through nested structures; for instance, as illustrated in Figure 7.7, a three-dimensional tensor can be visualized as a stack of matrices. Therefore, vectors and matrices can be considered special cases of tensors with 1D and 2D dimensions, respectively.
In practical applications, tensors naturally arise when dealing with complex data structures. As illustrated in Figure 7.8, image data exemplifies this concept particularly well. Color images comprise three channels, where each channel represents the intensity values of red, green, or blue as a distinct matrix. These channels combine to create the full colored image, forming a natural 3D tensor structure. When processing multiple images simultaneously, such as in batch operations, a fourth dimension can be added to create a 4D tensor, where each slice represents a complete three-channel image. This hierarchical organization demonstrates how tensors efficiently handle multidimensional data while maintaining clear structural relationships.
In machine learning frameworks, tensors take on additional properties beyond their mathematical definition to meet the demands of modern ML systems. While mathematical tensors provide a foundation as multi-dimensional arrays with transformation properties, machine learning introduces requirements for practical computation. These requirements shape how frameworks balance mathematical precision with computational performance.
Framework tensors combine numerical data arrays with computational metadata. The dimensional structure, or shape, ranges from simple vectors and matrices to higher-dimensional arrays that represent complex data like image batches or sequence models. This dimensional information plays a critical role in operation validation and optimization. Matrix multiplication operations, for example, depend on shape metadata to verify dimensional compatibility and determine optimal computation paths.
Memory layout implementation introduces distinct challenges in tensor design. While tensors provide an abstraction of multi-dimensional data, physical computer memory remains linear. Stride patterns address this disparity by creating mappings between multi-dimensional tensor indices and linear memory addresses. These patterns significantly impact computational performance by determining memory access patterns during tensor operations. Careful alignment of stride patterns with hardware memory hierarchies maximizes cache efficiency and memory throughput.
Type Systems and Precision
Tensor implementations use type systems to control numerical precision and memory consumption. The standard choice in machine learning has been 32-bit floating-point numbers (float32), offering a balance of precision and efficiency. Modern frameworks extend this with multiple numeric types for different needs. Integer types support indexing and embedding operations. Reduced-precision types like 16-bit floating-point numbers enable efficient mobile deployment. 8-bit integers allow fast inference on specialized hardware.
The choice of numeric type affects both model behavior and computational efficiency. Neural network training typically requires float32 precision to maintain stable gradient computations. Inference tasks can often use lower precision (int8 or even int4), reducing memory usage and increasing processing speed. Mixed-precision training8 approaches combine these benefits by using float32 for critical accumulations while performing most computations at lower precision.
8 Mixed-precision training: A training approach that uses lower-precision arithmetic for most calculations while retaining higher-precision for critical operations, balancing performance and numerical stability.
Type conversions between different numeric representations require careful management. Operating on tensors with different types demands explicit conversion rules to preserve numerical correctness. These conversions introduce computational costs and risk precision loss. Frameworks provide type casting capabilities but rely on developers to maintain numerical precision across operations.
Device Placement and Memory Management
The rise of heterogeneous computing has transformed how machine learning frameworks manage tensor operations. Modern frameworks must seamlessly operate across CPUs, GPUs, TPUs, and various other accelerators, each offering different computational advantages and memory characteristics. This diversity creates a fundamental challenge: tensors must move efficiently between devices while maintaining computational coherency throughout the execution of machine learning workloads.
Device placement decisions significantly influence both computational performance and memory utilization. Moving tensors between devices introduces latency costs and consumes precious bandwidth on system interconnects. Keeping multiple copies of tensors across different devices can accelerate computation by reducing data movement, but this strategy increases overall memory consumption and requires careful management of consistency between copies. Frameworks must therefore implement sophisticated memory management systems that track tensor locations and orchestrate data movement while considering these tradeoffs.
These memory management systems maintain a dynamic view of available device memory and implement strategies for efficient data transfer. When operations require tensors that reside on different devices, the framework must either move data or redistribute computation. This decision process integrates deeply with the framework’s computational graph execution and operation scheduling. Memory pressure on individual devices, data transfer costs, and computational load all factor into placement decisions.
The interplay between device placement and memory management extends beyond simple data movement. Frameworks must anticipate future computational needs to prefetch data efficiently, manage memory fragmentation across devices, and handle cases where memory demands exceed device capabilities. This requires close coordination between the memory management system and the operation scheduler, especially in scenarios involving parallel computation across multiple devices or distributed training across machine boundaries.
Specialized Structures
While tensors are the building blocks of machine learning frameworks, they are not the only structures required for effective system operation. Frameworks rely on a suite of specialized data structures tailored to address the distinct needs of data processing, model parameter management, and execution coordination. These structures ensure that the entire workflow—from raw data ingestion to optimized execution on hardware—proceeds seamlessly and efficiently.
Dataset Structures
Dataset structures handle the critical task of transforming raw input data into a format suitable for machine learning computations. These structures bridge the gap between diverse data sources and the tensor abstractions required by models, automating the process of reading, parsing, and preprocessing data.
Dataset structures must support efficient memory usage while dealing with input data far larger than what can fit into memory at once. For example, when training on large image datasets, these structures load images from disk, decode them into tensor-compatible formats, and apply transformations like normalization or augmentation in real time. Frameworks implement mechanisms such as data streaming, caching, and shuffling to ensure a steady supply of preprocessed batches without bottlenecks.
The design of dataset structures directly impacts training performance. Poorly designed structures can create significant overhead, limiting data throughput to GPUs or other accelerators. In contrast, well-optimized dataset handling can leverage parallelism across CPU cores, disk I/O, and memory transfers to feed accelerators at full capacity.
In large, multi-system distributed training scenarios, dataset structures also handle coordination between nodes, ensuring that each worker processes a distinct subset of data while maintaining consistency in operations like shuffling. This coordination prevents redundant computation and supports scalability across multiple devices and machines.
Parameter Structures
Parameter structures store the numerical values that define a machine learning model. These include the weights and biases of neural network layers, along with auxiliary data such as batch normalization statistics and optimizer state. Unlike datasets, which are transient, parameters persist throughout the lifecycle of model training and inference.
The design of parameter structures must balance efficient storage with rapid access during computation. For example, convolutional neural networks require parameters for filters, fully connected layers, and normalization layers, each with unique shapes and memory alignment requirements. Frameworks organize these parameters into compact representations that minimize memory consumption while enabling fast read and write operations.
A key challenge for parameter structures is managing memory efficiently across multiple devices (0003 et al. 2014). During distributed training, frameworks may replicate parameters across GPUs for parallel computation while keeping a synchronized master copy on the CPU. This strategy ensures consistency while reducing the latency of gradient updates. Additionally, parameter structures often leverage memory sharing techniques to minimize duplication, such as storing gradients and optimizer states in place to conserve memory.
Parameter structures must also adapt to various precision requirements. While training typically uses 32-bit floating-point precision for stability, reduced precision such as 16-bit floating-point or even 8-bit integers is increasingly used for inference and large-scale training. Frameworks implement type casting and mixed-precision management to enable these optimizations without compromising numerical accuracy.
Execution Structures
Execution structures coordinate how computations are performed on hardware, ensuring that operations execute efficiently while respecting device constraints. These structures work closely with computational graphs, determining how data flows through the system and how memory is allocated for intermediate results.
One of the primary roles of execution structures is memory management. During training or inference, intermediate computations such as activation maps or gradients can consume significant memory. Execution structures dynamically allocate and deallocate memory buffers to avoid fragmentation and maximize hardware utilization. For example, a deep neural network might reuse memory allocated for activation maps across layers, reducing the overall memory footprint.
These structures also handle operation scheduling, ensuring that computations are performed in the correct order and with optimal hardware utilization. On GPUs, for instance, execution structures can overlap computation and data transfer operations, hiding latency and improving throughput. When running on multiple devices, they synchronize dependent computations to maintain consistency without unnecessary delays.
Distributed training introduces additional complexity, as execution structures must manage data and computation across multiple nodes. This includes partitioning computational graphs, synchronizing gradients, and redistributing data as needed. Efficient execution structures minimize communication overhead, allowing distributed systems to scale linearly with additional hardware (McMahan et al. 2017).
7.3.4 Programming Models
Programming models define how developers express computations in code. In previous sections, we explored computational graphs and specialized data structures, which together define the computational processes of machine learning frameworks. Computational graphs outline the sequence of operations, such as matrix multiplication or convolution, while data structures like tensors store the numerical values that these operations manipulate. These models fall into two categories: symbolic programming and imperative programming.
Symbolic Programming
Symbolic programming involves constructing abstract representations of computations first and executing them later. This approach aligns naturally with static computational graphs, where the entire structure is defined before any computation occurs.
For instance, in symbolic programming, variables and operations are represented as symbols. These symbolic expressions are not evaluated until explicitly executed, allowing the framework to analyze and optimize the computation graph before running it.
Consider the following symbolic programming example:
# Expressions are constructed but not evaluated
weights = tf.Variable(tf.random.normal([784, 10]))
input = tf.placeholder(tf.float32, [None, 784])
output = tf.matmul(input, weights)
# Separate evaluation phase
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
result = sess.run(output, feed_dict={input: data})This approach enables frameworks to apply global optimizations across the entire computation, making it efficient for deployment scenarios. Additionally, static graphs can be serialized and executed across different environments, enhancing portability. Predefined graphs also facilitate efficient parallel execution strategies. However, debugging can be challenging because errors often surface during execution rather than graph construction, and modifying a static graph dynamically is cumbersome.
Imperative Programming
Imperative programming takes a more traditional approach, executing operations immediately as they are encountered. This method corresponds to dynamic computational graphs, where the structure evolves dynamically during execution.
In this programming paradigm, computations are performed directly as the code executes, closely resembling the procedural style of most general-purpose programming languages. For example:
# Imperative Programming Example
# Each expression evaluates immediately
weights = torch.randn(784, 10)
input = torch.randn(32, 784)
output = input @ weights # Computation occurs nowThe immediate execution model is intuitive and aligns with common programming practices, making it easier to use. Errors can be detected and resolved immediately during execution, simplifying debugging. Dynamic graphs allow for adjustments on-the-fly, making them ideal for tasks requiring variable graph structures, such as reinforcement learning or sequence modeling. However, the creation of dynamic graphs at runtime can introduce computational overhead, and the framework’s ability to optimize the entire computation graph is limited due to the step-by-step execution process.
System Implementation Considerations
The choice between symbolic and imperative programming models fundamentally influences how ML frameworks manage system-level features such as memory management and optimization strategies.
Performance Trade-offs
In symbolic programming, frameworks can analyze the entire computation graph upfront. This allows for efficient memory allocation strategies. For example, memory can be reused for intermediate results that are no longer needed during later stages of computation. This global view also enables advanced optimization techniques such as operation fusion, automatic differentiation, and hardware-specific kernel selection. These optimizations make symbolic programming highly effective for production environments where performance is critical.
In contrast, imperative programming makes memory management and optimization more challenging since decisions must be made at runtime. Each operation executes immediately, which prevents the framework from globally analyzing the computation. This trade-off, however, provides developers with greater flexibility and immediate feedback during development. Beyond system-level features, the choice of programming model also impacts the developer experience, particularly during model development and debugging.
Development and Debugging
Symbolic programming requires developers to conceptualize their models as complete computational graphs. This often involves extra steps to inspect intermediate values, as symbolic execution defers computation until explicitly invoked. For example, in TensorFlow 1.x, developers need to use sessions and feed dictionaries to debug intermediate results, which can slow down the development process.
Imperative programming offers a more straightforward debugging experience. Operations execute immediately, allowing developers to inspect tensor values and shapes as the code runs. This immediate feedback simplifies experimentation and makes it easier to identify and fix issues in the model. As a result, imperative programming is well-suited for rapid prototyping and iterative model development.
7.3.5 Execution Models
Machine learning frameworks employ various execution paradigms to determine how computations are performed. These paradigms significantly influence the development experience, performance characteristics, and deployment options of ML systems. Understanding the trade-offs between execution models is essential for selecting the right approach for a given application. Let’s explore three key execution paradigms: eager execution, graph execution, and just-in-time (JIT) compilation.
Eager Execution
Eager execution is the most straightforward and intuitive execution paradigm. In this model, operations are executed immediately as they are called in the code. This approach closely mirrors the way traditional imperative programming languages work, making it familiar to many developers.
Consider the following example using TensorFlow 2.x, which employs eager execution by default:
import tensorflow as tf
x = tf.constant([[1., 2.], [3., 4.]])
y = tf.constant([[1, 2], [3, 4]])
z = tf.matmul(x, y)
print(z)In this code snippet, each line is executed sequentially. When we create the tensors x and y, they are immediately instantiated in memory. The matrix multiplication tf.matmul(x, y) is computed right away, and the result is stored in z. When we print z, we see the output of the computation immediately.
Eager execution offers several advantages. It provides immediate feedback, allowing developers to inspect intermediate values easily. This makes debugging more straightforward and intuitive. It also allows for more dynamic and flexible code structures, as the computation graph can change with each execution.
However, eager execution has its trade-offs. Since operations are executed immediately, the framework has less opportunity to optimize the overall computation graph. This can lead to lower performance compared to more optimized execution paradigms, especially for complex models or when dealing with large datasets.
Eager execution is particularly well-suited for research, interactive development, and rapid prototyping. It allows data scientists and researchers to quickly iterate on their ideas and see results immediately. Many modern ML frameworks, including TensorFlow 2.x and PyTorch, use eager execution as their default mode due to its developer-friendly nature.
Graph Execution
Graph execution, also known as static graph execution, takes a different approach to computing operations in ML frameworks. In this paradigm, developers first define the entire computational graph, and then execute it as a separate step.
Consider the following example using TensorFlow 1.x style, which employs graph execution:
import tensorflow.compat.v1 as tf
tf.disable_eager_execution()
# Define the graph
x = tf.placeholder(tf.float32, shape=(2, 2))
y = tf.placeholder(tf.float32, shape=(2, 2))
z = tf.matmul(x, y)
# Execute the graph
with tf.Session() as sess:
result = sess.run(z, feed_dict={
x: [[1., 2.], [3., 4.]],
y: [[1, 2], [3, 4]]
})
print(result)In this code snippet, we first define the structure of our computation. The placeholder operations create nodes in the graph for input data, while tf.matmul creates a node representing matrix multiplication. Importantly, no actual computation occurs during this definition phase.
The execution of the graph happens when we create a session and call sess.run(). At this point, we provide the actual input data through the feed_dict parameter. The framework then has the complete graph and can perform optimizations before running the computation.
Graph execution offers several advantages. It allows the framework to see the entire computation ahead of time, enabling global optimizations that can improve performance, especially for complex models. Once defined, the graph can be easily saved and deployed across different environments, enhancing portability. It’s particularly efficient for scenarios where the same computation is repeated many times with different data inputs.
However, graph execution also has its trade-offs. It requires developers to think in terms of building a graph rather than writing sequential operations, which can be less intuitive. Debugging can be more challenging because errors often don’t appear until the graph is executed. Additionally, implementing dynamic computations can be more difficult with a static graph.
Graph execution is well-suited for production environments where performance and deployment consistency are crucial. It is commonly used in scenarios involving large-scale distributed training and when deploying models for predictions in high-throughput applications.
Just-In-Time Compilation
Just-In-Time (JIT) compilation is a middle ground between eager execution and graph execution. This paradigm aims to combine the flexibility of eager execution with the performance benefits of graph optimization.
Let’s examine an example using PyTorch’s JIT compilation:
import torch
@torch.jit.script
def compute(x, y):
return torch.matmul(x, y)
x = torch.randn(2, 2)
y = torch.randn(2, 2)
# First call compiles the function
result = compute(x, y)
print(result)
# Subsequent calls use the optimized version
result = compute(x, y)
print(result)In this code snippet, we define a function compute and decorate it with @torch.jit.script. This decorator tells PyTorch to compile the function using its JIT compiler. The first time compute is called, PyTorch analyzes the function, optimizes it, and generates efficient machine code. This compilation process occurs just before the function is executed, hence the term “Just-In-Time”.
Subsequent calls to compute use the optimized version, potentially offering significant performance improvements, especially for complex operations or when called repeatedly.
JIT compilation provides a balance between development flexibility and runtime performance. It allows developers to write code in a natural, eager-style manner while still benefiting from many of the optimizations typically associated with graph execution.
This approach offers several advantages. It maintains the immediate feedback and intuitive debugging of eager execution, as most of the code still executes eagerly. At the same time, it can deliver performance improvements for critical parts of the computation. JIT compilation can also adapt to the specific data types and shapes being used, potentially resulting in more efficient code than static graph compilation.
However, JIT compilation also has some considerations. The first execution of a compiled function may be slower due to the overhead of the compilation process. Additionally, some complex Python constructs may not be easily JIT-compiled, requiring developers to be aware of what can be optimized effectively.
JIT compilation is particularly useful in scenarios where you need both the flexibility of eager execution for development and prototyping, and the performance benefits of compilation for production or large-scale training. It’s commonly used in research settings where rapid iteration is necessary but performance is still a concern.
Many modern ML frameworks incorporate JIT compilation to provide developers with a balance of ease-of-use and performance optimization, as shown in Table 7.2. This balance manifests across multiple dimensions, from the learning curve that gradually introduces optimization concepts to the runtime behavior that combines immediate feedback with performance enhancements. The table highlights how JIT compilation bridges the gap between eager execution’s programming simplicity and graph execution’s performance benefits, particularly in areas like memory usage and optimization scope.
| Aspect | Eager Execution | Graph Execution | JIT Compilation |
|---|---|---|---|
| Approach | Computes each operation immediately when encountered | Builds entire computation plan first, then executes | Analyzes code at runtime, creates optimized version |
| Memory Usage | Holds intermediate results throughout computation | Optimizes memory by planning complete data flow | Adapts memory usage based on actual execution patterns |
| Optimization Scope | Limited to local operation patterns | Global optimization across entire computation chain | Combines runtime analysis with targeted optimizations |
| Debugging Approach | Examine values at any point during computation | Must set up specific monitoring points in graph | Initial runs show original behavior, then optimizes |
| Speed vs Flexibility | Prioritizes flexibility over speed | Prioritizes performance over flexibility | Balances flexibility and performance |
7.3.6 Core Operations
Machine learning frameworks employ multiple layers of operations that translate high-level model descriptions into efficient computations on hardware. These operations form a hierarchy: hardware abstraction operations manage the complexity of diverse computing platforms, basic numerical operations implement fundamental mathematical computations, and system-level operations coordinate resources and execution. This operational hierarchy is key to understanding how frameworks transform mathematical models into practical implementations. Figure 7.9 illustrates this hierarchy, showing the relationship between the three layers and their respective subcomponents.
Hardware Abstraction Operations
At the lowest level, hardware abstraction operations provide the foundation for executing computations across diverse computing platforms. These operations isolate higher layers from hardware-specific details while maintaining computational efficiency. The abstraction layer must handle three fundamental aspects: compute kernel management, memory system abstraction, and execution control.
Compute Kernel Management
Compute kernel management involves selecting and dispatching optimal implementations of mathematical operations for different hardware architectures. This requires maintaining multiple implementations of core operations and sophisticated dispatch logic. For example, a matrix multiplication operation might be implemented using AVX-5129 vector instructions on modern CPUs, cuBLAS on NVIDIA GPUs, or specialized tensor processing instructions on AI accelerators. The kernel manager must consider input sizes, data layout, and hardware capabilities when selecting implementations. It must also handle fallback paths for when specialized implementations are unavailable or unsuitable.
9 A set of 512-bit single-instruction, multiple-data (SIMD) extensions to the x86 instruction set architecture.
Memory System Abstraction
Memory system abstractions manage data movement through complex memory hierarchies. These abstractions must handle various memory types (registered, pinned, unified) and their specific access patterns. Data layouts often require transformation between hardware-preferred formats - for instance, between row-major and column-major matrix layouts, or between interleaved and planar image formats. The memory system must also manage alignment requirements, which can vary from 4-byte alignment on CPUs to 128-byte alignment on some accelerators. Additionally, it handles cache coherency issues when multiple execution units access the same data.
Execution Control
Execution control operations coordinate computation across multiple execution units and memory spaces. This includes managing execution queues, handling event dependencies, and controlling asynchronous operations. Modern hardware often supports multiple execution streams that can operate concurrently. For example, independent GPU streams or CPU thread pools. The execution controller must manage these streams, handle synchronization points, and ensure correct ordering of dependent operations. It must also provide error handling and recovery mechanisms for hardware-specific failures.
Basic Numerical Operations
Building upon hardware abstractions, frameworks implement fundamental numerical operations that form the building blocks of machine learning computations. These operations must balance mathematical precision with computational efficiency. General Matrix Multiply (GEMM) operations, which dominate the computational cost of most machine learning workloads. GEMM operations follow the pattern C = αAB + βC, where A, B, and C are matrices, and α and β are scaling factors.
The implementation of GEMM operations requires sophisticated optimization techniques. These include blocking10 for cache efficiency, where matrices are divided into smaller tiles that fit in cache memory; loop unrolling11 to increase instruction-level parallelism; and specialized implementations for different matrix shapes and sparsity patterns. For example, fully-connected neural network layers typically use regular dense GEMM operations, while convolutional layers often employ specialized GEMM variants that exploit input locality patterns.
10 An optimization technique where computations are performed on submatrices (tiles) that fit into cache memory, reducing memory access overhead and improving computational efficiency.
11 A method of increasing instruction-level parallelism by manually replicating loop iterations in the code, reducing branching overhead and enabling better utilization of CPU pipelines.
Beyond GEMM, frameworks must efficiently implement BLAS operations such as vector addition (AXPY), matrix-vector multiplication (GEMV), and various reduction operations. These operations require different optimization strategies. AXPY operations are typically memory-bandwidth limited, while GEMV operations must balance memory access patterns with computational efficiency.
Element-wise operations form another critical category, including both basic arithmetic operations (addition, multiplication) and transcendental functions (exponential, logarithm, trigonometric functions). While conceptually simpler than GEMM, these operations present significant optimization opportunities through vectorization and operation fusion. For example, multiple element-wise operations can often be fused into a single kernel to reduce memory bandwidth requirements. The efficiency of these operations becomes particularly important in neural network activation functions and normalization layers, where they process large volumes of data.
Modern frameworks must also handle operations with varying numerical precision requirements. For example, training often requires 32-bit floating-point precision for numerical stability, while inference can often use reduced precision formats like 16-bit floating-point or even 8-bit integers. Frameworks must therefore provide efficient implementations across multiple numerical formats while maintaining acceptable accuracy.
System-Level Operations
System-level operations build upon the previously discussed computational graph abstractions, hardware abstractions, and numerical operations to manage overall computation flow and resource utilization. These operations handle three critical aspects: operation scheduling, memory management, and resource optimization.
Operation scheduling leverages the computational graph structure discussed earlier to determine execution ordering. Building on the static or dynamic graph representation, the scheduler must identify parallelization opportunities while respecting dependencies. The implementation challenges differ between static graphs, where the entire dependency structure is known in advance, and dynamic graphs, where dependencies emerge during execution. The scheduler must also handle advanced execution patterns like conditional operations and loops that create dynamic control flow within the graph structure.
Memory management implements sophisticated strategies for allocating and deallocating memory resources across the computational graph. Different data types require different management strategies. Model parameters typically persist throughout execution and may require specific memory types for efficient access. Intermediate results have bounded lifetimes defined by the operation graph - for example, activation values needed only during the backward pass. The memory manager employs techniques like reference counting for automatic cleanup, memory pooling to reduce allocation overhead, and workspace management for temporary buffers. It must also handle memory fragmentation, particularly in long-running training sessions where allocation patterns can change over time.
Resource optimization integrates scheduling and memory decisions to maximize performance within system constraints. A key optimization is gradient checkpointing12, where some intermediate results are discarded and recomputed rather than stored, trading computation time for memory savings. The optimizer must also manage concurrent execution streams, balancing load across available compute units while respecting dependencies. For operations with multiple possible implementations, it selects between alternatives based on runtime conditions - for instance, choosing between matrix multiplication algorithms based on matrix shapes and system load.
12 Gradient checkpointing: A memory-saving optimization technique that stores a limited set of intermediate activations during the forward pass and recomputes the others during the backward pass to reduce memory usage.
Together, these operational layers build upon the computational graph foundation to execute machine learning workloads efficiently while abstracting implementation complexity from model developers. The interaction between these layers determines overall system performance and sets the foundation for advanced optimization techniques discussed in subsequent chapters.
7.4 Framework Components
Machine learning frameworks organize their fundamental capabilities into distinct components that work together to provide a complete development and deployment environment. These components create layers of abstraction that make frameworks both usable for high-level model development and efficient for low-level execution. Understanding how these components interact helps developers choose and use frameworks effectively.
7.4.1 APIs and Abstractions
The API layer of machine learning frameworks provides the primary interface through which developers interact with the framework’s capabilities. This layer must balance multiple competing demands: it must be intuitive enough for rapid development, flexible enough to support diverse use cases, and efficient enough to enable high-performance implementations.
Modern framework APIs typically implement multiple levels of abstraction. At the lowest level, they provide direct access to tensor operations and computational graph construction. These low-level APIs expose the fundamental operations discussed in the previous section, allowing fine-grained control over computation. For example, frameworks like PyTorch and TensorFlow offer such low-level interfaces, enabling researchers to define custom computations and explore novel algorithms (Ansel et al. 2024; Abadi et al. 2016).
# Low-level API example
import torch
# Manual tensor operations
x = torch.randn(2, 3)
w = torch.randn(3, 4)
b = torch.randn(4)
y = torch.matmul(x, w) + b
# Manual gradient computation
y.backward(torch.ones_like(y))Building on these primitives, frameworks implement higher-level APIs that package common patterns into reusable components. Neural network layers represent a classic example—while a convolution operation could be implemented manually using basic tensor operations, frameworks provide pre-built layer abstractions that handle the implementation details. This approach is exemplified by libraries such as PyTorch’s torch.nn and TensorFlow’s Keras API, which enable efficient and user-friendly model development (Chollet 2018).
# Mid-level API example using nn modules
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self):
super().__init__()
self.conv = nn.Conv2d(3, 64, kernel_size=3)
self.fc = nn.Linear(64, 10)
def forward(self, x):
x = self.conv(x)
x = torch.relu(x)
x = self.fc(x)
return xAt the highest level, frameworks often provide model-level abstractions that automate common workflows. For example, the Keras API provides a highly abstract interface that hides most implementation details:
# High-level API example using Keras
from tensorflow import keras
model = keras.Sequential([
keras.layers.Conv2D(64, 3, activation='relu', input_shape=(32, 32, 3)),
keras.layers.Flatten(),
keras.layers.Dense(10)
])
# Automated training workflow
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy')
model.fit(train_data, train_labels, epochs=10)The organization of these API layers reflects fundamental trade-offs in framework design. Lower-level APIs provide maximum flexibility but require more expertise to use effectively. Higher-level APIs improve developer productivity but may constrain implementation choices. Framework APIs must therefore provide clear paths between abstraction levels, allowing developers to mix different levels of abstraction as needed for their specific use cases.## Framework Components
Machine learning frameworks organize their fundamental capabilities into distinct components that work together to provide a complete development and deployment environment. These components create layers of abstraction that make frameworks both usable for high-level model development and efficient for low-level execution. Understanding how these components interact helps developers choose and use frameworks effectively.
7.4.2 Core Libraries
At the heart of every machine learning framework lies a set of core libraries, forming the foundation upon which all other components are built. These libraries provide the essential building blocks for machine learning operations, implementing fundamental tensor operations that serve as the backbone of numerical computations. Heavily optimized for performance, these operations often leverage low-level programming languages and hardware-specific optimizations to ensure efficient execution of tasks like matrix multiplication, a cornerstone of neural network computations.
Alongside these basic operations, core libraries implement automatic differentiation capabilities, enabling the efficient computation of gradients for complex functions. This feature is crucial for the backpropagation algorithm that powers most neural network training. The implementation often involves intricate graph manipulation and symbolic computation techniques, abstracting away the complexities of gradient calculation from the end-user.
Building upon these fundamental operations, core libraries typically provide pre-implemented neural network layers such as convolutional, recurrent, and attention mechanisms. These ready-to-use components save developers from reinventing the wheel for common model architectures, allowing them to focus on higher-level model design rather than low-level implementation details. Similarly, optimization algorithms like various flavors of gradient descent are provided out-of-the-box, further streamlining the model development process.
Here is a simplified example of how these components might be used in practice:
import torch
import torch.nn as nn
# Create a simple neural network
model = nn.Sequential(
nn.Linear(10, 20),
nn.ReLU(),
nn.Linear(20, 1)
)
# Define loss function and optimizer
loss_fn = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
# Forward pass, compute loss, and backward pass
x = torch.randn(32, 10)
y = torch.randn(32, 1)
y_pred = model(x)
loss = loss_fn(y_pred, y)
loss.backward()
optimizer.step()This example demonstrates how core libraries provide high-level abstractions for model creation, loss computation, and optimization, while handling low-level details internally.
7.4.3 Extensions and Plugins
While core libraries offer essential functionality, the true power of modern machine learning frameworks often lies in their extensibility. Extensions and plugins expand the capabilities of frameworks, allowing them to address specialized needs and leverage cutting-edge research. Domain-specific libraries, for instance, cater to particular areas like computer vision or natural language processing, providing pre-trained models, specialized data augmentation techniques, and task-specific layers.
Hardware acceleration plugins play an important role in performance optimization as it enables frameworks to take advantage of specialized hardware like GPUs or TPUs. These plugins dramatically speed up computations and allow seamless switching between different hardware backends, a key feature for scalability and flexibility in modern machine learning workflows.
As models and datasets grow in size and complexity, distributed computing extensions also become important. These tools enable training across multiple devices or machines, handling complex tasks like data parallelism, model parallelism, and synchronization between compute nodes. This capability is essential for researchers and companies tackling large-scale machine learning problems.
Complementing these computational tools are visualization and experiment tracking extensions. Visualization tools provide invaluable insights into the training process and model behavior, displaying real-time metrics and even offering interactive debugging capabilities. Experiment tracking extensions help manage the complexity of machine learning research, allowing systematic logging and comparison of different model configurations and hyperparameters.
7.4.4 Development Tools
The ecosystem of development tools surrounding a machine learning framework further enhances its effectiveness and adoption. Interactive development environments, such as Jupyter notebooks, have become nearly ubiquitous in machine learning workflows, allowing for rapid prototyping and seamless integration of code, documentation, and outputs. Many frameworks provide custom extensions for these environments to enhance the development experience.
Debugging and profiling tools address the unique challenges presented by machine learning models. Specialized debuggers allow developers to inspect the internal state of models during training and inference, while profiling tools identify bottlenecks in model execution, guiding optimization efforts. These tools are essential for developing efficient and reliable machine learning systems.
As projects grow in complexity, version control integration becomes increasingly important. Tools that allow versioning of not just code, but also model weights, hyperparameters, and training data, help manage the iterative nature of model development. This comprehensive versioning approach ensures reproducibility and facilitates collaboration in large-scale machine learning projects.
Finally, deployment utilities bridge the gap between development and production environments. These tools handle tasks like model compression, conversion to deployment-friendly formats, and integration with serving infrastructure, streamlining the process of moving models from experimental settings to real-world applications.
7.5 System Integration
System integration is about implementing machine learning frameworks in real-world environments. This section explores how ML frameworks integrate with broader software and hardware ecosystems, addressing the challenges and considerations at each level of the integration process.
7.5.1 Hardware Integration
Effective hardware integration is crucial for optimizing the performance of machine learning models. Modern ML frameworks must adapt to a diverse range of computing environments, from high-performance GPU clusters to resource-constrained edge devices.
For GPU acceleration, frameworks like TensorFlow and PyTorch provide robust support, allowing seamless utilization of NVIDIA’s CUDA platform. This integration enables significant speedups in both training and inference tasks. Similarly, support for Google’s TPUs in TensorFlow allows for even further acceleration of specific workloads.
In distributed computing scenarios, frameworks must efficiently manage multi-device and multi-node setups. This involves strategies for data parallelism, where the same model is replicated across devices, and model parallelism, where different parts of the model are distributed across hardware units. Frameworks like Horovod have emerged to simplify distributed training across different backend frameworks.
For edge deployment, frameworks are increasingly offering lightweight versions optimized for mobile and IoT devices. TensorFlow Lite and PyTorch Mobile, for instance, provide tools for model compression and optimization, ensuring efficient execution on devices with limited computational resources and power constraints.
7.5.2 Software Stack
Integrating ML frameworks into existing software stacks presents unique challenges and opportunities. A key consideration is how the ML system interfaces with data processing pipelines. Frameworks often provide connectors to popular big data tools like Apache Spark or Apache Beam, allowing seamless data flow between data processing systems and ML training environments.
Containerization technologies like Docker have become essential in ML workflows, ensuring consistency between development and production environments. Kubernetes has emerged as a popular choice for orchestrating containerized ML workloads, providing scalability and manageability for complex deployments.
ML frameworks must also interface with other enterprise systems such as databases, message queues, and web services. For instance, TensorFlow Serving provides a flexible, high-performance serving system for machine learning models, which can be easily integrated into existing microservices architectures.
7.5.3 Deployment Considerations
Deploying ML models to production environments involves several critical considerations. Model serving strategies must balance performance, scalability, and resource efficiency. Approaches range from batch prediction for large-scale offline processing to real-time serving for interactive applications.
Scaling ML systems to meet production demands often involves techniques like horizontal scaling of inference servers, caching of frequent predictions, and load balancing across multiple model versions. Frameworks like TensorFlow Serving and TorchServe provide built-in solutions for many of these scaling challenges.
Monitoring and logging are crucial for maintaining ML systems in production. This includes tracking model performance metrics, detecting concept drift, and logging prediction inputs and outputs for auditing purposes. Tools like Prometheus and Grafana are often integrated with ML serving systems to provide comprehensive monitoring solutions.
7.5.4 Workflow Orchestration
Managing end-to-end ML pipelines requires orchestrating multiple stages, from data preparation and model training to deployment and monitoring. MLOps practices have emerged to address these challenges, bringing DevOps principles to machine learning workflows.
Continuous Integration and Continuous Deployment (CI/CD) practices are being adapted for ML workflows. This involves automating model testing, validation, and deployment processes. Tools like Jenkins or GitLab CI can be extended with ML-specific stages to create robust CI/CD pipelines for machine learning projects.
Automated model retraining and updating is another critical aspect of ML workflow orchestration. This involves setting up systems to automatically retrain models on new data, evaluate their performance, and seamlessly update production models when certain criteria are met. Frameworks like Kubeflow provide end-to-end ML pipelines that can automate many of these processes.
Version control for ML assets, including data, model architectures, and hyperparameters, is essential for reproducibility and collaboration. Tools like DVC (Data Version Control) and MLflow have emerged to address these ML-specific version control needs.
7.6 Major Frameworks
As we have seen earlier, machine learning frameworks are complicated. Over the years, several machine learning frameworks have emerged, each with its unique strengths and ecosystem, but few have remained as industry standards. Here we examine the mature and major players in the field, starting with a comprehensive look at TensorFlow, followed by PyTorch, JAX, and other notable frameworks.
7.6.1 TF Ecosystem
TensorFlow was developed by the Google Brain team and was released as an open-source software library on November 9, 2015. It was designed for numerical computation using data flow graphs and has since become popular for a wide range of machine learning applications.
TensorFlow is a training and inference framework that provides built-in functionality to handle everything from model creation and training to deployment, as shown in Figure 7.10. Since its initial development, the TensorFlow ecosystem has grown to include many different “varieties” of TensorFlow, each intended to allow users to support ML on different platforms.
TensorFlow Core: primary package that most developers engage with. It provides a comprehensive, flexible platform for defining, training, and deploying machine learning models. It includes tf.keras as its high-level API.
TensorFlow Lite: designed for deploying lightweight models on mobile, embedded, and edge devices. It offers tools to convert TensorFlow models to a more compact format suitable for limited-resource devices and provides optimized pre-trained models for mobile.
TensorFlow Lite Micro: designed for running machine learning models on microcontrollers with minimal resources. It operates without the need for operating system support, standard C or C++ libraries, or dynamic memory allocation, using only a few kilobytes of memory.
TensorFlow.js: JavaScript library that allows training and deployment of machine learning models directly in the browser or on Node.js. It also provides tools for porting pre-trained TensorFlow models to the browser-friendly format.
TensorFlow on Edge Devices (Coral): platform of hardware components and software tools from Google that allows the execution of TensorFlow models on edge devices, leveraging Edge TPUs for acceleration.
TensorFlow Federated (TFF): framework for machine learning and other computations on decentralized data. TFF facilitates federated learning, allowing model training across many devices without centralizing the data.
TensorFlow Graphics: library for using TensorFlow to carry out graphics-related tasks, including 3D shapes and point clouds processing, using deep learning.
TensorFlow Hub: repository of reusable machine learning model components to allow developers to reuse pre-trained model components, facilitating transfer learning and model composition.
TensorFlow Serving: framework designed for serving and deploying machine learning models for inference in production environments. It provides tools for versioning and dynamically updating deployed models without service interruption.
TensorFlow Extended (TFX): end-to-end platform designed to deploy and manage machine learning pipelines in production settings. TFX encompasses data validation, preprocessing, model training, validation, and serving components.
7.6.2 PyTorch
PyTorch, developed by Facebook’s AI Research lab, has gained significant traction in the machine learning community, particularly among researchers and academics. Its design philosophy emphasizes ease of use, flexibility, and dynamic computation, which aligns well with the iterative nature of research and experimentation.
PyTorch’s architecture lies its dynamic computational graph system. Unlike the static graphs used in earlier versions of TensorFlow, PyTorch builds the computational graph on-the-fly during execution. This approach, often referred to as “define-by-run,” allows for more intuitive model design and easier debugging that we discussed earlier. Moreover, developers can use standard Python control flow statements within their models, and the graph structure can change from iteration to iteration. This flexibility is particularly advantageous when working with variable-length inputs or complex, dynamic neural network architectures.
PyTorch’s eager execution mode is tightly coupled with its dynamic graph approach. Operations are executed immediately as they are called, rather than being deferred for later execution in a static graph. This immediate execution facilitates easier debugging and allows for more natural integration with Python’s native debugging tools. The eager execution model aligns closely with PyTorch’s imperative programming style, which many developers find more intuitive and Pythonic.
PyTorch’s fundamental data structure is the tensor, similar to TensorFlow and other frameworks discussed in earlier sections. PyTorch tensors are conceptually equivalent to multi-dimensional arrays and can be manipulated using a rich set of operations. The framework provides seamless integration with CUDA, much like TensorFlow, enabling efficient GPU acceleration for tensor computations. PyTorch’s autograd system automatically tracks all operations performed on tensors, facilitating automatic differentiation for gradient-based optimization algorithms.
7.6.3 JAX
JAX, developed by Google Research, is a newer entrant in the field of machine learning frameworks. Unlike TensorFlow and PyTorch, which were primarily designed for deep learning, JAX focuses on high-performance numerical computing and advanced machine learning research. Its design philosophy centers around functional programming principles and composition of transformations, offering a fresh perspective on building and optimizing machine learning systems.
JAX is built as a NumPy-like library with added capabilities for automatic differentiation and just-in-time (JIT) compilation. This foundation makes JAX feel familiar to researchers accustomed to scientific computing in Python, while providing powerful tools for optimization and acceleration. Where TensorFlow uses static computational graphs and PyTorch employs dynamic ones, JAX takes a different approach altogether—a system for transforming numerical functions.
One of JAX’s key features is its powerful automatic differentiation system. Unlike TensorFlow’s static graph approach or PyTorch’s dynamic computation, JAX can differentiate native Python and NumPy functions, including those with loops, branches, and recursion. This capability extends beyond simple scalar-to-scalar functions, allowing for complex transformations like vectorization and JIT compilation. This flexibility is particularly valuable for researchers exploring novel machine learning techniques and architectures.
JAX leverages XLA (Accelerated Linear Algebra) for just-in-time compilation, similar to TensorFlow but with a more central role in its operation. This allows JAX to optimize and compile Python code for various hardware accelerators, including GPUs and TPUs. In contrast to PyTorch’s eager execution and TensorFlow’s graph optimization, JAX’s approach can lead to significant performance improvements, especially for complex computational patterns.
Where TensorFlow and PyTorch primarily use object-oriented and imperative programming models, JAX embraces functional programming. This approach encourages the use of pure functions and immutable data, which can lead to more predictable and easier-to-optimize code. It’s a significant departure from the stateful models common in other frameworks and can require a shift in thinking for developers accustomed to TensorFlow or PyTorch.
JAX introduces a set of composable function transformations that set it apart from both TensorFlow and PyTorch. These include automatic differentiation (grad), just-in-time compilation (jit), automatic vectorization (vmap), and parallel execution across multiple devices (pmap). These transformations can be composed, allowing for powerful and flexible operations that are not as straightforward in other frameworks.
7.6.4 Comparison
Table 7.3 provides a concise comparison of three major machine learning frameworks: TensorFlow, PyTorch, and JAX. These frameworks, while serving similar purposes, exhibit fundamental differences in their design philosophies and technical implementations.
| Aspect | TensorFlow | PyTorch | JAX |
|---|---|---|---|
| Graph Type | Static (1.x), Dynamic (2.x) | Dynamic | Functional transformations |
| Programming Model | Imperative (2.x), Symbolic (1.x) | Imperative | Functional |
| Core Data Structure | Tensor (mutable) | Tensor (mutable) | Array (immutable) |
| Execution Mode | Eager (2.x default), Graph | Eager | Just-in-time compilation |
| Automatic Differentiation | Reverse mode | Reverse mode | Forward and Reverse mode |
| Hardware Acceleration | CPU, GPU, TPU | CPU, GPU | CPU, GPU, TPU |
7.7 Framework Specialization
Machine learning frameworks have evolved significantly to meet the diverse needs of different computational environments. As ML applications expand beyond traditional data centers to encompass edge devices, mobile platforms, and even tiny microcontrollers, the need for specialized frameworks has become increasingly apparent.
Framework specialization refers to the process of tailoring ML frameworks to optimize performance, efficiency, and functionality for specific deployment environments. This specialization is crucial because the computational resources, power constraints, and use cases vary dramatically across different platforms.
The Open Neural Network Exchange (ONNX) format plays a vital role in framework interoperability across these specialized environments. ONNX provides a standardized representation for ML models, allowing them to move between different frameworks and deployment targets. This standardization helps bridge the gap between framework specializations, enabling models trained in one environment to be optimized and deployed in another.
Machine learning deployment environments shape how frameworks specialize and evolve. Cloud ML environments leverage high-performance servers that offer abundant computational resources for complex operations. Edge ML operates on devices with moderate computing power, where real-time processing often takes priority. Mobile ML adapts to the varying capabilities and energy constraints of smartphones and tablets. Tiny ML functions within the strict limitations of microcontrollers and other highly constrained devices that possess minimal resources.
Each of these environments presents unique challenges that influence framework design. Cloud frameworks prioritize scalability and distributed computing. Edge frameworks focus on low-latency inference and adaptability to diverse hardware. Mobile frameworks emphasize energy efficiency and integration with device-specific features. TinyML frameworks specialize in extreme resource optimization for severely constrained environments.
In the following sections, we will explore how ML frameworks adapt to each of these environments. We will examine the specific techniques and design choices that enable frameworks to address the unique challenges of each domain, highlighting the trade-offs and optimizations that characterize framework specialization.
7.7.1 Cloud ML Frameworks
Cloud ML frameworks are sophisticated software infrastructures designed to leverage the vast computational resources available in cloud environments. These frameworks specialize in three primary areas: distributed computing architectures, management of large-scale data and models, and integration with cloud-native services.
Distributed computing is a fundamental specialization of cloud ML frameworks. These frameworks implement advanced strategies for partitioning and coordinating computational tasks across multiple machines or graphics processing units (GPUs). This capability is essential for training large-scale models on massive datasets. Both TensorFlow and PyTorch, two leading cloud ML frameworks, offer robust support for distributed computing. TensorFlow’s graph-based approach (in its 1.x version) was particularly well-suited for distributed execution, while PyTorch’s dynamic computational graph allows for more flexible distributed training strategies.
The ability to handle large-scale data and models is another key specialization. Cloud ML frameworks are optimized to work with datasets and models that far exceed the capacity of single machines. This specialization is reflected in the data structures of these frameworks. For instance, both TensorFlow and PyTorch use mutable Tensor objects as their primary data structure, allowing for efficient in-place operations on large datasets. JAX, a more recent framework, uses immutable arrays, which can provide benefits in terms of functional programming paradigms and optimization opportunities in distributed settings.
Integration with cloud-native services is the third major specialization area. This integration enables automated resource scaling, seamless access to cloud storage, and incorporation of cloud-based monitoring and logging systems. The execution modes of different frameworks play a role here. TensorFlow 2.x and PyTorch both default to eager execution, which allows for easier integration with cloud services and debugging. JAX’s just-in-time compilation offers potential performance benefits in cloud environments by optimizing computations for specific hardware.
Hardware acceleration is an important aspect of cloud ML frameworks. All major frameworks support CPU and GPU execution, with TensorFlow and JAX also offering native support for Google’s TPU. NVIDIA’s TensorRT is an optimization tool dedicated for GPU-based inference, providing sophisticated optimizations like layer fusion, precision calibration13, and kernel auto-tuning to maximize throughput on NVIDIA GPUs. These hardware acceleration options allow cloud ML frameworks to efficiently utilize the diverse computational resources available in cloud environments.
13 A process of adjusting computations to use reduced numerical precision, balancing performance improvements with acceptable losses in accuracy.
The automatic differentiation capabilities of these frameworks are particularly important in cloud settings where complex models with millions of parameters are common. While TensorFlow and PyTorch primarily use reverse-mode differentiation, JAX’s support for both forward and reverse-mode differentiation can offer advantages in certain large-scale optimization scenarios.
These specializations enable cloud ML frameworks to fully utilize the scalability and computational power of cloud infrastructure. However, this capability comes with increased complexity in deployment and management, often requiring specialized knowledge to fully leverage these frameworks. The focus on scalability and integration makes cloud ML frameworks particularly suitable for large-scale research projects, enterprise-level ML applications, and scenarios requiring massive computational resources.
7.7.2 Edge ML Frameworks
Edge ML frameworks are specialized software tools designed to facilitate machine learning operations in edge computing environments, characterized by proximity to data sources, stringent latency requirements, and limited computational resources. Examples of popular edge ML frameworks include TensorFlow Lite and Edge Impulse. The specialization of these frameworks addresses three primary challenges: real-time inference optimization, adaptation to heterogeneous hardware, and resource-constrained operation.
Real-time inference optimization is a critical feature of edge ML frameworks. This often involves leveraging different execution modes and graph types. For instance, while TensorFlow Lite (the edge-focused version of TensorFlow) uses a static graph approach to optimize inference, frameworks like PyTorch Mobile maintain a dynamic graph capability, allowing for more flexible model structures at the cost of some performance. The choice between static and dynamic graphs in edge frameworks often is a trade-off between optimization potential and model flexibility.
Adaptation to heterogeneous hardware is crucial for edge deployments. Edge ML frameworks extend the hardware acceleration capabilities of their cloud counterparts but with a focus on edge-specific hardware. For instance, TensorFlow Lite supports acceleration on mobile GPUs and edge TPUs, while frameworks like ARM’s Compute Library optimize for ARM-based processors. This specialization often involves custom operator implementations and low-level optimizations specific to edge hardware.
Operating within resource constraints is another aspect of edge ML framework specialization. This is reflected in the data structures and execution models of these frameworks. For instance, many edge frameworks use quantized tensors as their primary data structure, representing values with reduced precision (e.g., 8-bit integers instead of 32-bit floats) to decrease memory usage and computational demands. The automatic differentiation capabilities, while crucial for training in cloud environments, are often stripped down or removed entirely in edge frameworks to reduce model size and improve inference speed.
Edge ML frameworks also often include features for model versioning and updates, allowing for the deployment of new models with minimal system downtime. Some frameworks support limited on-device learning, enabling models to adapt to local data without compromising data privacy.
The specializations of edge ML frameworks collectively enable high-performance inference in resource-constrained environments. This capability expands the potential applications of AI in areas with limited cloud connectivity or where real-time processing is crucial. However, effective utilization of these frameworks requires careful consideration of target hardware specifications and application-specific requirements, necessitating a balance between model accuracy and resource utilization.
7.7.3 Mobile ML Frameworks
Mobile ML frameworks are specialized software tools designed for deploying and executing machine learning models on smartphones and tablets. Examples include TensorFlow Lite and Apple’s Core ML. These frameworks address the unique challenges of mobile environments, including limited computational resources, constrained power consumption, and diverse hardware configurations. The specialization of mobile ML frameworks primarily focuses on on-device inference optimization, energy efficiency, and integration with mobile-specific hardware and sensors.
On-device inference optimization in mobile ML frameworks often involves a careful balance between graph types and execution modes. For instance, TensorFlow Lite, also a popular mobile ML framework, uses a static graph approach to optimize inference performance. This contrasts with the dynamic graph capability of PyTorch Mobile, which offers more flexibility at the cost of some performance. The choice between static and dynamic graphs in mobile frameworks is a trade-off between optimization potential and model adaptability, crucial in the diverse and changing mobile environment.
The data structures in mobile ML frameworks are optimized for efficient memory usage and computation. While cloud-based frameworks like TensorFlow and PyTorch use mutable tensors, mobile frameworks often employ more specialized data structures. For example, many mobile frameworks use quantized tensors, representing values with reduced precision (e.g., 8-bit integers instead of 32-bit floats) to decrease memory footprint and computational demands. This specialization is critical given the limited RAM and processing power of mobile devices.
Energy efficiency, a paramount concern in mobile environments, influences the design of execution modes in mobile ML frameworks. Unlike cloud frameworks that may use eager execution for ease of development, mobile frameworks often prioritize graph-based execution for its potential energy savings. For instance, Apple’s Core ML uses a compiled model approach, converting ML models into a form that can be efficiently executed by iOS devices, optimizing for both performance and energy consumption.
Integration with mobile-specific hardware and sensors is another key specialization area. Mobile ML frameworks extend the hardware acceleration capabilities of their cloud counterparts but with a focus on mobile-specific processors. For example, TensorFlow Lite can leverage mobile GPUs and neural processing units (NPUs) found in many modern smartphones. Qualcomm’s Neural Processing SDK is designed to efficiently utilize the AI accelerators present in Snapdragon SoCs. This hardware-specific optimization often involves custom operator implementations and low-level optimizations tailored for mobile processors.
Automatic differentiation, while crucial for training in cloud environments, is often minimized or removed entirely in mobile frameworks to reduce model size and improve inference speed. Instead, mobile ML frameworks focus on efficient inference, with model updates typically performed off-device and then deployed to the mobile application.
Mobile ML frameworks also often include features for model updating and versioning, allowing for the deployment of improved models without requiring full app updates. Some frameworks support limited on-device learning, enabling models to adapt to user behavior or environmental changes without compromising data privacy.
The specializations of mobile ML frameworks collectively enable the deployment of sophisticated ML models on resource-constrained mobile devices. This expands the potential applications of AI in mobile environments, ranging from real-time image and speech recognition to personalized user experiences. However, effectively utilizing these frameworks requires careful consideration of the target device capabilities, user experience requirements, and privacy implications, necessitating a balance between model performance and resource utilization.
7.7.4 TinyML Frameworks
TinyML frameworks are specialized software infrastructures designed for deploying machine learning models on extremely resource-constrained devices, typically microcontrollers and low-power embedded systems. These frameworks address the severe limitations in processing power, memory, and energy consumption characteristic of tiny devices. The specialization of TinyML frameworks primarily focuses on extreme model compression, optimizations for severely constrained environments, and integration with microcontroller-specific architectures.
Extreme model compression in TinyML frameworks takes the quantization techniques mentioned in mobile and edge frameworks to their logical conclusion. While mobile frameworks might use 8-bit quantization, TinyML often employs even more aggressive techniques, such as 4-bit, 2-bit, or even 1-bit (binary) representations of model parameters. Frameworks like TensorFlow Lite Micro exemplify this approach (David et al. 2021), pushing the boundaries of model compression to fit within the kilobytes of memory available on microcontrollers.
The execution model in TinyML frameworks is highly specialized. Unlike the dynamic graph capabilities seen in some cloud and mobile frameworks, TinyML frameworks almost exclusively use static, highly optimized graphs. The just-in-time compilation approach seen in frameworks like JAX is typically not feasible in TinyML due to memory constraints. Instead, these frameworks often employ ahead-of-time compilation techniques to generate highly optimized, device-specific code.
Memory management in TinyML frameworks is far more constrained than in other environments. While edge and mobile frameworks might use dynamic memory allocation, TinyML frameworks like uTensor often rely on static memory allocation to avoid runtime overhead and fragmentation. This approach requires careful planning of the memory layout at compile time, a stark contrast to the more flexible memory management in cloud-based frameworks.
Hardware integration in TinyML frameworks is highly specific to microcontroller architectures. Unlike the general GPU support seen in cloud frameworks or the mobile GPU/NPU support in mobile frameworks, TinyML frameworks often provide optimizations for specific microcontroller instruction sets. For example, ARM’s CMSIS-NN (Lai, Suda, and Chandra 2018) provides optimized neural network kernels for Cortex-M series microcontrollers, which are often integrated into TinyML frameworks.
The concept of automatic differentiation, central to cloud-based frameworks and present to some degree in edge and mobile frameworks, is typically absent in TinyML frameworks. The focus is almost entirely on inference, with any learning or model updates usually performed off-device due to the severe computational constraints.
TinyML frameworks also specialize in power management to a degree not seen in other ML environments. Features like duty cycling and ultra-low-power wake-up capabilities are often integrated directly into the ML pipeline, enabling always-on sensing applications that can run for years on small batteries.
The extreme specialization of TinyML frameworks enables ML deployments in previously infeasible environments, from smart dust sensors to implantable medical devices. However, this specialization comes with significant trade-offs in model complexity and accuracy, requiring careful consideration of the balance between ML capabilities and the severe resource constraints of target devices.
7.8 Choosing a Framework
Framework selection builds on our understanding of framework specialization across computing environments. Engineers must evaluate three interdependent factors when choosing a framework: model requirements, hardware constraints, and software dependencies. The TensorFlow ecosystem demonstrates how these factors shape framework design through its variants: TensorFlow, TensorFlow Lite, and TensorFlow Lite Micro.
Figure 7.11 illustrates key differences between TensorFlow variants. Each variant represents specific trade-offs between computational capability and resource requirements. These trade-offs manifest in supported operations, binary size, and integration requirements.
Engineers analyze three primary aspects when selecting a framework:
- Model requirements determine which operations and architectures the framework must support
- Software dependencies define operating system and runtime requirements
- Hardware constraints establish memory and processing limitations
This systematic analysis enables engineers to select frameworks that align with their deployment requirements. As we examine the TensorFlow variants, we will explore how each aspect influences framework selection and shapes the capabilities of deployed machine learning systems.
7.8.1 Model Requirements
Model architecture capabilities vary significantly across TensorFlow variants, with clear trade-offs between functionality and efficiency. Figure 7.11 quantifies these differences across four key dimensions: training capability, inference efficiency, operation support, and quantization features.
TensorFlow supports approximately 1,400 operations and enables both training and inference. However, as Figure 7.11 indicates, its inference capabilities are inefficient for edge deployment. TensorFlow Lite reduces the operation count to roughly 130 operations while improving inference efficiency. It eliminates training support but adds native quantization tooling. TensorFlow Lite Micro further constrains the operation set to approximately 50 operations, achieving even higher inference efficiency through these constraints. Like TensorFlow Lite, it includes native quantization support but removes training capabilities.
This progressive reduction in operations enables deployment on increasingly constrained devices. The addition of native quantization in both TensorFlow Lite and TensorFlow Lite Micro provides essential optimization capabilities absent in the full TensorFlow framework. Quantization transforms models to use lower precision operations, reducing computational and memory requirements for resource-constrained deployments.
7.8.2 Software Dependencies
Figure 7.12 reveals three key software considerations that differentiate TensorFlow variants: operating system requirements, memory management capabilities, and accelerator support. These differences reflect each variant’s optimization for specific deployment environments.
Operating system dependencies mark a fundamental distinction between variants. TensorFlow and TensorFlow Lite require an operating system, while TensorFlow Lite Micro operates without OS support. This enables TensorFlow Lite Micro to reduce memory overhead and startup time, though it can still integrate with real-time operating systems like FreeRTOS, Zephyr, and Mbed OS when needed.
Memory management capabilities also distinguish the variants. TensorFlow Lite and TensorFlow Lite Micro support model memory mapping, enabling direct model access from flash storage rather than loading into RAM. TensorFlow lacks this capability, reflecting its design for environments with abundant memory resources. Memory mapping becomes increasingly important as deployment moves toward resource-constrained devices.
Accelerator delegation capabilities further differentiate the variants. Both TensorFlow and TensorFlow Lite support delegation to accelerators, enabling efficient computation distribution. TensorFlow Lite Micro omits this feature, acknowledging the limited availability of specialized accelerators in embedded systems. This design choice maintains the framework’s minimal footprint while matching typical embedded hardware configurations.
7.8.3 Hardware Constraints
Figure 7.13 quantifies the hardware requirements across TensorFlow variants through three metrics: base binary size, memory footprint, and processor architecture support. These metrics demonstrate the progressive optimization for constrained computing environments.
Binary size requirements decrease significantly across variants. TensorFlow requires over 3MB for its base binary, reflecting its comprehensive feature set. TensorFlow Lite reduces this to 100KB by eliminating training capabilities and unused operations. TensorFlow Lite Micro achieves a remarkable 10KB binary size through aggressive optimization and feature reduction.
Memory footprint follows a similar pattern of reduction. TensorFlow requires approximately 5MB of base memory, while TensorFlow Lite operates within 300KB. TensorFlow Lite Micro further reduces memory requirements to 20KB, enabling deployment on highly constrained devices.
Processor architecture support aligns with each variant’s intended deployment environment. TensorFlow supports x86 processors and accelerators including TPUs and GPUs, enabling high-performance computing in data centers. TensorFlow Lite targets mobile and edge processors, supporting Arm Cortex-A and x86 architectures. TensorFlow Lite Micro specializes in microcontroller deployment, supporting Arm Cortex-M cores, digital signal processors (DSPs), and various microcontroller units (MCUs) including STM32, NXP Kinetis, and Microchip AVR.
7.8.4 Additional Selection Factors
Framework selection for embedded systems extends beyond technical specifications of model architecture, hardware requirements, and software dependencies. Additional factors affect development efficiency, maintenance requirements, and deployment success. These factors require systematic evaluation to ensure optimal framework selection.
Performance Optimization
Performance in embedded systems encompasses multiple metrics beyond computational speed. Framework evaluation must consider:
Inference latency determines system responsiveness and real-time processing capabilities. Memory utilization affects both static storage requirements and runtime efficiency. Power consumption impacts battery life and thermal management requirements. Frameworks must provide optimization tools for these metrics, including quantization, operator fusion, and hardware-specific acceleration.
Deployment Scalability
Scalability requirements span both technical capabilities and operational considerations. Framework support must extend across deployment scales and scenarios:
Device scaling enables consistent deployment from microcontrollers to more powerful embedded processors. Operational scaling supports the transition from development prototypes to production deployments. Version management facilitates model updates and maintenance across deployed devices. The framework must maintain consistent performance characteristics throughout these scaling dimensions.
7.9 Conclusion
AI frameworks have evolved from basic numerical libraries into sophisticated software systems that shape how we develop and deploy machine learning applications. The progression from early numerical computing to modern deep learning frameworks demonstrates the field’s rapid technological advancement.
Modern frameworks like TensorFlow, PyTorch, and JAX implement distinct approaches to common challenges in machine learning development. Each framework offers varying tradeoffs between ease of use, performance, and flexibility. TensorFlow emphasizes production deployment, PyTorch focuses on research and experimentation, while JAX prioritizes functional programming patterns.
The specialization of frameworks into cloud, edge, mobile, and tiny ML implementations reflects the diverse requirements of machine learning applications. Cloud frameworks optimize for scalability and distributed computing. Edge and mobile frameworks prioritize model efficiency and reduced resource consumption. TinyML frameworks target constrained environments with minimal computing resources.
Understanding framework architecture, from tensor operations to execution models, enables developers to select appropriate tools for specific use cases, optimize application performance, debug complex computational graphs, and deploy models across different computing environments.
The continuing evolution of AI frameworks will likely focus on improving developer productivity, hardware acceleration, and deployment flexibility. These advancements will shape how machine learning systems are built and deployed across increasingly diverse computing environments.