10 Model Optimizations

DALL·E 3 Prompt: Illustration of a neural network model represented as a busy construction site, with a diverse group of construction workers, both male and female, of various ethnicities, labeled as ‘pruning’, ‘quantization’, and ‘sparsity’. They are working together to make the neural network more efficient and smaller, while maintaining high accuracy. The ‘pruning’ worker, a Hispanic female, is cutting unnecessary connections from the middle of the network. The ‘quantization’ worker, a Caucasian male, is adjusting or tweaking the weights all over the place. The ‘sparsity’ worker, an African female, is removing unnecessary nodes to shrink the model. Construction trucks and cranes are in the background, assisting the workers in their tasks. The neural network is visually transforming from a complex and large structure to a more streamlined and smaller one.

Purpose

How do neural network models transition from design to practical deployment, and what challenges arise in making them efficient and scalable?

Developing machine learning models goes beyond achieving high accuracy; real-world deployment introduces constraints that demand careful adaptation. Models must operate within the limits of computation, memory, latency, and energy efficiency, all while maintaining effectiveness. As models grow in complexity and scale, ensuring their feasibility across diverse hardware and applications becomes increasingly challenging. This necessitates a deeper understanding of the fundamental trade-offs between accuracy and efficiency, as well as the strategies that enable models to function optimally in different environments. By addressing these challenges, we establish guiding principles for transforming machine learning advancements into practical, scalable systems.

Learning Objectives

Identify, compare, and contrast various techniques for optimizing model representation.
Assess the trade-offs between different precision reduction strategies.
Evaluate how hardware-aware model design influences computation and memory efficiency.
Explain the role of dynamic computation techniques in improving efficiency.
Analyze the benefits and challenges of sparsity in model optimization and its hardware implications.
Discuss how different optimization strategies interact and impact system-level performance.

10.1 Overview

As machine learning models evolve in complexity and become increasingly ubiquitous, the focus shifts from solely enhancing accuracy to ensuring that models are practical, scalable, and efficient. The substantial computational requirements for training and deploying state-of-the-art models frequently surpass the limitations imposed by real-world environments, whether in expansive data centers or on resource-constrained mobile devices. Additionally, considerations such as memory constraints, energy consumption, and inference latency critically influence the effective deployment of these models. Model optimization, therefore, serves as the framework that reconciles advanced modeling techniques with practical system limitations, ensuring that enhanced performance is achieved without compromising operational viability.

Definition of Model Optimization

Model Optimization is the systematic refinement of machine learning models to enhance their efficiency while maintaining effectiveness. This process involves balancing trade-offs between accuracy, computational cost, memory usage, latency, and energy efficiency to ensure models can operate within real-world constraints. Model optimization is driven by fundamental principles such as reducing redundancy, improving numerical representation, and structuring computations more efficiently. These principles guide the adaptation of models across diverse deployment environments, from cloud-scale infrastructure to resource-constrained edge devices, enabling scalable, practical, and high-performance machine learning systems.

The necessity for model optimization arises from the inherent limitations of modern computational systems. Machine learning models function within a multifaceted ecosystem encompassing hardware capabilities, software frameworks, and diverse deployment scenarios. A model that excels in controlled research environments may prove unsuitable for practical applications due to prohibitive computational costs or substantial memory requirements. Consequently, optimization techniques are critical for aligning high-performing models with the practical constraints of real-world systems.

Optimization is inherently context-dependent. Models deployed in cloud environments often prioritize scalability and throughput, whereas those intended for edge devices must emphasize low power consumption and minimal memory footprint. The array of optimization strategies available enables the adjustment of models to accommodate these divergent constraints without compromising their predictive accuracy.

This chapter explores the principles of model optimization from a systems perspective. Figure Figure 10.1 illustrates the three distinct layers of the optimization stack discussed in the chapter. At the highest level, methodologies aimed at reducing model parameter complexity while preserving inferential capabilities are introduced. Techniques such as pruning and knowledge distillation are examined for their ability to compress and refine models, thereby enhancing model quality and improving system runtime performance.

Figure 10.1: Three layers to be covered.

We also investigate the role of numerical precision in model computations. An understanding of how various numerical representations affect model size, speed, and accuracy is essential for achieving optimal performance. Accordingly, the trade-offs associated with different numerical formats and the implementation of reduced-precision arithmetic are discussed, a topic of particular importance for embedded system deployments where computational resources are constrained.

At the lowest layer, the intricacies of hardware-software co-design are examined, which elucidates how models can be systematically tailored to efficiently utilize the specific characteristics of target hardware platforms. Alignment of machine learning model design with hardware architecture may yield substantial gains in performance and efficiency.

On the whole, the chapter systematically examines the underlying factors that shape optimization approaches, including model representation, numerical precision, and architectural efficiency. In addition, the interdependencies between software and hardware are explored, with emphasis on the roles played by compilers, runtimes, and specialized accelerators in influencing optimization choices. A structured framework is ultimately proposed to guide the selection and application of optimization techniques, ensuring that machine learning models remain both effective and viable under real-world conditions.

10.2 Models in the Real World

Machine learning models are rarely deployed in isolation—they operate as part of larger systems with complex constraints, dependencies, and trade-offs. Model optimization, therefore, cannot be treated as a purely algorithmic problem; it must be viewed as a systems-level challenge that considers computational efficiency, scalability, deployment feasibility, and overall system performance. A well-optimized model must balance multiple objectives, including inference speed, memory footprint, power consumption, and accuracy, all while aligning with the specific requirements of the target deployment environment.

Therefore, it is important to understand the systems perspective on model optimization, highlighting why optimization is essential, the key constraints that drive optimization efforts, and the principles that define an effective optimization strategy. By framing optimization as a systems problem, we can move beyond ad-hoc techniques and instead develop principled approaches that integrate hardware, software, and algorithmic considerations into a unified optimization framework.

10.2.1 Making Models Practical

Modern machine learning models often achieve impressive accuracy on benchmark datasets, but making them practical for real-world use is far from trivial. In practice, machine learning systems operate under a range of computational, memory, latency, and energy constraints that significantly impact both training and inference (Choudhary et al. 2020). A model that performs well in a research setting may be impractical when integrated into a broader system, whether it is deployed in the cloud, embedded in a smartphone, or running on a tiny microcontroller.

Choudhary, Tejalal, Vipul Mishra, Anurag Goswami, and Jagannathan Sarangapani. 2020. “A Comprehensive Survey on Model Compression and Acceleration.” Artificial Intelligence Review 53: 5113–55. https://doi.org/10.1007/s10462-020-09816-7.

Dean, Jeffrey, David Patterson, and Cliff Young. 2018. “A New Golden Age in Computer Architecture: Empowering the Machine-Learning Revolution.” IEEE Micro 38 (2): 21–29.

Banbury, Colby R., Vijay Janapa Reddi, Max Lam, William Fu, Amin Fazel, Jeremy Holleman, Xinyuan Huang, et al. 2020. “Benchmarking TinyML Systems: Challenges and Direction.” arXiv Preprint arXiv:2003.04821. https://arxiv.org/abs/2003.04821.

The real-world feasibility of a model depends on more than just accuracy—it also hinges on how efficiently it can be trained, stored, and executed. In large-scale Cloud ML settings, optimizing models helps minimize training time, computational cost, and power consumption, making large-scale AI workloads more efficient (Dean, Patterson, and Young 2018). In contrast, Edge ML requires models to run with limited compute resources, necessitating optimizations that reduce memory footprint and computational complexity. Mobile ML introduces additional constraints, such as battery life and real-time responsiveness, while Tiny ML pushes efficiency to the extreme, requiring models to fit within the memory and processing limits of ultra-low-power devices (Banbury et al. 2020).

Optimization also plays a crucial role in making AI more sustainable and accessible. Reducing a model’s energy footprint is critical as AI workloads scale, helping mitigate the environmental impact of large-scale ML training and inference (Patterson et al. 2021). At the same time, optimized models can expand the reach of machine learning, enabling applications in low-resource environments, from rural healthcare to autonomous systems operating in the field.

Patterson, David, Joseph Gonzalez, Quoc Le, Chen Liang, Lluis-Miquel Munguia, Daniel Rothchild, David So, Maud Texier, and Jeff Dean. 2021. “Carbon Emissions and Large Neural Network Training.” arXiv Preprint arXiv:2104.10350.

Ultimately, without systematic optimization, many machine learning models remain confined to academic studies rather than progressing to practical applications. For ML systems engineers and practitioners, the primary objective is to bridge the gap between theoretical potential and real-world functionality by deliberately designing models that are both efficient in execution and robust in diverse operational environments.

10.2.2 Balancing Accuracy and Efficiency

Machine learning models are typically optimized to achieve high accuracy, but improving accuracy often comes at the cost of increased computational complexity. Larger models with more parameters, deeper architectures, and higher numerical precision can yield better performance on benchmark tasks. However, these improvements introduce challenges related to memory footprint, inference latency, power consumption, and training efficiency. As machine learning systems are deployed across a wide range of hardware platforms, balancing accuracy and efficiency becomes a fundamental challenge in model optimization.

From a systems perspective, accuracy and efficiency are often in direct tension. Increasing model capacity—whether through more parameters, deeper layers, or larger input resolutions—generally enhances predictive performance. However, these same modifications also increase computational cost, making inference slower and more resource-intensive. Similarly, during training, larger models demand greater memory bandwidth, longer training times, and more energy consumption, all of which introduce scalability concerns.

The need for efficiency constraints extends beyond inference. Training efficiency is critical for both research and industrial-scale applications, as larger models require greater computational resources and longer convergence times. Unoptimized training pipelines can result in prohibitive costs and delays, limiting the pace of innovation and deployment. On the inference side, real-time applications impose strict constraints on latency and power consumption, further motivating the need for optimization.

Balancing accuracy and efficiency requires a structured approach to model optimization, where trade-offs are carefully analyzed rather than applied indiscriminately. Some optimizations, such as pruning redundant parameters or reducing numerical precision, can improve efficiency without significantly impacting accuracy. Other techniques, like model distillation or architecture search, aim to preserve predictive performance while improving computational efficiency. The key challenge is to systematically determine which optimizations provide the best trade-offs for a given application and hardware platform.

10.2.3 System Constraints Driving Optimization

Machine learning models operate within a set of fundamental system constraints that influence how they are designed, trained, and deployed. These constraints arise from the computational resources available, the hardware on which the model runs, and the operational requirements of the application. Understanding these constraints is essential for developing effective optimization strategies that balance accuracy, efficiency, and feasibility. The primary system constraints that drive model optimization include:

Computational Cost: Training and inference require significant compute resources, especially for large-scale models. The computational complexity of a model affects the feasibility of training on large datasets and deploying real-time inference workloads. Optimization techniques that reduce computation—such as pruning, quantization, or efficient architectures—can significantly lower costs.

Memory and Storage Limitations: Models must fit within the memory constraints of the target system. This includes RAM limitations during execution and storage constraints for model persistence. Large models with billions of parameters may exceed the capacity of edge devices or embedded systems, necessitating optimizations that reduce memory footprint without compromising performance.

Latency and Throughput: Many applications impose real-time constraints, requiring models to produce predictions within strict latency budgets. In autonomous systems, healthcare diagnostics, and interactive AI applications, slow inference times can render a model unusable. Optimizing model execution—through reduced precision arithmetic, efficient data movement, or parallel computation—can help meet real-time constraints.

Energy Efficiency and Power Consumption: Power constraints are critical in mobile, edge, and embedded AI systems. High energy consumption impacts battery-powered devices and increases operational costs in large-scale cloud deployments. Techniques such as model sparsity, adaptive computation, and hardware-aware optimization contribute to energy-efficient AI.

Scalability and Hardware Compatibility: Model optimizations must align with the capabilities of the target hardware. A model optimized for specialized accelerators (e.g., GPUs, TPUs, FPGAs) may not perform efficiently on general-purpose CPUs. Additionally, scaling models across distributed systems introduces new challenges in synchronization and workload balancing.

These constraints are interdependent, meaning that optimizing for one factor may impact another. For example, reducing numerical precision can lower memory usage and improve inference speed but may introduce quantization errors that degrade accuracy. Similarly, aggressive pruning can reduce computation but may lead to diminished generalization if not carefully managed.

10.3 Three Core Dimensions of Model Optimization

Machine learning models must balance accuracy, efficiency, and feasibility to operate effectively in real-world systems. As discussed in the previous section, optimization is necessary to address key system constraints such as computational cost, memory limitations, energy efficiency, and latency requirements. However, model optimization is not a single technique but a structured process that can be categorized into three fundamental dimensions: model representation optimization, numerical precision optimization, and architectural efficiency optimization.

Each of these dimensions addresses a distinct aspect of efficiency. Model representation optimization focuses on modifying the architecture of the model itself to reduce redundancy while preserving accuracy. Numerical precision optimization improves efficiency by adjusting how numerical values are stored and computed, reducing the computational and memory overhead of machine learning operations. Architectural efficiency focuses on optimizing how computations are executed, ensuring that operations are performed efficiently across different hardware platforms.

Understanding these three dimensions provides a structured framework for systematically improving model efficiency. Rather than applying ad hoc techniques, machine learning practitioners must carefully select optimizations based on their impact across these dimensions, considering trade-offs between accuracy, efficiency, and deployment constraints.

10.3.1 Model Representation

The first dimension, model representation optimization, focuses on reducing redundancy in the structure of machine learning models. Large models often contain excessive parameters that contribute little to overall performance but significantly increase memory footprint and computational cost. Optimizing model representation involves techniques that remove unnecessary components while maintaining predictive accuracy. Common approaches include pruning, which eliminates redundant weights and neurons, and knowledge distillation, where a smaller model learns to approximate the behavior of a larger model. Additionally, automated architecture search methods refine model structures to balance efficiency and accuracy. These optimizations primarily impact how models are designed at an algorithmic level, ensuring that they remain effective while being computationally manageable.

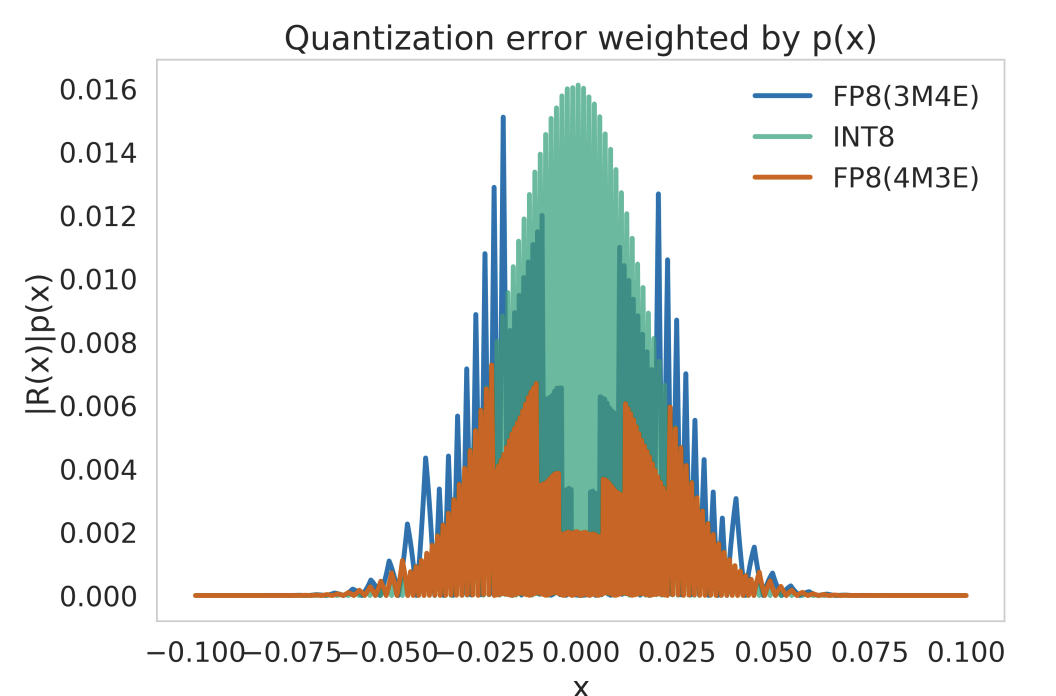
10.3.2 Numerical Precision

The second dimension, numerical precision optimization, addresses how numerical values are represented and processed within machine learning models. Reducing the precision of computations can significantly lower the memory and computational requirements of a model, particularly for machine learning workloads. Quantization techniques map high-precision weights and activations to lower-bit representations, enabling efficient execution on hardware accelerators such as GPUs, TPUs, and specialized AI chips. Mixed-precision training dynamically adjusts precision levels during training to strike a balance between efficiency and accuracy. By carefully optimizing numerical precision, models can achieve substantial reductions in computational cost while maintaining acceptable levels of accuracy.

10.3.3 Architectural Efficiency

The third dimension, architectural efficiency, focuses on how computations are performed efficiently during both training and inference. A well-designed model structure is not sufficient if its execution is suboptimal. Many machine learning models contain redundancies in their computational graphs, leading to inefficiencies in how operations are scheduled and executed. Architectural efficiency involves techniques that exploit sparsity in both model weights and activations, factorize large computational components into more efficient forms, and dynamically adjust computation based on input complexity. These methods improve execution efficiency across different hardware platforms, reducing latency and power consumption. In addition to inference optimizations, architectural efficiency also applies to training, where techniques such as gradient checkpointing and low-rank adaptation help reduce memory overhead and computational demands.

10.3.4 The Tripartite Framework

These three dimensions collectively provide a framework for understanding model optimization. While each category targets different aspects of efficiency, they are highly interconnected. Pruning, for example, primarily falls under model representation but also affects architectural efficiency by reducing the number of operations performed during inference. Quantization reduces numerical precision but can also impact memory footprint and execution efficiency. Understanding these interdependencies is crucial for selecting the right combination of optimizations for a given system.

The choice of optimizations is driven by system constraints, which define the practical limitations within which models must operate. A machine learning model deployed in a data center has different constraints from one running on a mobile device or an embedded system. Computational cost, memory usage, inference latency, and energy efficiency all influence which optimizations are most appropriate for a given scenario. A model that is too large for a resource-constrained device may require aggressive pruning and quantization, while a latency-sensitive application may benefit from operator fusion and hardware-aware scheduling.

Table Table 10.1 summarizes how different system constraints map to the three core dimensions of model optimization.

Table 10.1: Mapping of system constraints to optimization dimensions.

System Constraint	Model Representation	Numerical Precision	Architectural Efficiency
Computational Cost	✗	✓	✓
Memory and Storage	✓	✓	✗
Latency and Throughput	✓	✗	✓
Energy Efficiency	✗	✓	✓
Scalability	✓	✗	✓

This mapping highlights the interdependence between optimization strategies and real-world constraints. Although each system constraint primarily aligns with one or more optimization dimensions, the relationships are not strictly one-to-one. Many optimization techniques affect multiple constraints simultaneously. Structuring model optimization along these three dimensions and mapping techniques to specific system constraints enables practitioners to analyze trade-offs more effectively and select optimizations that best align with deployment requirements. The following sections explore each optimization dimension in detail, highlighting the key techniques and their impact on model efficiency.

10.4 Optimizing Model Representation

Model representation plays a key role in determining the computational and memory efficiency of a machine learning system. The way a model is structured, not just in terms of the number of parameters but also how these parameters interact, directly affects its ability to scale, deploy efficiently, and generalize effectively. Optimizing model representation involves reducing redundancy, restructuring architectures for efficiency, and leveraging automated design methods to find optimal configurations.

The primary goal of model representation optimization is to eliminate unnecessary complexity while preserving model performance. Many state-of-the-art models are designed to maximize accuracy with little regard for efficiency, leading to architectures with excessive parameters, redundant computations, and inefficient data flow. In real-world deployment scenarios, these inefficiencies translate into higher computational costs, increased memory usage, and slower inference times. Addressing these issues requires systematically restructuring the model to remove redundancy, minimize unnecessary computations, and ensure that every parameter contributes meaningfully to the task at hand.

From a systems perspective, model representation optimization focuses on two key objectives. First, reducing redundancy by eliminating unnecessary parameters, neurons, or layers while preserving model accuracy. Many models are overparameterized, meaning that a smaller version could achieve similar performance with significantly lower computational overhead. Second, structuring computations efficiently to ensure that the model’s architecture aligns well with modern hardware capabilities, such as leveraging parallel processing and minimizing costly memory operations. An unoptimized model may be unnecessarily large, leading to slower inference times, higher energy consumption, and increased deployment costs. Conversely, an overly compressed model may lose too much predictive accuracy, making it unreliable for real-world use. The challenge in model representation optimization is to strike a balance between model size, accuracy, and efficiency, selecting techniques that reduce computational complexity while maintaining strong generalization.

To systematically approach model representation optimization, we focus on three key techniques that have proven effective in balancing efficiency and accuracy. Pruning systematically removes parameters or entire structural components that contribute little to overall performance, reducing computational and memory overhead while preserving accuracy. Knowledge distillation transfers knowledge from a large, high-capacity model to a smaller, more efficient model, enabling smaller models to retain predictive power while reducing computational cost. Finally, NAS automates the process of designing models optimized for specific constraints, leveraging machine learning itself to explore and refine model architectures.

We focus on these three techniques because they represent distinct but complementary approaches to optimizing model representation. Pruning and knowledge distillation focus on reducing redundancy in existing models, while NAS addresses how to build optimized architectures from the ground up. Together, they provide a structured framework for understanding how to create machine learning models that are both accurate and computationally efficient. Each of these techniques offers a different approach to improving model efficiency, and in many cases, they can be combined to achieve even greater optimization.

10.4.1 Pruning

State-of-the-art machine learning models often contain millions—or even billions—of parameters, many of which contribute minimally to final predictions. While large models enhance representational power and generalization, they also introduce inefficiencies that impact both training and deployment. From a machine learning systems perspective, these inefficiencies present several challenges:

High Memory Requirements: Large models require substantial storage, limiting their feasibility on resource-constrained devices such as smartphones, IoT devices, and embedded systems. Storing and loading these models also creates bandwidth bottlenecks in distributed ML pipelines.
Increased Computational Cost: More parameters lead to higher inference latency and energy consumption, which is particularly problematic for real-time applications such as autonomous systems, speech recognition, and mobile AI. Running unoptimized models on hardware accelerators like GPUs and TPUs requires additional compute cycles, increasing operational costs.
Scalability Limitations: Training and deploying large models at scale is resource-intensive in terms of compute, memory, and power. Large-scale distributed training demands high-bandwidth communication and storage, while inference in production environments becomes costly without optimizations.

Despite these challenges, not all parameters in a model are necessary to maintain accuracy. Many weights contribute little to the decision-making process, and their removal can significantly improve efficiency without substantial performance degradation. This motivates the use of pruning, a class of optimization techniques that systematically remove redundant parameters while preserving model accuracy.

Definition of Pruning

Pruning is a model optimization technique that removes unnecessary parameters from a neural network while maintaining predictive performance. By systematically eliminating redundant weights, neurons, or layers, pruning reduces model size and computational cost, making it more efficient for storage, inference, and deployment.

Pruning allows models to become smaller, faster, and more efficient without requiring fundamental changes to their architecture. By reducing redundancy, pruning directly addresses the memory, computation, and scalability constraints of machine learning systems, making it a key optimization technique for deploying ML models across cloud, edge, and mobile platforms.

Mathematical Formulation

Pruning can be formally described as an optimization problem, where the goal is to reduce the number of parameters in a neural network while maintaining its predictive performance. Given a trained model with parameters $W$, pruning seeks to find a sparse version of the model, $\hat{W}$, that retains only the most important parameters. The objective can be expressed as:

\[ \min_{\hat{W}} \mathcal{L}(\hat{W}) \quad \text{subject to} \quad \|\hat{W}\|_0 \leq k \]

where:

$\mathcal{L}(\hat{W})$ represents the model’s loss function after pruning.
$\hat{W}$ denotes the pruned model’s parameters.
$\|\hat{W}\|_0$ is the number of nonzero parameters in $\hat{W}$, constrained to a budget $k$.

As illustrated in Figure 10.2, pruning reduces the number of nonzero weights by eliminating small-magnitude values, transforming a dense weight matrix into a sparse representation. This explicit enforcement of sparsity aligns with the $\ell_0$-norm constraint in our optimization formulation.

Figure 10.2: Weight matrix before and after pruning.

However, solving this problem exactly is computationally infeasible due to the discrete nature of the $\ell_0$-norm constraint. Finding the optimal subset of parameters to retain would require evaluating an exponential number of possible parameter configurations, making it impractical for deep networks with millions of parameters (Labarge, n.d.).

To make pruning computationally feasible, practical methods replace the hard constraint on the number of remaining parameters with a soft regularization term that encourages sparsity. A common relaxation is to introduce an $\ell_1$-norm regularization penalty, leading to the following objective:

\[ \min_W \mathcal{L}(W) + \lambda \| W \|_1 \]

where $\lambda$ controls the degree of sparsity. The $\ell_1$-norm encourages smaller weight values and promotes sparsity but does not strictly enforce zero values. Other methods use iterative heuristics, where parameters with the smallest magnitudes are pruned in successive steps, followed by fine-tuning to recover lost accuracy (Gale, Elsen, and Hooker 2019a).

———. 2019a. “The State of Sparsity in Deep Neural Networks.” arXiv Preprint arXiv:1902.09574, February. http://arxiv.org/abs/1902.09574v1.

Structures to Target

Pruning methods vary based on which structures within a neural network are removed. The primary targets include neurons, channels, and layers, each with distinct implications for the model’s architecture and performance.

Neuron pruning removes entire neurons along with their associated weights and biases, reducing the width of a layer. This technique is often applied to fully connected layers.
Channel pruning (or filter pruning), commonly used in convolutional neural networks (CNNs), eliminates entire channels or filters. This reduces the depth of feature maps, which impacts the network’s ability to extract certain features. Channel pruning is particularly valuable in image-processing tasks where computational efficiency is a priority.
Layer pruning removes entire layers from the network, significantly reducing depth. While this approach can yield substantial efficiency gains, it requires careful balance to ensure the model retains sufficient capacity to capture complex patterns.

Figure 10.3 illustrates the differences between channel pruning and layer pruning. When a channel is pruned, the model’s architecture must be adjusted to accommodate the structural change. Specifically, the number of input channels in subsequent layers must be modified, requiring alterations to the depths of the filters applied to the layer with the removed channel. In contrast, layer pruning removes all channels within a layer, necessitating more substantial architectural modifications. In this case, connections between remaining layers must be reconfigured to bypass the removed layer. Regardless of the pruning approach, fine-tuning is essential to adapt the remaining network and restore performance.

Unstructured Pruning

Unstructured pruning reduces the number of active parameters in a neural network by removing individual weights while preserving the overall network architecture. Many machine learning models are overparameterized, meaning they contain more weights than are strictly necessary for accurate predictions. During training, some connections become redundant, contributing little to the final computation. Pruning these weak connections can reduce memory requirements while preserving most of the model’s accuracy.

Mathematically, unstructured pruning introduces sparsity into the weight matrices of a neural network. Let $W \in \mathbb{R}^{m \times n}$ represent a weight matrix in a given layer of a network. Pruning removes a subset of weights by applying a binary mask $M \in \{0,1\}^{m \times n}$, yielding a pruned weight matrix:

\[ \hat{W} = M \odot W \]

where $\odot$ represents the element-wise Hadamard product. The mask $M$ is constructed based on a pruning criterion, typically weight magnitude. A common approach is magnitude-based pruning, which removes a fraction $s$ of the lowest-magnitude weights. This is achieved by defining a threshold $\tau$ such that:

\[ M_{i,j} = \begin{cases} 1, & \text{if } |W_{i,j}| > \tau \\ 0, & \text{otherwise} \end{cases} \]

where $\tau$ is chosen to ensure that only the largest $(1 - s)$ fraction of weights remain. This method assumes that larger-magnitude weights contribute more to the network’s function, making them preferable for retention.

The primary advantage of unstructured pruning is memory efficiency. By reducing the number of nonzero parameters, pruned models require less storage, which is particularly beneficial when deploying models to embedded or mobile devices with limited memory.

However, unstructured pruning does not necessarily improve computational efficiency on modern machine learning hardware. Standard GPUs and TPUs are optimized for dense matrix multiplications, and a sparse weight matrix often cannot fully utilize hardware acceleration unless specialized sparse computation kernels are available. Consequently, unstructured pruning is most beneficial when the goal is to compress a model for storage rather than to accelerate inference speed. While unstructured pruning improves model efficiency at the parameter level, it does not alter the structural organization of the network.

Structured Pruning

While unstructured pruning removes individual weights from a neural network, structured pruning eliminates entire computational units, such as neurons, filters, channels, or layers. This approach is particularly beneficial for hardware efficiency, as it produces smaller dense models that can be directly mapped to modern machine learning accelerators. Unlike unstructured pruning, which results in sparse weight matrices that require specialized execution kernels to exploit computational benefits, structured pruning leads to more efficient inference on general-purpose hardware by reducing the overall size of the network architecture.

Structured pruning is motivated by the observation that not all neurons, filters, or layers contribute equally to a model’s predictions. Some units primarily carry redundant or low-impact information, and removing them does not significantly degrade model performance. The challenge lies in identifying which structures can be pruned while preserving accuracy.

Figure 10.4 illustrates the key differences between unstructured and structured pruning. On the left, unstructured pruning removes individual weights (depicted as dashed connections), leading to a sparse weight matrix. This can disrupt the original structure of the network, as shown in the fully connected network where certain connections have been randomly pruned. While this can reduce the number of active parameters, the resulting sparsity requires specialized execution kernels to fully leverage computational benefits.

In contrast, structured pruning, depicted in the middle and right sections of the figure, removes entire neurons (dashed circles) or filters while preserving the network’s overall structure. In the middle section, a pruned fully connected network retains its fully connected nature but with fewer neurons. On the right, structured pruning is applied to a convolutional neural network (CNN) by removing convolutional kernels or entire channels (dashed squares). This method maintains the CNN’s fundamental convolutional operations while reducing the computational load, making it more compatible with hardware accelerators.

Figure 10.4: Unstructured vs structured pruning. Source: Qi et al. (2021).

A common approach to structured pruning is magnitude-based pruning, where entire neurons or filters are removed based on the magnitude of their associated weights. The intuition behind this method is that parameters with smaller magnitudes contribute less to the model’s output, making them prime candidates for elimination. The importance of a neuron or filter is often measured using a norm function, such as the $\ell_1$-norm or $\ell_2$-norm, applied to the weights associated with that unit. If the norm falls below a predefined threshold, the corresponding neuron or filter is pruned. This method is straightforward to implement and does not require additional computational overhead beyond computing norms across layers.

Another strategy is activation-based pruning, which evaluates the average activation values of neurons or filters over a dataset. Neurons that consistently produce low activations contribute less information to the network’s decision process and can be safely removed. This method captures the dynamic behavior of the network rather than relying solely on static weight values. Activation-based pruning requires profiling the model over a representative dataset to estimate the average activation magnitudes before making pruning decisions.

Gradient-based pruning leverages information from the model’s training process to identify less significant neurons or filters. The key idea is that units with smaller gradient magnitudes contribute less to reducing the loss function, making them less critical for learning. By ranking neurons based on their gradient values, structured pruning can remove those with the least impact on model optimization. Unlike magnitude-based or activation-based pruning, which rely on static properties of the trained model, gradient-based pruning requires access to gradient computations and is typically applied during training rather than as a post-processing step.

Each of these methods presents trade-offs in terms of computational complexity and effectiveness. Magnitude-based pruning is computationally inexpensive and easy to implement but does not account for how neurons behave across different data distributions. Activation-based pruning provides a more data-driven pruning approach but requires additional computations to estimate neuron importance. Gradient-based pruning leverages training dynamics but may introduce additional complexity if applied to large-scale models. The choice of method depends on the specific constraints of the target deployment environment and the performance requirements of the pruned model.

Dynamic Pruning

Traditional pruning methods, whether unstructured or structured, typically involve static pruning, where parameters are permanently removed after training or at fixed intervals during training. However, this approach assumes that the importance of parameters is fixed, which is not always the case. In contrast, dynamic pruning adapts pruning decisions based on the input data or training dynamics, allowing the model to adjust its structure in real time.

Dynamic pruning techniques introduce flexibility into the pruning process by allowing pruned parameters to be reactivated or by adjusting sparsity levels based on usage patterns. Rather than applying a fixed pruning mask, dynamic pruning methods assess the importance of parameters at inference time or throughout training, removing or reinstating them as needed.

One approach to dynamic pruning involves runtime sparsity, where the model determines which weights to use based on the specific input. For example, in activation-conditioned pruning, neurons or channels with low activations for a given input are skipped during computation, leading to input-dependent sparsity. This technique is particularly useful for models deployed in latency-sensitive environments, as it reduces the number of computations required per inference without statically altering the model architecture.

Another class of dynamic pruning operates during training, where sparsity is gradually introduced and adjusted throughout the optimization process. Methods such as gradual magnitude pruning start with a dense network and progressively increase the fraction of pruned parameters as training progresses. Instead of permanently removing parameters, these approaches allow the network to recover from pruning-induced capacity loss by regrowing connections that prove to be important in later stages of training.

Dynamic pruning presents several advantages over static pruning. It allows models to adapt to different workloads, potentially improving efficiency while maintaining accuracy. Unlike static pruning, which risks over-pruning and degrading performance, dynamic pruning provides a mechanism for selectively reactivating parameters when necessary. However, implementing dynamic pruning requires additional computational overhead, as pruning decisions must be made in real-time, either during training or inference. This makes it more complex to integrate into standard machine learning pipelines compared to static pruning.

Despite its challenges, dynamic pruning is particularly useful in edge computing and adaptive AI systems, where resource constraints and real-time efficiency requirements vary across different inputs. The next section explores the practical considerations and trade-offs involved in choosing the right pruning method for a given machine learning system.

Pruning Method Trade-offs

Pruning techniques offer different trade-offs in terms of memory efficiency, computational efficiency, accuracy retention, hardware compatibility, and implementation complexity. The choice of pruning strategy depends on the specific constraints of the machine learning system and the deployment environment.

Unstructured pruning is particularly effective in reducing model size and memory footprint, as it removes individual weights while keeping the overall model architecture intact. However, since machine learning accelerators are optimized for dense matrix operations, unstructured pruning does not always translate to significant computational speed-ups unless specialized sparse execution kernels are used.

Structured pruning, in contrast, eliminates entire neurons, channels, or layers, leading to a more hardware-friendly model. This technique provides direct computational savings, as it reduces the number of floating-point operations (FLOPs) required during inference. The downside is that modifying the network structure can lead to a greater accuracy drop, requiring careful fine-tuning to recover lost performance.

Dynamic pruning introduces adaptability into the pruning process by adjusting which parameters are pruned at runtime based on input data or training dynamics. This allows for a better balance between accuracy and efficiency, as the model retains the flexibility to reintroduce previously pruned parameters if needed. However, dynamic pruning increases implementation complexity, as it requires additional computations to determine which parameters to prune on-the-fly.

Table 10.2 summarizes the key structural differences between these pruning approaches, outlining how each method modifies the model and impacts its execution.

Table 10.2: Comparison of unstructured, structured, and dynamic pruning.

Aspect	Unstructured Pruning	Structured Pruning	Dynamic Pruning
What is removed?	Individual weights in the model	Entire neurons, channels, filters, or layers	Adjusts pruning based on runtime conditions
Model structure	Sparse weight matrices; original architecture remains unchanged	Model architecture is modified; pruned layers are fully removed	Structure adapts dynamically
Impact on memory	Reduces model storage by eliminating nonzero weights	Reduces model storage by removing entire components	Varies based on real-time pruning
Impact on computation	Limited; dense matrix operations still required unless specialized sparse computation is used	Directly reduces FLOPs and speeds up inference	Balances accuracy and efficiency dynamically
Hardware compatibility	Sparse weight matrices require specialized execution support for efficiency	Works efficiently with standard deep learning hardware	Requires adaptive inference engines
Fine-tuning required?	Often necessary to recover accuracy after pruning	More likely to require fine-tuning due to larger structural modifications	Adjusts dynamically, reducing the need for retraining
Use cases	Memory-efficient model compression, particularly for cloud deployment	Real-time inference optimization, mobile/edge AI, and efficient training	Adaptive AI applications, real-time systems

Pruning Execution Strategies

Beyond the broad categories of unstructured, structured, and dynamic pruning, different pruning workflows can impact model efficiency and accuracy retention. Two widely used pruning strategies are iterative pruning and one-shot pruning, each with its own benefits and trade-offs.

Iterative Pruning

Iterative pruning implements a gradual approach to structure removal through multiple cycles of pruning followed by fine-tuning. During each cycle, the algorithm removes a small subset of structures based on predefined importance metrics. The model then undergoes fine-tuning to adapt to these structural modifications before proceeding to the next pruning iteration. This methodical approach helps prevent sudden drops in accuracy while allowing the network to progressively adjust to reduced complexity.

To illustrate this process, consider pruning six channels from a convolutional neural network as shown in Figure 10.5. Rather than removing all channels simultaneously, iterative pruning eliminates two channels per iteration over three cycles. Following each pruning step, the model undergoes fine-tuning to recover performance. The first iteration, which removes two channels, results in an accuracy decrease from 0.995 to 0.971, but subsequent fine-tuning restores accuracy to 0.992. After completing two additional pruning-tuning cycles, the final model achieves 0.991 accuracy—representing only a 0.4% reduction from the original—while operating with 27% fewer channels. By distributing structural modifications across multiple iterations, the network maintains its performance capabilities while achieving improved computational efficiency.

One-shot Pruning

One-shot pruning removes multiple architectural components in a single step, followed by an extensive fine-tuning phase to recover model accuracy. This aggressive approach compresses the model quickly but risks greater accuracy degradation, as the network must adapt to substantial structural changes simultaneously.

Consider applying one-shot pruning to the same network discussed in the iterative pruning example. Instead of removing two channels at a time over multiple iterations, one-shot pruning eliminates all six channels at once, as illustrated in Figure 10.6. Removing 27% of the network’s channels simultaneously causes the accuracy to drop significantly, from 0.995 to 0.914. Even after fine-tuning, the network only recovers to an accuracy of 0.943, which is a 5% degradation from the original unpruned network. While both iterative and one-shot pruning ultimately produce identical network structures, the gradual approach of iterative pruning better preserves model performance.

The choice of pruning strategy requires careful consideration of several key factors that influence both model efficiency and performance:

Sparsity Target: The desired level of parameter reduction directly impacts strategy selection. Higher reduction targets often necessitate iterative approaches to maintain accuracy, while moderate sparsity goals may be achievable through simpler one-shot methods. Computational Resources: Available computing power significantly influences strategy choice. Iterative pruning demands substantial resources for multiple fine-tuning cycles, whereas one-shot approaches require fewer resources but may sacrifice accuracy. Performance Requirements: Applications with strict accuracy requirements typically benefit from gradual, iterative pruning to carefully preserve model capabilities. Use cases with more flexible performance constraints may accommodate more aggressive one-shot approaches. Development Timeline: Project schedules impact pruning decisions. One-shot methods enable faster deployment when time is limited, though iterative approaches generally achieve superior results given sufficient optimization periods. Hardware Constraints: Target platform capabilities significantly influence strategy selection. Certain hardware architectures may better support specific sparsity patterns, making particular pruning approaches more advantageous for deployment.

The choice between pruning strategies requires careful evaluation of project requirements and constraints. One-shot pruning enables rapid model compression by removing multiple parameters simultaneously, making it suitable for scenarios where deployment speed is prioritized over accuracy. However, this aggressive approach often results in greater performance degradation compared to more gradual methods. Iterative pruning, on the other hand, while computationally intensive and time-consuming, typically achieves superior accuracy retention through systematic parameter reduction across multiple cycles. This methodical approach enables the network to adapt progressively to structural modifications, preserving critical connections that maintain model performance. The trade-off is increased optimization time and computational overhead. By evaluating these factors systematically, practitioners can select a pruning approach that optimally balances efficiency gains with model performance for their specific use case.

The Lottery Ticket Hypothesis

Pruning is widely used to reduce the size and computational cost of neural networks, but the process of determining which parameters to remove is not always straightforward. While traditional pruning methods eliminate weights based on magnitude, structure, or dynamic conditions, recent research suggests that pruning is not just about reducing redundancy—it may also reveal inherently efficient subnetworks that exist within the original model.

This perspective leads to the Lottery Ticket Hypothesis (LTH), which challenges conventional pruning workflows by proposing that within large neural networks, there exist small, well-initialized subnetworks—“winning tickets”—that can achieve comparable accuracy to the full model when trained in isolation. Rather than viewing pruning as just a post-training compression step, LTH suggests it can serve as a discovery mechanism to identify these efficient subnetworks early in training.

LTH is validated through an iterative pruning process, illustrated in Figure 10.7. A large network is first trained to convergence. The lowest-magnitude weights are then pruned, and the remaining weights are reset to their original initialization rather than being re-randomized. This process is repeated iteratively, gradually reducing the network’s size while preserving performance. After multiple iterations, the remaining subnetwork—the “winning ticket”—proves capable of training to the same or higher accuracy as the original full model.

Figure 10.7: The lottery ticket hypothesis.

The implications of the Lottery Ticket Hypothesis extend beyond conventional pruning techniques. Instead of training large models and pruning them later, LTH suggests that compact, high-performing subnetworks could be trained directly from the start, eliminating the need for overparameterization. This insight challenges the traditional assumption that model size is necessary for effective learning. It also emphasizes the importance of initialization, as winning tickets only retain their performance when reset to their original weight values. This finding raises deeper questions about the role of initialization in shaping a network’s learning trajectory.

The hypothesis further reinforces the effectiveness of iterative pruning over one-shot pruning. Gradually refining the model structure allows the network to adapt at each stage, preserving accuracy more effectively than removing large portions of the model in a single step. This process aligns well with practical pruning strategies used in deployment, where preserving accuracy while reducing computation is critical.

Despite its promise, applying LTH in practice remains computationally expensive, as identifying winning tickets requires multiple cycles of pruning and retraining. Ongoing research explores whether winning subnetworks can be detected early without full training, potentially leading to more efficient sparse training techniques. If such methods become practical, LTH could fundamentally reshape how machine learning models are trained, shifting the focus from pruning large networks after training to discovering and training only the essential components from the beginning.

While LTH presents a compelling theoretical perspective on pruning, practical implementations rely on established framework-level tools to integrate structured and unstructured pruning techniques.

Pruning in Practice

Several machine learning frameworks provide built-in tools to apply structured and unstructured pruning, fine-tune pruned models, and optimize deployment for cloud, edge, and mobile environments.

Machine learning frameworks such as PyTorch, TensorFlow, and ONNX offer dedicated pruning utilities that allow practitioners to efficiently implement these techniques while ensuring compatibility with deployment hardware.

In PyTorch, pruning is available through the torch.nn.utils.prune module, which provides functions to apply magnitude-based pruning to individual layers or the entire model. Users can perform unstructured pruning by setting a fraction of the smallest-magnitude weights to zero or apply structured pruning to remove entire neurons or filters. PyTorch also allows for custom pruning strategies, where users define pruning criteria beyond weight magnitude, such as activation-based or gradient-based pruning. Once a model is pruned, it can be fine-tuned to recover lost accuracy before being exported for inference.

TensorFlow provides pruning support through the TensorFlow Model Optimization Toolkit (TF-MOT). This toolkit integrates pruning directly into the training process by applying sparsity-inducing regularization. TensorFlow’s pruning API supports global and layer-wise pruning, dynamically selecting parameters for removal based on weight magnitudes. Unlike PyTorch, TensorFlow’s pruning is typically applied during training, allowing models to learn sparse representations from the start rather than pruning them post-training. TF-MOT also provides export tools to convert pruned models into TFLite format, making them compatible with mobile and edge devices.

ONNX, an open standard for model representation, does not implement pruning directly but provides export and compatibility support for pruned models from PyTorch and TensorFlow. Since ONNX is designed to be hardware-agnostic, it allows models that have undergone pruning in different frameworks to be optimized for inference engines such as TensorRT, OpenVINO, and EdgeTPU. These inference engines can further leverage structured and dynamic pruning for execution efficiency, particularly on specialized hardware accelerators.

Although framework-level support for pruning has advanced significantly, applying pruning in practice requires careful consideration of hardware compatibility and software optimizations. Standard CPUs and GPUs often do not natively accelerate sparse matrix operations, meaning that unstructured pruning may reduce memory usage without providing significant computational speed-ups. In contrast, structured pruning is more widely supported in inference engines, as it directly reduces the number of computations needed during execution. Dynamic pruning, when properly integrated with inference engines, can optimize execution based on workload variations and hardware constraints, making it particularly beneficial for adaptive AI applications.

At a practical level, choosing the right pruning strategy depends on several key trade-offs, including memory efficiency, computational performance, accuracy retention, and implementation complexity. These trade-offs impact how pruning methods are applied in real-world machine learning workflows, influencing deployment choices based on resource constraints and system requirements.

To help guide these decisions, Table 10.3 provides a high-level comparison of these trade-offs, summarizing the key efficiency and usability factors that practitioners must consider when selecting a pruning method.

Table 10.3: Comparison of pruning strategies.

Criterion	Unstructured Pruning	Structured Pruning	Dynamic Pruning
Memory Efficiency	↑↑ High	↑ Moderate	↑ Moderate
Computational Efficiency	→ Neutral	↑↑ High	↑ High
Accuracy Retention	↑ Moderate	↓↓ Low	↑↑ High
Hardware Compatibility	↓ Low	↑↑ High	→ Neutral
Implementation Complexity	→ Neutral	↑ Moderate	↓↓ High

These trade-offs underscore the importance of aligning pruning methods with practical deployment needs. Frameworks such as PyTorch, TensorFlow, and ONNX enable developers to implement these strategies, but the effectiveness of a pruning approach depends on the underlying hardware and application requirements.

For example, structured pruning is commonly used in mobile and edge applications because of its compatibility with standard inference engines, whereas dynamic pruning is better suited for adaptive AI workloads that need to adjust sparsity levels on the fly. Unstructured pruning, while useful for reducing memory footprints, requires specialized sparse execution kernels to fully realize computational savings.

Understanding these trade-offs is essential when deploying pruned models in real-world settings. Several high-profile models have successfully integrated pruning to optimize performance. MobileNet, a lightweight convolutional neural network designed for mobile and embedded applications, has been pruned to reduce inference latency while preserving accuracy (Howard et al. 2017). BERT, a widely used transformer model for natural language processing, has undergone structured pruning of attention heads and intermediate layers to create efficient versions such as DistilBERT and TinyBERT, which retain much of the original performance while reducing computational overhead (Sanh et al. 2019). In computer vision, EfficientNet has been pruned to remove unnecessary filters, optimizing it for deployment in resource-constrained environments (Tan and Le 2019a).

Howard, Andrew G., Menglong Zhu, Bo Chen, Dmitry Kalenichenko, Weijun Wang, Tobias Weyand, Marco Andreetto, and Hartwig Adam. 2017. “MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications.” ArXiv Preprint abs/1704.04861 (April). http://arxiv.org/abs/1704.04861v1.

10.4.2 Knowledge Distillation

Machine learning models are often trained with the goal of achieving the highest possible accuracy, leading to the development of large, complex architectures with millions or even billions of parameters. While these models excel in performance, they are computationally expensive and difficult to deploy in resource-constrained environments such as mobile devices, edge computing platforms, and real-time inference systems. Knowledge distillation is a technique designed to transfer the knowledge of a large, high-capacity model (the teacher) into a smaller, more efficient model (the student) while preserving most of the original model’s performance (Gou et al. 2021).

Lin, Jiong, Qing Gao, Yungui Gong, Yizhou Lu, Chao Zhang, and Fengge Zhang. 2020. “Primordial Black Holes and Secondary Gravitational Waves from k/g Inflation.” arXiv Preprint arXiv:2001.05909, January. http://arxiv.org/abs/2001.05909v2.

Unlike pruning, which removes unnecessary parameters from a trained model, knowledge distillation involves training a separate, smaller model using guidance from a larger pre-trained model. The student model does not simply learn from labeled data but instead is optimized to match the soft predictions of the teacher model (Jiong Lin et al. 2020). These soft targets—probability distributions over classes rather than hard labels—contain richer information about how the teacher model generalizes beyond just the correct answer, helping the student learn more efficiently.

As illustrated in Figure 10.8, the knowledge distillation process involves two models: a high-capacity teacher model (top) and a smaller student model (bottom). The teacher model is first trained on the given dataset and produces a probability distribution over classes using a softened softmax function with temperature $T$. These soft labels encode more information than traditional hard labels by capturing the relative similarities between different classes. The student model is trained using both these soft labels and the ground truth hard labels.

The training process for the student model incorporates two loss terms:

Distillation loss: A loss function (often based on Kullback-Leibler (KL) divergence) that minimizes the difference between the student’s and teacher’s soft label distributions.
Student loss: A standard cross-entropy loss that ensures the student model correctly classifies the hard labels.

The combination of these two loss functions enables the student model to absorb both structured knowledge from the teacher and label supervision from the dataset. This approach allows smaller models to reach accuracy levels close to their larger teacher models, making knowledge distillation a key technique for model compression and efficient deployment.

Knowledge distillation allows smaller models to reach a level of accuracy that would be difficult to achieve through standard training alone. This makes it particularly useful in ML systems where inference efficiency is a priority, such as real-time applications, cloud-to-edge model compression, and low-power AI systems (Sun et al. 2019).

Sun, Siqi, Yu Cheng, Zhe Gan, and Jingjing Liu. 2019. “Patient Knowledge Distillation for BERT Model Compression.” In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP). Association for Computational Linguistics. https://doi.org/10.18653/v1/d19-1441.

Theoretical Foundation

Knowledge distillation is based on the idea that a well-trained teacher model encodes more information about the data distribution than just the correct class labels. In conventional supervised learning, a model is trained to minimize the cross-entropy loss between its predictions and the ground truth labels. However, this approach only provides a hard decision boundary for each class, discarding potentially useful information about how the model relates different classes to one another (Hinton, Vinyals, and Dean 2015).

Hinton, Geoffrey, Oriol Vinyals, and Jeff Dean. 2015. “Distilling the Knowledge in a Neural Network,” March. https://doi.org/10.1002/0471743984.vse0673.

Gou, Jianping, Baosheng Yu, Stephen J. Maybank, and Dacheng Tao. 2021. “Knowledge Distillation: A Survey.” International Journal of Computer Vision 129 (6): 1789–819. https://doi.org/10.1007/s11263-021-01453-z.

In contrast, knowledge distillation transfers this additional information by using the soft probability distributions produced by the teacher model. Instead of training the student model to match only the correct label, it is trained to match the teacher’s full probability distribution over all possible classes. This is achieved by introducing a temperature-scaled softmax function, which smooths the probability distribution, making it easier for the student model to learn from the teacher’s outputs (Gou et al. 2021).

Mathematical Formulation

Let $z_i$ be the logits (pre-softmax outputs) of the model for class $i$. The standard softmax function computes class probabilities as:

\[ p_i = \frac{\exp(z_i)}{\sum_j \exp(z_j)} \]

where higher logits correspond to higher confidence in a class prediction.

In knowledge distillation, we introduce a temperature parameter $T$ that scales the logits before applying softmax:

\[ p_i(T) = \frac{\exp(z_i / T)}{\sum_j \exp(z_j / T)} \]

where a higher temperature produces a softer probability distribution, revealing more information about how the model distributes uncertainty across different classes.

The student model is then trained using a loss function that minimizes the difference between its output distribution and the teacher’s softened output distribution. The most common formulation combines two loss terms:

\[ \mathcal{L}_{\text{distill}} = (1 - \alpha) \mathcal{L}_{\text{CE}}(y_s, y) + \alpha T^2 \sum_i p_i^T \log p_{i, s}^T \]

where:

$\mathcal{L}_{\text{CE}}(y_s, y)$ is the standard cross-entropy loss between the student’s predictions $y_s$ and the ground truth labels $y$.
The second term minimizes the Kullback-Leibler (KL) divergence between the teacher’s softened predictions $p_i^T$ and the student’s predictions $p_{i, s}^T$.
The factor $T^2$ ensures that gradients remain appropriately scaled when using high-temperature values.
The hyperparameter $\alpha$ balances the importance of the standard training loss versus the distillation loss.

Intuition Behind Why Distillation Works

By learning from both hard labels and soft teacher outputs, the student model benefits from the generalization power of the teacher, improving its ability to distinguish between similar classes even with fewer parameters. Unlike conventional training, where a model learns only from binary correctness signals, knowledge distillation allows the student to absorb a richer understanding of the data distribution from the teacher’s predictions.

A key advantage of soft targets is that they provide relative confidence levels rather than just a single correct answer. Consider an image classification task where the goal is to distinguish between different animal species. A standard model trained with hard labels will only receive feedback on whether its prediction is right or wrong. If an image contains a cat, the correct label is “cat,” and all other categories, such as “dog” and “fox,” are treated as equally incorrect. However, a well-trained teacher model naturally understands that a cat is more visually similar to a dog than to a fox, and its soft output probabilities might look like Figure 10.9, where the relative confidence levels indicate that while “cat” is the most likely category, “dog” is still a plausible alternative, whereas “fox” is much less likely.

Figure 10.9: Soft target probability distribution.

Rather than simply forcing the student model to classify the image strictly as a cat, the teacher model provides a more nuanced learning signal, indicating that while “dog” is incorrect, it is a more reasonable mistake than “fox.” This subtle information helps the student model build better decision boundaries between similar classes, making it more robust to ambiguity in real-world data.

This effect is particularly useful in cases where training data is limited or noisy. A large teacher model trained on extensive data has already learned to generalize well, capturing patterns that might be difficult to discover with smaller datasets. The student benefits by inheriting this structured knowledge, acting as if it had access to a larger training signal than what is explicitly available.

Another key benefit of knowledge distillation is its regularization effect. Because soft targets distribute probability mass across multiple classes, they prevent the student model from overfitting to specific hard labels. Instead of confidently assigning a probability of 1.0 to the correct class and 0.0 to all others, the student learns to make more calibrated predictions, which improves its generalization performance. This is especially important when the student model has fewer parameters, as smaller networks are more prone to overfitting.

Finally, distillation helps compress large models into smaller, more efficient versions without major performance loss. Training a small model from scratch often results in lower accuracy because the model lacks the capacity to learn the complex representations that a larger network can capture. However, by leveraging the knowledge of a well-trained teacher, the student can reach a higher accuracy than it would have on its own, making it a more practical choice for real-world ML deployments, particularly in edge computing, mobile applications, and other resource-constrained environments.

Efficiency Gains

Knowledge distillation is widely used in machine learning systems because it enables smaller models to achieve performance levels comparable to larger models, making it an essential technique for optimizing inference efficiency. While pruning reduces the size of a trained model by removing unnecessary parameters, knowledge distillation improves efficiency by training a compact model from the start, leveraging the teacher’s guidance to enhance learning (Sanh et al. 2019). This allows the student model to reach a level of accuracy that would be difficult to achieve through standard training alone.

Sanh, Victor, Lysandre Debut, Julien Chaumond, and Thomas Wolf. 2019. “DistilBERT, a Distilled Version of BERT: Smaller, Faster, Cheaper and Lighter.” arXiv Preprint arXiv:1910.01108, October. http://arxiv.org/abs/1910.01108v4.

The efficiency benefits of knowledge distillation can be categorized into three key areas: memory efficiency, computational efficiency, and deployment flexibility.

Memory Efficiency and Model Compression

A key advantage of knowledge distillation is that it enables smaller models to retain much of the predictive power of larger models, significantly reducing memory footprint. This is particularly useful in resource-constrained environments such as mobile and embedded AI systems, where model size directly impacts storage requirements and load times.

For instance, models such as DistilBERT in NLP and MobileNet distillation variants in computer vision have been shown to retain up to 97% of the accuracy of their larger teacher models while using only half the number of parameters. This level of compression is often superior to pruning, where aggressive parameter reduction can lead to deterioration in representational power.

Another key benefit of knowledge distillation is its ability to transfer robustness and generalization from the teacher to the student. Large models are often trained with extensive datasets and develop strong generalization capabilities, meaning they are less sensitive to noise and data shifts. A well-trained student model inherits these properties, making it less prone to overfitting and more stable across diverse deployment conditions. This is particularly useful in low-data regimes, where training a small model from scratch may result in poor generalization due to insufficient training examples.

Computational Efficiency and Inference Speed

By training the student model to approximate the teacher’s knowledge in a more compact representation, distillation results in models that require fewer FLOPs per inference, leading to faster execution times. Unlike unstructured pruning, which may require specialized hardware support for sparse computation, a distilled model remains densely structured, making it more compatible with existing machine learning accelerators such as GPUs, TPUs, and edge AI chips (Jiao et al. 2020).

Jiao, Xiaoqi, Yichun Yin, Lifeng Shang, Xin Jiang, Xiao Chen, Linlin Li, Fang Wang, and Qun Liu. 2020. “TinyBERT: Distilling BERT for Natural Language Understanding.” In Findings of the Association for Computational Linguistics: EMNLP 2020. Association for Computational Linguistics. https://doi.org/10.18653/v1/2020.findings-emnlp.372.

In real-world deployments, this translates to:

Reduced inference latency, which is important for real-time AI applications such as speech recognition, recommendation systems, and self-driving perception models.
Lower energy consumption, making distillation particularly relevant for low-power AI on mobile devices and IoT systems.
Higher throughput in cloud inference, where serving a distilled model allows large-scale AI applications to reduce computational cost while maintaining model quality.

For example, when deploying transformer models for NLP, organizations often use teacher-student distillation to create models that achieve similar accuracy at 2-4× lower latency, making it feasible to serve billions of requests per day with significantly lower computational overhead.

Deployment Flexibility and System-Level Considerations

Knowledge distillation is also effective in multi-task learning scenarios, where a single teacher model can guide multiple student models for different tasks. For example, in multi-lingual NLP models, a large teacher trained on multiple languages can transfer language-specific knowledge to smaller, task-specific student models, enabling efficient deployment across different languages without retraining from scratch. Similarly, in computer vision, a teacher trained on diverse object categories can distill knowledge into specialized students optimized for tasks such as face recognition, medical imaging, or autonomous driving.

Once a student model is distilled, it can be further optimized for hardware-specific acceleration using techniques such as pruning, quantization, and graph optimization. This ensures that compressed models remain inference-efficient across multiple hardware environments, particularly in edge AI and mobile deployments (Gordon, Duh, and Andrews 2020).

Gordon, Mitchell, Kevin Duh, and Nicholas Andrews. 2020. “Compressing BERT: Studying the Effects of Weight Pruning on Transfer Learning.” In Proceedings of the 5th Workshop on Representation Learning for NLP. Association for Computational Linguistics. https://doi.org/10.18653/v1/2020.repl4nlp-1.18.

Despite its advantages, knowledge distillation has some limitations. The effectiveness of distillation depends on the quality of the teacher model—a poorly trained teacher may transfer incorrect biases to the student. Additionally, distillation introduces an additional training phase, where both the teacher and student must be used together, increasing computational costs during training. In some cases, designing an appropriate student model architecture that can fully benefit from the teacher’s knowledge remains a challenge, as overly small student models may not have enough capacity to absorb all the relevant information.

Trade-offs

Knowledge distillation is a powerful technique for compressing large models into smaller, more efficient versions while maintaining accuracy. By training a student model under the supervision of a teacher model, distillation enables better generalization and inference efficiency compared to training a small model from scratch. It is particularly effective in low-resource environments, such as mobile devices, edge AI, and large-scale cloud inference, where balancing accuracy, speed, and memory footprint is essential.

Compared to pruning, distillation preserves accuracy better but comes at the cost of higher training complexity, as it requires training a new model instead of modifying an existing one. However, pruning provides a more direct computational efficiency gain, especially when structured pruning is used. In practice, combining pruning and distillation often yields the best trade-off, as seen in models like DistilBERT and MobileBERT, where pruning first reduces unnecessary parameters before distillation optimizes a final student model. Table 10.4 summarizes the key trade-offs between knowledge distillation and pruning.

Table 10.4: Comparison of knowledge distillation and pruning.

Criterion	Knowledge Distillation	Pruning
Accuracy retention	High – Student learns from teacher, better generalization	Varies – Can degrade accuracy if over-pruned
Training cost	Higher – Requires training both teacher and student	Lower – Only fine-tuning needed
Inference speed	High – Produces dense, optimized models	Depends – Structured pruning is efficient, unstructured needs special support
Hardware compatibility	High – Works on standard accelerators	Limited – Sparse models may need specialized execution
Ease of implementation	Complex – Requires designing a teacher-student pipeline	Simple – Applied post-training

Knowledge distillation remains an essential technique in ML systems optimization, often used alongside pruning and quantization for deployment-ready models. The next section explores quantization, a method that further reduces computational cost by lowering numerical precision.

10.4.3 Structured Approximations

Machine learning models often contain a significant degree of parameter redundancy, leading to inefficiencies in computation, storage, and energy consumption. The preceding sections on pruning and knowledge distillation introduced methods that explicitly remove redundant parameters or transfer knowledge to a smaller model. In contrast, approximation-based compression techniques focus on restructuring model representations to reduce complexity while maintaining expressive power.

Rather than eliminating individual parameters, approximation methods decompose large weight matrices and tensors into lower-dimensional components, allowing models to be stored and executed more efficiently. These techniques leverage the observation that many high-dimensional representations can be well-approximated by lower-rank structures, thereby reducing the number of parameters without a substantial loss in performance. Unlike pruning, which selectively removes connections, or distillation, which transfers learned knowledge, factorization-based approaches optimize the internal representation of a model through structured approximations.

Among the most widely used approximation techniques are:

Low-Rank Matrix Factorization (LRMF): A method for decomposing weight matrices into products of lower-rank matrices, reducing storage and computational complexity.
Tensor Decomposition: A generalization of LRMF to higher-dimensional tensors, enabling more efficient representations of multi-way interactions in neural networks.

These methods have been widely applied in machine learning to improve model efficiency, particularly in resource-constrained environments such as edge ML and Tiny ML. Additionally, they play a key role in accelerating model training and inference by reducing the number of required operations. The following sections will provide a detailed examination of low-rank matrix factorization and tensor decomposition, including their mathematical foundations, applications, and associated trade-offs.

Low-Rank Matrix Factorization

Many machine learning models contain a significant degree of redundancy in their weight matrices, leading to inefficiencies in computation, storage, and deployment. In the previous sections, pruning and knowledge distillation were introduced as methods to reduce model size—pruning by selectively removing parameters and distillation by transferring knowledge from a larger model to a smaller one. However, these techniques do not fundamentally alter the structure of the model’s parameters. Instead, they focus on reducing redundant weights or optimizing training processes.

Low-Rank Matrix Factorization (LRMF) provides an alternative approach by approximating a model’s weight matrices with lower-rank representations, rather than explicitly removing or transferring information. This technique restructures large parameter matrices into compact, lower-dimensional components, preserving most of the original information while significantly reducing storage and computational costs. Unlike pruning, which creates sparse representations, or distillation, which requires an additional training process, LRMF is a purely mathematical transformation that decomposes a weight matrix into two or more smaller matrices.

This structured compression is particularly useful in machine learning systems where efficiency is a primary concern, such as edge computing, cloud inference, and hardware-accelerated ML execution. By leveraging low-rank approximations, models can achieve substantial reductions in parameter storage while maintaining predictive accuracy, making LRMF a valuable tool for optimizing machine learning architectures.

Mathematical Formulation

Low-rank matrix factorization (LRMF) is a mathematical technique used in linear algebra and machine learning systems to approximate a high-dimensional matrix by decomposing it into the product of lower-dimensional matrices. This factorization enables a more compact representation of model parameters, reducing both memory footprint and computational complexity while preserving essential structural information. In the context of machine learning systems, LRMF plays a crucial role in optimizing model efficiency, particularly for resource-constrained environments such as edge AI and embedded deployments.

Formally, given a matrix $A \in \mathbb{R}^{m \times n}$, LRMF seeks two matrices $U \in \mathbb{R}^{m \times k}$ and $V \in \mathbb{R}^{k \times n}$ such that:

\[ A \approx UV \]

where $k$ is the rank of the approximation, typically much smaller than both $m$ and $n$. This approximation is commonly obtained through singular value decomposition (SVD), where $A$ is factorized as:

\[ A = U \Sigma V^T \]

where $\Sigma$ is a diagonal matrix containing singular values, and $U$ and $V$ are orthogonal matrices. By retaining only the top $k$ singular values, a low-rank approximation of $A$ is obtained.

Figure 10.10 illustrates the decrease in parameterization enabled by low-rank matrix factorization. Observe how the matrix $M$ can be approximated by the product of matrices $L_k$ and $R_k^T$. For intuition, most fully connected layers in networks are stored as a projection matrix $M$, which requires $m \times n$ parameters to be loaded during computation. However, by decomposing and approximating it as the product of two lower-rank matrices, we only need to store $m \times k + k \times n$ parameters in terms of storage while incurring an additional compute cost of the matrix multiplication. So long as $k < n/2$, this factorization has fewer total parameters to store while adding a computation of runtime $O(mkn)$ (Gu 2023).

Gu, Ivy. 2023. “Deep Learning Model Compression (Ii) by Ivy Gu Medium.” https://ivygdy.medium.com/deep-learning-model-compression-ii-546352ea9453.

Figure 10.10: Low matrix factorization. Source: The Clever Machine.

LRMF is widely used to enhance the efficiency of machine learning models by reducing parameter redundancy, particularly in fully connected and convolutional layers. In the broader context of machine learning systems, factorization techniques contribute to optimizing model inference speed, storage efficiency, and adaptability to specialized hardware accelerators.

Fully connected layers often contain large weight matrices, making them ideal candidates for factorization. Instead of storing a dense $m \times n$ weight matrix, LRMF allows for a more compact representation with two smaller matrices of dimensions $m \times k$ and $k \times n$, significantly reducing storage and computational costs. This reduction is particularly valuable in cloud-to-edge ML pipelines, where minimizing model size can facilitate real-time execution on embedded devices.

Convolutional layers can also benefit from LRMF by decomposing convolutional filters into separable structures. Techniques such as depthwise-separable convolutions leverage factorization principles to achieve computational efficiency without significant loss in accuracy. These methods align well with hardware-aware optimizations used in modern AI acceleration frameworks.

LRMF has been extensively used in collaborative filtering for recommendation systems. By factorizing user-item interaction matrices, latent factors corresponding to user preferences and item attributes can be extracted, enabling efficient and accurate recommendations. Within large-scale machine learning systems, such optimizations directly impact scalability and performance in production environments.

Efficiency Gains and Challenges

By factorizing a weight matrix into lower-rank components, the number of parameters required for storage is reduced from $O(mn)$ to $O(mk + kn)$, where $k$ is significantly smaller than $m, n$. However, this reduction comes at the cost of an additional matrix multiplication operation during inference, potentially increasing computational latency. In machine learning systems, this trade-off is carefully managed to balance storage efficiency and real-time inference speed.

Choosing an appropriate rank $k$ is a key challenge in LRMF. A smaller $k$ results in greater compression but may lead to significant information loss, while a larger $k$ retains more information but offers limited efficiency gains. Methods such as cross-validation and heuristic approaches are often employed to determine the optimal rank, particularly in large-scale ML deployments where compute and storage constraints vary.

In real-world machine learning applications, datasets may contain noise or missing values, which can affect the quality of factorization. Regularization techniques, such as adding an $L_2$ penalty, can help mitigate overfitting and improve the robustness of LRMF, ensuring stable performance across different ML system architectures.

Low-rank matrix factorization provides an effective approach for reducing the complexity of machine learning models while maintaining their expressive power. By approximating weight matrices with lower-rank representations, LRMF facilitates efficient inference and model deployment, particularly in resource-constrained environments such as edge computing. Within machine learning systems, factorization techniques contribute to scalable, hardware-aware optimizations that enhance real-world model performance. Despite challenges such as rank selection and computational overhead, LRMF remains a valuable tool for improving efficiency in ML system design and deployment.

Tensor Decomposition

While low-rank matrix factorization provides an effective method for compressing large weight matrices in machine learning models, many modern architectures rely on multi-dimensional tensors rather than two-dimensional matrices. Convolutional layers, attention mechanisms, and embedding representations commonly involve multi-way interactions that cannot be efficiently captured using standard matrix factorization techniques. In such cases, tensor decomposition provides a more general approach to reducing model complexity while preserving structural relationships within the data.

Tensor decomposition (TD) extends the principles of low-rank factorization to higher-order tensors, allowing large multi-dimensional arrays to be expressed in terms of lower-rank components (see Figure 10.11). Given that tensors frequently appear in machine learning systems as representations of weight parameters, activations, and input features, their direct storage and computation often become impractical. By decomposing these tensors into a set of smaller factors, tensor decomposition significantly reduces memory requirements and computational overhead while maintaining the integrity of the original structure.

Figure 10.11: Tensor decomposition. Source: Richter and Zhao (2021).

This approach is widely used in machine learning to improve efficiency across various architectures. In convolutional neural networks, tensor decomposition enables the approximation of convolutional kernels with lower-dimensional factors, reducing the number of parameters while preserving the representational power of the model. In natural language processing, high-dimensional embeddings can be factorized into more compact representations, leading to faster inference and reduced memory consumption. In hardware acceleration, tensor decomposition helps optimize tensor operations for execution on specialized processors, ensuring efficient utilization of computational resources.

Mathematical Formulation

A tensor is a multi-dimensional extension of a matrix, representing data across multiple axes rather than being confined to two-dimensional structures. In machine learning, tensors naturally arise in various contexts, including the representation of weight parameters, activations, and input features. Given the high dimensionality of these tensors, direct storage and computation often become impractical, necessitating efficient factorization techniques.

Tensor decomposition generalizes the principles of low-rank matrix factorization by approximating a high-order tensor with a set of lower-rank components. Formally, for a given tensor $\mathcal{A} \in \mathbb{R}^{m \times n \times p}$, the goal of decomposition is to express $\mathcal{A}$ in terms of factorized components that require fewer parameters to store and manipulate. This decomposition reduces the memory footprint and computational requirements while retaining the structural relationships present in the original tensor.

Several factorization methods have been developed for tensor decomposition, each suited to different applications in machine learning. One common approach is CANDECOMP/PARAFAC (CP) decomposition, which expresses a tensor as a sum of rank-one components. In CP decomposition, a tensor $\mathcal{A} \in \mathbb{R}^{m \times n \times p}$ is approximated as

\[ \mathcal{A} \approx \sum_{r=1}^{k} u_r \otimes v_r \otimes w_r \]

where $u_r \in \mathbb{R}^{m}$, $v_r \in \mathbb{R}^{n}$, and $w_r \in \mathbb{R}^{p}$ are factor vectors and $k$ is the rank of the approximation.

Another widely used approach is Tucker decomposition, which generalizes singular value decomposition to tensors by introducing a core tensor $\mathcal{G} \in \mathbb{R}^{k_1 \times k_2 \times k_3}$ and factor matrices $U \in \mathbb{R}^{m \times k_1}$, $V \in \mathbb{R}^{n \times k_2}$, and $W \in \mathbb{R}^{p \times k_3}$, such that

\[ \mathcal{A} \approx \mathcal{G} \times_1 U \times_2 V \times_3 W \]

where $\times_i$ denotes the mode-$i$ tensor-matrix multiplication.

Another method, Tensor-Train (TT) decomposition, factorizes high-order tensors into a sequence of lower-rank matrices, reducing both storage and computational complexity. Given a tensor $\mathcal{A} \in \mathbb{R}^{m_1 \times m_2 \times \dots \times m_d}$, TT decomposition represents it as a product of lower-dimensional tensor cores $\mathcal{G}^{(i)}$, where each core $\mathcal{G}^{(i)}$ has dimensions $\mathbb{R}^{r_{i-1} \times m_i \times r_i}$, and the full tensor is reconstructed as

\[ \mathcal{A} \approx \mathcal{G}^{(1)} \times \mathcal{G}^{(2)} \times \dots \times \mathcal{G}^{(d)} \]

where $r_i$ are the TT ranks.

These tensor decomposition methods play a crucial role in optimizing machine learning models by reducing parameter redundancy while maintaining expressive power. The next section will examine how these techniques are applied to machine learning architectures and discuss their computational trade-offs.

Applications of TD

Tensor decomposition methods are widely applied in machine learning systems to improve efficiency and scalability. By factorizing high-dimensional tensors into lower-rank representations, these methods reduce memory usage and computational requirements while preserving the model’s expressive capacity. This section examines several key applications of tensor decomposition in machine learning, focusing on its impact on convolutional neural networks, natural language processing, and hardware acceleration.

In convolutional neural networks (CNNs), tensor decomposition is used to compress convolutional filters and reduce the number of required operations during inference. A standard convolutional layer contains a set of weight tensors that define how input features are transformed. These weight tensors often exhibit redundancy, meaning they can be decomposed into smaller components without significantly degrading performance. Techniques such as CP decomposition and Tucker decomposition enable convolutional filters to be approximated using lower-rank tensors, reducing the number of parameters and computational complexity of the convolution operation. This form of structured compression is particularly valuable in edge and mobile machine learning applications, where memory and compute resources are constrained.

In natural language processing (NLP), tensor decomposition is commonly applied to embedding layers and attention mechanisms. Many NLP models, including transformers, rely on high-dimensional embeddings to represent words, sentences, or entire documents. These embeddings can be factorized using tensor decomposition to reduce storage requirements without compromising their ability to capture semantic relationships. Similarly, in transformer-based architectures, the self-attention mechanism requires large tensor multiplications, which can be optimized using decomposition techniques to lower the computational burden and accelerate inference.

Hardware acceleration for machine learning also benefits from tensor decomposition by enabling more efficient execution on specialized processors such as graphics processing units (GPUs), tensor processing units (TPUs), and field-programmable gate arrays (FPGAs). Many machine learning frameworks include optimizations that leverage tensor decomposition to improve model execution speed and reduce energy consumption. Decomposing tensors into structured low-rank components aligns well with the memory hierarchy of modern hardware accelerators, facilitating more efficient data movement and parallel computation.

Despite these advantages, tensor decomposition introduces certain trade-offs that must be carefully managed. The choice of decomposition method and rank significantly influences model accuracy and computational efficiency. Selecting an overly aggressive rank reduction may lead to excessive information loss, while retaining too many components diminishes the efficiency gains. Additionally, the factorization process itself can introduce a computational overhead, requiring careful consideration when applying tensor decomposition to large-scale machine learning systems.

Trade-offs and Challenges

While tensor decomposition provides significant efficiency gains in machine learning systems, it introduces trade-offs that must be carefully managed to maintain model accuracy and computational feasibility. These trade-offs primarily involve the selection of decomposition rank, the computational complexity of factorization, and the stability of factorized representations.

One of the primary challenges in tensor decomposition is determining an appropriate rank for the factorized representation. In low-rank matrix factorization, the rank defines the dimensionality of the factorized matrices, directly influencing the balance between compression and information retention. In tensor decomposition, rank selection becomes even more complex, as different decomposition methods define rank in varying ways. For instance, in CANDECOMP/PARAFAC (CP) decomposition, the rank corresponds to the number of rank-one tensors used to approximate the original tensor. In Tucker decomposition, the rank is determined by the dimensions of the core tensor, while in Tensor-Train (TT) decomposition, the ranks of the factorized components dictate the level of compression. Selecting an insufficient rank can lead to excessive information loss, degrading the model’s predictive performance, whereas an overly conservative rank reduction results in limited compression benefits.

Another key challenge is the computational overhead associated with performing tensor decomposition. The factorization process itself requires solving an optimization problem, often involving iterative procedures such as alternating least squares (ALS) or stochastic gradient descent (SGD). These methods can be computationally expensive, particularly for large-scale tensors used in machine learning models. Additionally, during inference, the need to reconstruct tensors from their factorized components introduces additional matrix and tensor multiplications, which may increase computational latency. The efficiency of tensor decomposition in practice depends on striking a balance between reducing parameter storage and minimizing the additional computational cost incurred by factorized representations.

Numerical stability is another concern when applying tensor decomposition to machine learning models. Factorized representations can suffer from numerical instability, particularly when the original tensor contains highly correlated structures or when decomposition methods introduce ill-conditioned factors. Regularization techniques, such as adding constraints on factor matrices or applying low-rank approximations incrementally, can help mitigate these issues. Additionally, the optimization process used for decomposition must be carefully tuned to avoid convergence to suboptimal solutions that fail to preserve the essential properties of the original tensor.

Despite these challenges, tensor decomposition remains a valuable tool for optimizing machine learning models, particularly in applications where reducing memory footprint and computational complexity is a priority. Advances in adaptive decomposition methods, automated rank selection strategies, and hardware-aware factorization techniques continue to improve the practical utility of tensor decomposition in machine learning. The following section will summarize the key insights gained from low-rank matrix factorization and tensor decomposition, highlighting their role in designing efficient machine learning systems.

Comparison of LRMF and TD

Both low-rank matrix factorization (LRMF) and tensor decomposition serve as fundamental techniques for reducing the complexity of machine learning models by approximating large parameter structures with lower-rank representations. While they share the common goal of improving storage efficiency and computational performance, their applications, computational trade-offs, and structural assumptions differ significantly. This section provides a comparative analysis of these two techniques, highlighting their advantages, limitations, and practical use cases in machine learning systems.

One of the key distinctions between LRMF and tensor decomposition lies in the dimensionality of the data they operate on. LRMF applies to two-dimensional matrices, making it particularly useful for compressing weight matrices in fully connected layers or embeddings. Tensor decomposition, on the other hand, extends factorization to multi-dimensional tensors, which arise naturally in convolutional layers, attention mechanisms, and multi-modal learning. This generalization allows tensor decomposition to exploit additional structural properties of high-dimensional data that LRMF cannot capture.

Computationally, both methods introduce trade-offs between storage savings and inference speed. LRMF reduces the number of parameters in a model by factorizing a weight matrix into two smaller matrices, thereby reducing memory footprint while incurring an additional matrix multiplication during inference. In contrast, tensor decomposition further reduces storage by decomposing tensors into multiple lower-rank components, but at the cost of more complex tensor contractions, which may introduce higher computational overhead. The choice between these methods depends on whether the primary constraint is memory storage or inference latency.

@#tbl-lrmf-tensor summarizes the key differences between LRMF and tensor decomposition:

Table 10.5: Comparing LRMF with tensor decomposition.

Feature	Low-Rank Matrix Factorization (LRMF)	Tensor Decomposition
Applicable Data Structure	Two-dimensional matrices	Multi-dimensional tensors
Compression Mechanism	Factorizes a matrix into two or more lower-rank matrices	Decomposes a tensor into multiple lower-rank components
Common Methods	Singular Value Decomposition (SVD), Alternating Least Squares (ALS)	CP Decomposition, Tucker Decomposition, Tensor-Train (TT)
Computational Complexity	Generally lower, often $ O(mnk) $ for a rank-$ k $ approximation	Higher, due to iterative optimization and tensor contractions
Storage Reduction	Reduces storage from $ O(mn) $ to $ O(mk + kn) $	Achieves higher compression but requires more complex storage representations
Inference Overhead	Requires additional matrix multiplication	Introduces additional tensor operations, potentially increasing inference latency
Primary Use Cases	Fully connected layers, embeddings, recommendation systems	Convolutional filters, attention mechanisms, multi-modal learning
Implementation Complexity	Easier to implement, often involves direct factorization methods	More complex, requiring iterative optimization and rank selection

Despite these differences, LRMF and tensor decomposition are not mutually exclusive. In many machine learning models, both methods can be applied together to optimize different components of the architecture. For example, fully connected layers may be compressed using LRMF, while convolutional kernels and attention tensors undergo tensor decomposition. The choice of technique ultimately depends on the specific characteristics of the model and the trade-offs between storage efficiency and computational complexity.

10.4.4 Neural Architecture Search

The techniques discussed in previous sections—pruning, knowledge distillation, and many others—rely on human expertise to determine optimal model configurations. While these manual approaches have led to significant advancements, they are inherently slow, resource-intensive, and constrained by human biases. Selecting an optimal architecture requires extensive experimentation, and even experienced practitioners may overlook more efficient designs (Elsken, Metzen, and Hutter 2019a).

———. 2019a. “Neural Architecture Search.” In Automated Machine Learning, 20:63–77. 55. Springer International Publishing. https://doi.org/10.1007/978-3-030-05318-5\_3.

Zoph, Barret, and Quoc V Le. 2017a. “Neural Architecture Search with Reinforcement Learning.” In International Conference on Learning Representations (ICLR).

NAS addresses these limitations by automating model design. Instead of manually tuning configurations, NAS systematically explores a large space of architectures to identify those that best balance accuracy, computational cost, memory efficiency, and inference latency. By framing model selection as a structured search problem, NAS reduces reliance on trial and error, allowing architectures to be discovered programmatically rather than heuristically (Zoph and Le 2017a).

NAS formalizes model design as an optimization problem, leveraging techniques such as reinforcement learning, evolutionary algorithms, and gradient-based methods to automate decisions traditionally made by experts (Real et al. 2019a). This approach integrates principles of scaling optimization, structural pruning, and compressed representations, offering a unified framework for model efficiency.

———. 2019a. “Regularized Evolution for Image Classifier Architecture Search.” Proceedings of the AAAI Conference on Artificial Intelligence 33 (01): 4780–89. https://doi.org/10.1609/aaai.v33i01.33014780.

Real-world applications demonstrate that NAS-generated architectures often match or surpass human-designed models in efficiency and accuracy. Examples include models optimized for mobile and cloud environments, where inference latency and memory constraints are critical considerations. Ultimately, NAS encapsulates a holistic approach to model optimization, unifying multiple strategies into an automated, scalable framework.

Encoding Model Efficiency

NAS operates in three key stages: defining the search space, exploring candidate architectures, and evaluating their performance. The search space defines the architectural components and constraints that NAS can modify. The search strategy determines how NAS explores possible architectures, selecting promising candidates based on past observations. The evaluation process ensures that the discovered architectures satisfy multiple objectives, including accuracy, efficiency, and hardware suitability.

Search Space Definition: This stage establishes the architectural components and constraints NAS can modify, such as the number of layers, convolution types, activation functions, and hardware-specific optimizations. A well-defined search space balances innovation with computational feasibility.
Search Strategy: NAS explores the search space using methods such as reinforcement learning, evolutionary algorithms, or gradient-based techniques. These approaches guide the search toward architectures that maximize performance while meeting resource constraints.
Evaluation Criteria: Candidate architectures are assessed based on multiple metrics, including accuracy, FLOPs, memory consumption, inference latency, and power efficiency. NAS ensures that the selected architectures align with deployment requirements.

NAS unifies structural design and optimization into a singular, automated framework. The result is the discovery of architectures that are not only highly accurate but also computationally efficient and well-suited for target hardware platforms.

Defining the Search Space

The first step in NAS is determining the set of architectures it is allowed to explore, known as the search space. The size and structure of this space directly affect how efficiently NAS can discover optimal models. A well-defined search space must be broad enough to allow innovation while remaining narrow enough to prevent unnecessary computation on impractical designs.

A typical NAS search space consists of modular building blocks that define the structure of the model. These include the types of layers available for selection, such as standard convolutions, depthwise separable convolutions, attention mechanisms, and residual blocks. The search space also defines constraints on network depth and width, specifying how many layers the model can have and how many channels each layer should include. Additionally, NAS considers activation functions, such as ReLU, Swish, or GELU, which influence both model expressiveness and computational efficiency.

Other architectural decisions within the search space include kernel sizes, receptive fields, and skip connections, which impact both feature extraction and model complexity. Some NAS implementations also incorporate hardware-aware optimizations, ensuring that the discovered architectures align with specific hardware, such as GPUs, TPUs, or mobile CPUs.

The choice of search space determines the extent to which NAS can optimize a model. If the space is too constrained, the search algorithm may fail to discover novel and efficient architectures. If it is too large, the search becomes computationally expensive, requiring extensive resources to explore a vast number of possibilities. Striking the right balance ensures that NAS can efficiently identify architectures that improve upon human-designed models.

Exploring the Search Space

Once the search space is defined, NAS must decide how to explore different architectures to determine which designs are most effective. The search strategy guides this process, selecting which architectures to evaluate based on past observations. An effective search strategy must balance exploration—testing new architectures—and exploitation—refining promising designs.

Several methods have been developed to navigate the search space efficiently. Reinforcement learning-based NAS formulates the search process as a decision-making problem, where an agent sequentially selects architectural components and receives a reward signal based on the performance of the generated model. Over time, the agent learns to generate better architectures by maximizing this reward. While effective, reinforcement learning-based NAS can be computationally expensive because it requires training many candidate models before converging on an optimal design.

An alternative approach uses evolutionary algorithms, which maintain a population of candidate architectures and iteratively improve them through mutation and selection. Stronger architectures—those with higher accuracy and efficiency—are retained, while modifications such as changing layer types or filter sizes introduce new variations. This approach has been shown to balance exploration and computational feasibility more effectively than reinforcement learning-based NAS.

More recent methods, such as gradient-based NAS, introduce differentiable parameters that represent architectural choices. Instead of treating architectures as discrete entities, gradient-based methods optimize both model weights and architectural parameters simultaneously using standard gradient descent. This significantly reduces the computational cost of the search, making NAS more practical for real-world applications.

The choice of search strategy has a direct impact on the feasibility of NAS. Early NAS methods that relied on reinforcement learning required weeks of GPU computation to discover a single architecture. More recent methods, particularly those based on gradient-based search, have significantly reduced this cost, making NAS more efficient and accessible.

Evaluating the Candidate Architectures

Every architecture explored by NAS must be evaluated based on a set of predefined criteria. While accuracy is a fundamental metric, NAS also optimizes for efficiency constraints to ensure that models are practical for deployment. The evaluation process determines whether an architecture should be retained for further refinement or discarded in favor of more promising designs.

The primary evaluation metrics include computational complexity, memory consumption, inference latency, and energy efficiency. Computational complexity, often measured in FLOPs, determines the overall resource demands of a model. NAS favors architectures that achieve high accuracy while reducing unnecessary computations. Memory consumption, which includes both parameter count and activation storage, ensures that models fit within hardware constraints. For real-time applications, inference latency is a key factor, with NAS selecting architectures that minimize execution time on specific hardware platforms. Finally, some NAS implementations explicitly optimize for power consumption, ensuring that models are suitable for mobile and edge devices.

For example, FBNet, a NAS-generated architecture optimized for mobile inference, incorporated latency constraints into the search process. Instead of selecting the most accurate model, NAS identified architectures that provided the best balance between accuracy and inference speed (B. Wu et al. 2019). Similarly, EfficientNet was discovered through NAS by jointly optimizing for accuracy and computational efficiency, resulting in a model that delivers state-of-the-art performance while reducing FLOPs compared to conventional architectures (Tan and Le 2019a).

Wu, Bichen, Kurt Keutzer, Xiaoliang Dai, Peizhao Zhang, Yanghan Wang, Fei Sun, Yiming Wu, Yuandong Tian, Peter Vajda, and Yangqing Jia. 2019. “FBNet: Hardware-Aware Efficient ConvNet Design via Differentiable Neural Architecture Search.” In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 10726–34. IEEE. https://doi.org/10.1109/cvpr.2019.01099.

Tan, Mingxing, and Quoc V Le. 2019a. “EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks.” In International Conference on Machine Learning (ICML), 6105–14.

By integrating these constraints into the search process, NAS systematically discovers architectures that balance accuracy, efficiency, and hardware adaptability. Instead of manually fine-tuning these trade-offs, NAS automates the selection of optimal architectures, ensuring that models are well-suited for real-world deployment scenarios.

Examples of NAS-Discovered Architectures

NAS has been successfully used to design several state-of-the-art architectures that outperform manually designed models in terms of efficiency and accuracy. These architectures illustrate how NAS integrates scaling optimization, computation reduction, memory efficiency, and hardware-aware design into an automated process.

One of the most well-known NAS-generated models is EfficientNet, which was discovered using a NAS framework that searched for the most effective combination of depth, width, and resolution scaling. Unlike traditional scaling strategies that independently adjust these factors, NAS optimized the model using compound scaling, which applies a fixed set of scaling coefficients to ensure that the network grows in a balanced way. EfficientNet achieves higher accuracy with fewer parameters and lower FLOPs than previous architectures, making it ideal for both cloud and mobile deployment.

Another key example is MobileNetV3, which used NAS to optimize its network structure for mobile hardware. The search process led to the discovery of inverted residual blocks with squeeze-and-excitation layers, which improve accuracy while reducing computational cost. NAS also selected optimized activation functions and efficient depthwise separable convolutions, leading to a 5× reduction in FLOPs compared to earlier MobileNet versions.

FBNet, another NAS-generated model, was specifically optimized for real-time inference on mobile CPUs. Unlike architectures designed for general-purpose acceleration, FBNet’s search process explicitly considered latency constraints during training, ensuring that the final model runs efficiently on low-power hardware. Similar approaches have been used in TPU-optimized NAS models, where the search process is guided by hardware-aware cost functions to maximize parallel execution efficiency.

NAS has also been applied beyond convolutional networks. NAS-BERT explores transformer-based architectures, searching for efficient model structures that retain strong natural language understanding capabilities while reducing compute and memory overhead. NAS has been particularly useful in designing efficient vision transformers (ViTs) by automatically discovering lightweight attention mechanisms tailored for edge AI applications.

Each of these NAS-generated models demonstrates how automated architecture search can uncover novel efficiency trade-offs that may not be immediately intuitive to human designers. Explicit encoding of efficiency constraints into the search process enables NAS to systematically produce architectures that are more computationally efficient, memory-friendly, and hardware-adapted than those designed manually (Radosavovic et al. 2020).

Radosavovic, Ilija, Raj Prateek Kosaraju, Ross Girshick, Kaiming He, and Piotr Dollar. 2020. “Designing Network Design Spaces.” In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 10428–36. IEEE. https://doi.org/10.1109/cvpr42600.2020.01044.

10.5 Optimizing Numerical Precision

Machine learning models perform computations using numerical representations, and the choice of precision directly affects memory usage, computational efficiency, and power consumption. Many state-of-the-art models are trained and deployed using high-precision floating-point formats, such as FP32 (32-bit floating point), which offer numerical stability and high accuracy (Gupta et al. 2015). However, high-precision formats increase storage requirements, memory bandwidth usage, and power consumption, making them inefficient for large-scale or resource-constrained deployments.

Gupta, Suyog, Ankur Agrawal, Kailash Gopalakrishnan, and Pritish Narayanan. 2015. “Deep Learning with Limited Numerical Precision.” In International Conference on Machine Learning, 1737–46. PMLR.

Wang, Yu Emma, Gu-Yeon Wei, and David Brooks. 2019. “Benchmarking TPU, GPU, and CPU Platforms for Deep Learning.” arXiv Preprint arXiv:1907.10701.

Reducing numerical precision improves efficiency by reducing storage needs, decreasing data movement between memory and compute units, and enabling faster computation. Many modern AI accelerators, such as TPUs, GPUs, and edge AI chips, include dedicated hardware for low-precision computation, allowing FP16 and INT8 operations to run at significantly higher throughput than FP32 (Y. E. Wang, Wei, and Brooks 2019). However, reducing precision introduces quantization error, which can lead to accuracy degradation. The extent to which precision can be reduced depends on the model architecture, dataset properties, and hardware support.

This section explores the role of numerical precision in model efficiency, examining the trade-offs between different precision formats, methods for precision reduction, the benefits of custom and adaptive numerical representations, and extreme cases where models operate using only a few discrete numerical states (binarization and ternarization).

10.5.1 Numerical Precision for Efficiency

Efficient numerical representations enable significant reductions in storage requirements, computation latency, and power usage. By lowering precision, models can perform inference more efficiently, making this approach particularly beneficial for mobile AI, embedded systems, and cloud inference, where efficiency constraints are paramount. Moreover, efficient numerics facilitate hardware-software co-design, allowing precision levels to be tuned to specific hardware capabilities, thereby maximizing throughput on AI accelerators such as GPUs, TPUs, NPUs, and edge AI chips.

Energy Costs of Numerical Precision

The energy costs associated with different numerical precisions further highlight the benefits of reducing precision. As shown in Figure 10.12, performing a 32-bit floating-point addition (FAdd) consumes approximately 0.9 pJ, whereas a 16-bit floating-point addition only requires 0.4 pJ. Similarly, a 32-bit integer addition costs 0.1 pJ, while an 8-bit integer addition is significantly lower at just 0.03 pJ. These savings compound when considering large-scale models operating across billions of operations.

Beyond direct compute savings, reducing numerical precision has a significant impact on memory energy consumption, which often dominates total system power. Lower-precision representations reduce data storage requirements and memory bandwidth usage, leading to fewer and more efficient memory accesses. This is critical because accessing memory—especially off-chip DRAM—is far more energy-intensive than performing arithmetic operations. For instance, DRAM accesses require orders of magnitude more energy (1.3–2.6 nJ) compared to cache accesses (e.g., 10 pJ for an 8KB L1 cache access). The breakdown of instruction energy further underscores the cost of moving data within the memory hierarchy, where an instruction’s total energy can be significantly impacted by memory access patterns.

By reducing numerical precision, models can not only execute computations more efficiently but also reduce data movement, leading to lower overall energy consumption. This is particularly important for hardware accelerators and edge devices, where memory bandwidth and power efficiency are key constraints.

Performance Gains from Quantization

Figure 10.13 illustrates the impact of quantization on both inference time and model size using a stacked bar chart with a dual-axis representation. The left bars in each category show inference time improvements when moving from FP32 to INT8, while the right bars depict the corresponding reduction in model size. The results indicate that quantized models achieve up to 4× faster inference while reducing storage requirements by a factor of 4×, making them highly suitable for deployment in resource-constrained environments.

Figure 10.13: Impact of quantization on inference time and model size. The left stacked bars show inference time improvements, while the right stacked bars highlight memory savings.

However, reducing numerical precision introduces trade-offs. Lower-precision formats can lead to numerical instability and quantization noise, potentially affecting model accuracy. Some architectures, such as large transformer-based NLP models, tolerate precision reduction well, whereas others may experience significant degradation. Thus, selecting the appropriate numerical precision requires balancing accuracy constraints, hardware support, and efficiency gains.

Trade-offs in Numerical Precision Reduction

The figure above illustrates the quantization error weighted by the probability distribution of values, comparing different numerical formats (FP8 variants and INT8). The error distribution highlights how different formats introduce varying levels of quantization noise across the range of values, which in turn influences model accuracy and stability.

10.5.2 Numeric Encoding and Storage

The representation of numerical data in machine learning systems extends beyond precision levels to encompass encoding formats and storage mechanisms, both of which significantly influence computational efficiency. The encoding of numerical values determines how floating-point and integer representations are stored in memory and processed by hardware, directly affecting performance in machine learning workloads. As machine learning models grow in size and complexity, optimizing numeric encoding becomes increasingly critical for ensuring efficiency, particularly on specialized hardware accelerators (Mellempudi et al. 2019).

Mellempudi, Naveen, Sudarshan Srinivasan, Dipankar Das, and Bharat Kaul. 2019. “Mixed Precision Training with 8-Bit Floating Point.” arXiv Preprint arXiv:1905.12334.

Floating-point representations, which are widely used in machine learning, follow the IEEE 754 standard, defining how numbers are represented using a combination of sign, exponent, and mantissa (fraction) bits. Standard formats such as FP32 (single precision) and FP64 (double precision) provide high accuracy but demand substantial memory and computational resources. To enhance efficiency, reduced-precision formats such as FP16, bfloat16, and FP8 have been introduced, offering lower storage requirements while maintaining sufficient numerical range for machine learning computations. Unlike FP16, which allocates more bits to the mantissa, bfloat16 retains the same exponent size as FP32, allowing it to represent a wider dynamic range while reducing precision in the fraction. This characteristic makes bfloat16 particularly effective for machine learning training, where maintaining dynamic range is critical for stable gradient updates.

Integer-based representations, including INT8 and INT4, further reduce storage and computational overhead by eliminating the need for exponent and mantissa encoding. These formats are commonly used in quantized inference, where model weights and activations are converted to discrete integer values to accelerate computation and reduce power consumption. The deterministic nature of integer arithmetic simplifies execution on hardware, making it particularly well-suited for edge AI and mobile devices. At the extreme end, binary and ternary representations restrict values to just one or two bits, leading to significant reductions in memory footprint and power consumption. However, such aggressive quantization can degrade model accuracy unless complemented by specialized training techniques or architectural adaptations.

Emerging numeric formats seek to balance the trade-off between efficiency and accuracy. TF32, introduced by NVIDIA for Ampere GPUs, modifies FP32 by reducing the mantissa size while maintaining the exponent width, allowing for faster computations with minimal precision loss. Similarly, FP8, gaining adoption in AI accelerators, provides an even lower-precision floating-point alternative while retaining a structure that aligns well with machine learning workloads (Micikevicius et al. 2022). Alternative formats such as Posit, Flexpoint, and BF16ALT are also being explored for their potential advantages in numerical stability and hardware adaptability.

Micikevicius, Paulius, Dusan Stosic, Neil Burgess, Marius Cornea, Pradeep Dubey, Richard Grisenthwaite, Sangwon Ha, et al. 2022. “FP8 Formats for Deep Learning.” arXiv Preprint arXiv:2209.05433. https://arxiv.org/abs/2209.05433.

The efficiency of numeric encoding is further influenced by how data is stored and accessed in memory. AI accelerators optimize memory hierarchies to maximize the benefits of reduced-precision formats, leveraging specialized hardware such as tensor cores, matrix multiply units (MMUs), and vector processing engines to accelerate lower-precision computations. On these platforms, data alignment, memory tiling, and compression techniques play a crucial role in ensuring that reduced-precision computations deliver tangible performance gains.

As machine learning systems evolve, numeric encoding and storage strategies will continue to adapt to meet the demands of large-scale models and diverse hardware environments. The ongoing development of precision formats tailored for AI workloads highlights the importance of co-designing numerical representations with underlying hardware capabilities, ensuring that machine learning models achieve optimal performance while minimizing computational costs.

10.5.3 Comparison of Numerical Precision Formats

Table 11.5 compares commonly used numerical precision formats in machine learning, highlighting their trade-offs in storage efficiency, computational speed, and energy consumption. Emerging formats like FP8 and TF32 have been introduced to further optimize performance, particularly on AI accelerators.

Table 10.6: Comparison of numerical precision formats.

Precision Format	Bit-Width	Storage Reduction (vs FP32)	Compute Speed (vs FP32)	Power Consumption	Use Cases
FP32 (Single-Precision Floating Point)	32-bit	Baseline (1×)	Baseline (1×)	High	Training & inference (general-purpose)
FP16 (Half-Precision Floating Point)	16-bit	2× smaller	2× faster on FP16-optimized hardware	Lower	Accelerated training, inference (NVIDIA Tensor Cores, TPUs)
bfloat16 (Brain Floating Point)	16-bit	2× smaller	Similar speed to FP16, better dynamic range	Lower	Training on TPUs, transformer-based models
TF32 (TensorFloat-32)	19-bit	Similar to FP16	Up to 8× faster on NVIDIA Ampere GPUs	Lower	Training on NVIDIA GPUs
FP8 (Floating-Point 8-bit)	8-bit	4× smaller	Faster than INT8 in some cases	Significantly lower	Efficient training/inference (H100, AI accelerators)
INT8 (8-bit Integer)	8-bit	4× smaller	4–8× faster than FP32	Significantly lower	Quantized inference (Edge AI, mobile AI, NPUs)
INT4 (4-bit Integer)	4-bit	8× smaller	Hardware-dependent	Extremely low	Ultra-low-power AI, experimental quantization
Binary/Ternary (1-bit / 2-bit)	1–2-bit	16–32× smaller	Highly hardware-dependent	Lowest	Extreme efficiency (binary/ternary neural networks)

FP16 and bfloat16 formats provide moderate efficiency gains while preserving model accuracy. Many AI accelerators, such as NVIDIA Tensor Cores and TPUs, include dedicated support for FP16 computations, enabling 2× faster matrix operations compared to FP32. BFloat16, in particular, retains the same 8-bit exponent as FP32 but with a reduced 7-bit mantissa, allowing it to maintain a similar dynamic range (~$10^{-38}$ to $10^{38}$) while sacrificing precision. In contrast, FP16, with its 5-bit exponent and 10-bit mantissa, has a significantly reduced dynamic range (~$10^{-5}$ to $10^5$), making it more suitable for inference rather than training. Since BFloat16 preserves the exponent size of FP32, it better handles extreme values encountered during training, whereas FP16 may struggle with underflow or overflow. This makes BFloat16 a more robust alternative for deep learning workloads that require a wide dynamic range.

Figure 10.14 highlights these differences, showing how bit-width allocations impact the trade-offs between precision and numerical range.

Figure 10.14: Three floating-point formats.

INT8 precision offers more aggressive efficiency improvements, particularly for inference workloads. Many quantized models use INT8 for inference, reducing storage by 4× while accelerating computation by 4–8× on optimized hardware. INT8 is widely used in mobile and embedded AI, where energy constraints are significant.

Binary and ternary networks represent the extreme end of precision reduction, where weights and activations are constrained to 1-bit (binary) or 2-bit (ternary) values. This results in massive storage and energy savings, but model accuracy often degrades significantly unless specialized architectures are used.

10.5.4 Trade-offs in Precision Reduction

Reducing numerical precision in machine learning systems offers substantial gains in efficiency, including lower memory requirements, reduced power consumption, and increased computational throughput. However, these benefits come with trade-offs, as lower-precision representations introduce numerical error and quantization noise, which can affect model accuracy. The extent of this impact depends on multiple factors, including the model architecture, the dataset, and the specific precision format used.

Models exhibit varying levels of tolerance to precision reduction. Large-scale architectures, such as convolutional neural networks and transformer-based models, often retain high accuracy even when using reduced-precision formats such as bfloat16 or INT8. In contrast, smaller models or those trained on tasks requiring high numerical precision may experience greater degradation in performance. Additionally, not all layers within a neural network respond equally to precision reduction. Certain layers, such as batch normalization and attention mechanisms, may be more sensitive to numerical precision than standard feedforward layers. As a result, techniques such as mixed-precision training, where different layers operate at different levels of precision, can help maintain accuracy while optimizing computational efficiency.

Hardware support is another critical factor in determining the effectiveness of precision reduction. AI accelerators, including GPUs, TPUs, and NPUs, are designed with dedicated low-precision arithmetic units that enable efficient computation using FP16, bfloat16, INT8, and, more recently, FP8. These architectures exploit reduced precision to perform high-throughput matrix operations, improving both speed and energy efficiency. In contrast, general-purpose CPUs often lack specialized hardware for low-precision computations, limiting the potential benefits of numerical precision reduction. The introduction of newer floating-point formats, such as TF32 for NVIDIA GPUs and FP8 for AI accelerators, seeks to optimize the trade-off between precision and efficiency, offering an alternative for hardware that is not explicitly designed for extreme quantization.

In addition to hardware constraints, reducing numerical precision impacts power consumption. Lower-precision arithmetic reduces the number of required memory accesses and simplifies computational operations, leading to lower overall energy use. This is particularly advantageous for energy-constrained environments such as mobile devices and edge AI systems. At the extreme end, ultra-low precision formats, including INT4 and binary/ternary representations, provide substantial reductions in power and memory usage. However, these formats often require specialized architectures to compensate for the accuracy loss associated with such aggressive quantization.

To mitigate accuracy loss associated with reduced precision, various precision reduction strategies can be employed. Ultimately, selecting the appropriate numerical precision for a given machine learning model requires balancing efficiency gains against accuracy constraints. This selection depends on the model’s architecture, the computational requirements of the target application, and the underlying hardware’s support for low-precision operations. By leveraging advancements in both hardware and software optimization techniques, practitioners can effectively integrate lower-precision numerics into machine learning pipelines, maximizing efficiency while maintaining performance.

10.5.5 Precision Reduction Strategies

Reducing numerical precision is an essential optimization technique for improving the efficiency of machine learning models. By lowering the bit-width of weights and activations, models can reduce memory footprint, improve computational throughput, and decrease power consumption. However, naive precision reduction can introduce quantization errors, leading to accuracy degradation. To address this, different precision reduction strategies have been developed, allowing models to balance efficiency gains while preserving predictive performance.

Precision reduction techniques can be applied at different stages of a model’s lifecycle. Post-training quantization reduces precision after training, making it a simple and low-cost approach for optimizing inference. Quantization-aware training incorporates quantization effects into the training process, enabling models to adapt to lower precision and retain higher accuracy. Mixed-precision training leverages hardware support to dynamically assign precision levels to different computations, optimizing execution efficiency without sacrificing accuracy.

Post-Training Quantization

Post-training quantization (PTQ) is a widely used technique for optimizing machine learning models by reducing numerical precision after training, improving inference efficiency without requiring additional retraining (Jacob et al. 2018a). By converting model weights and activations from high-precision floating-point formats (e.g., FP32) to lower-precision representations (e.g., INT8 or FP16), PTQ enables smaller model sizes, faster computation, and reduced energy consumption. This makes it a practical choice for deploying models on resource-constrained environments, such as mobile devices, edge AI systems, and cloud inference platforms (H. Wu et al. 2020).

Unlike other quantization techniques that modify the training process, PTQ is applied after training is complete. This means that the model retains its original structure and parameters, but its numerical representation is changed to operate in a more efficient format. The key advantage of PTQ is its low computational cost, as it does not require retraining the model with quantization constraints. However, reducing precision can introduce quantization error, which may lead to accuracy degradation, especially in tasks that rely on fine-grained numerical precision.

PTQ is widely supported in machine learning frameworks such as TensorFlow Lite, ONNX Runtime, and PyTorch’s quantization toolkit, making it an accessible and practical approach for optimizing inference workloads. The following sections explore how PTQ works, its benefits and challenges, and techniques for mitigating accuracy loss.

How PTQ Works

PTQ converts a trained model’s weights and activations from high-precision floating-point representations (e.g., FP32) to lower-precision formats (e.g., INT8 or FP16). This process reduces the memory footprint of the model, accelerates inference, and lowers power consumption. However, since lower-precision formats have a smaller numerical range, quantization introduces rounding errors, which can impact model accuracy.

The core mechanism behind PTQ is scaling and mapping high-precision values into a reduced numerical range. A widely used approach is uniform quantization, which maps floating-point values to discrete integer levels using a consistent scaling factor. In uniform quantization, the interval between each quantized value is constant, simplifying implementation and ensuring efficient execution on hardware. The quantized value $q$ is computed as:

\[ q = \text{round} \left(\frac{x}{s} \right) \]

where:

$q$ is the quantized integer representation,
$x$ is the original floating-point value,
$s$ is a scaling factor that maps the floating-point range to the available integer range.

For example, in INT8 quantization, the model’s floating-point values (typically ranging from $[-r, r]$) are mapped to an integer range of $[-128, 127]$. The scaling factor ensures that the most significant information is retained while reducing precision loss. Once the model has been quantized, inference is performed using integer arithmetic, which is significantly more efficient than floating-point operations on many hardware platforms (Gholami et al. 2021a). However, due to rounding errors and numerical approximation, quantized models may experience slight accuracy degradation compared to their full-precision counterparts.

Once the model has been quantized, inference is performed using integer arithmetic, which is significantly more efficient than floating-point operations on many hardware platforms. However, due to rounding errors and numerical approximation, quantized models may experience slight accuracy degradation compared to their full-precision counterparts.

In addition to uniform quantization, non-uniform quantization can be employed to preserve accuracy in certain scenarios. Unlike uniform quantization, which uses a consistent scaling factor, non-uniform quantization assigns finer-grained precision to numerical ranges that are more densely populated. This approach can be beneficial for models with weight distributions that concentrate around certain values, as it allows more details to be retained where it matters most. However, non-uniform quantization typically requires more complex calibration and may involve additional computational overhead. While it is not as commonly used as uniform quantization in production environments, non-uniform techniques can be effective for preserving accuracy in models that are particularly sensitive to precision changes.

PTQ is particularly effective for computer vision models, where CNNs often tolerate quantization well. However, models that rely on small numerical differences, such as NLP transformers or speech recognition models, may require additional tuning or alternative quantization techniques, including non-uniform strategies, to retain performance.

Calibration

An important aspect of PTQ is the calibration step, which involves selecting the most effective clipping range [$\alpha$, $\beta$] for quantizing model weights and activations. During PTQ, the model’s weights and activations are converted to lower-precision formats (e.g., INT8), but the effectiveness of this reduction depends heavily on the chosen quantization range. Without proper calibration, the quantization process may cause significant accuracy degradation, even if the overall precision is reduced. Calibration ensures that the chosen range minimizes loss of information and helps preserve the model’s performance after precision reduction.

The overall workflow of post-training quantization is illustrated in Figure 10.15. The process begins with a pre-trained model, which serves as the starting point for optimization. To determine an effective quantization range, a calibration dataset, which is a representative subset of training or validation data—is passed through the model. This step allows the calibration process to estimate the numerical distribution of activations and weights, which is then used to define the clipping range for quantization. Following calibration, the quantization step converts the model parameters to a lower-precision format, producing the final quantized model, which is more efficient in terms of memory and computation.

Figure 10.15: Post-Training Quantization Workflow. Calibration uses a pre-trained model and calibration data to determine quantization ranges before applying precision reduction.

For example, consider quantizing activations that originally have a floating-point range between -6 and 6 to 8-bit integers. Simply using the full integer range of -128 to 127 for quantization might not be the most effective approach. Instead, calibration involves passing a representative dataset through the model and observing the actual range of the activations. The observed range can then be used to set a more effective quantization range, reducing information loss.

Methods

There are several commonly used calibration methods:

Max: This method uses the maximum absolute value seen during calibration as the clipping range. While simple, it is susceptible to outlier data. For example, in the activation distribution shown in Figure 10.16, we see an outlier cluster around 2.1, while the rest of the values are clustered around smaller values. The Max method could lead to an inefficient range if the outliers significantly influence the quantization.
Entropy: This method minimizes information loss between the original floating-point values and the values that could be represented by the quantized format, typically using KL divergence. This is the default calibration method used by TensorRT and works well when trying to preserve the distribution of the original values.
Percentile: This method sets the clipping range to a percentile of the distribution of absolute values seen during calibration. For example, a 99% calibration would clip the top 1% of the largest magnitude values. This method helps avoid the impact of outliers, which are not representative of the general data distribution.

Figure 10.16: Input activations to layer 3 in ResNet50. Source: @H. Wu et al. (2020).

The quality of calibration directly affects the performance of the quantized model. A poor calibration could lead to a model that suffers from significant accuracy loss, while a well-calibrated model can retain much of its original performance after quantization. Importantly, there are two types of calibration ranges to consider:

Symmetric Calibration: The clipping range is symmetric around zero, meaning both the positive and negative ranges are equally scaled.
Asymmetric Calibration: The clipping range is not symmetric, which means the positive and negative ranges may have different scaling factors. This can be useful when the data is not centered around zero.

Choosing the right calibration method and range is critical for maintaining model accuracy while benefiting from the efficiency gains of reduced precision.

Ranges

A key challenge in post-training quantization (PTQ) is selecting the appropriate calibration range $[$ , $]$ to map floating-point values into a lower-precision representation. The choice of this range directly affects the quantization error and, consequently, the accuracy of the quantized model. The figure below illustrates two different calibration strategies: symmetric calibration and asymmetric calibration.

Figure 10.17: Comparison of symmetric and asymmetric calibration methods.

On the left side of the figure, we see an example of symmetric calibration, where the clipping range is centered around zero. The range extends from $\alpha = -1$ to $\beta = 1$, mapping these values to the integer range of $[-127, 127]$. The symmetric mapping ensures that positive and negative values are treated equally, preserving zero-centered distributions. This approach simplifies implementation, as the same scale factor is applied to both positive and negative values. However, it may not be optimal for datasets where the activation distributions are skewed, as significant portions of the data may be poorly represented.

On the right side, we see an example of asymmetric calibration, where $\alpha = -0.5$ and $\beta = 1.5$. This results in a mapping where zero is shifted to a different quantized value $-Z$, and the range extends asymmetrically. In this case, the quantization scale is adjusted to account for the fact that the distribution of values is not symmetric around zero. Asymmetric calibration is particularly useful when activations or weights have a non-zero mean since it allows for a better fit to the observed data distribution. However, it requires additional computation to determine the optimal offset and scaling factors.

Symmetric calibration is commonly used when weight distributions are centered around zero, which is often the case for well-initialized machine learning models. It simplifies computation and hardware implementation but may not be optimal for all scenarios.
Asymmetric calibration is useful when the data distribution is skewed, ensuring that the full quantized range is effectively utilized. It can improve accuracy retention but may introduce additional computational complexity in determining the optimal quantization parameters.

The choice between these calibration strategies depends on the specific model and dataset. In practice, many machine learning frameworks, such as TensorRT and PyTorch, support both symmetric and asymmetric calibration modes, allowing developers to experiment and choose the best approach based on empirical results.

Selecting an appropriate calibration range can help PTQ better preserve model accuracy while still achieving the efficiency benefits of reduced numerical precision.

Granularity

After determining the clipping range, the next step in optimizing quantization involves adjusting the granularity of the clipping range to ensure that the model retains as much accuracy as possible. In CNNs, for instance, the input activations of a layer undergo convolution with multiple convolutional filters, each of which may have a unique range of values. The quantization process, therefore, must account for these differences in range across filters to preserve the model’s performance.

As illustrated in Figure 10.18, the range for Filter 1 is significantly smaller than that for Filter 3, demonstrating the variation in the magnitude of values across different filters. The precision with which the clipping range [$\alpha$, $\beta$] is determined for the weights becomes a critical factor in effective quantization. This variability in ranges is a key reason why different quantization strategies, based on granularity, are employed.

Figure 10.18: Quantization granularity: variable ranges. Source: Gholami et al. (2021a).

Several methods are commonly used to determine the granularity of quantization, each with its own trade-offs in terms of accuracy, efficiency, and computational cost.

Layerwise Quantization

In this approach, the clipping range is determined by considering all weights in the convolutional filters of a layer. The same clipping range is applied to all filters within the layer. While this method is simple to implement, it often leads to suboptimal accuracy due to the wide range of values across different filters. For example, if one convolutional kernel has a narrower range of values than another in the same layer, the quantization resolution of the narrower range may be compromised, resulting in a loss of information.

Groupwise Quantization

Groupwise quantization divides the convolutional filters into groups and calculates a shared clipping range for each group. This method can be beneficial when the distribution of values within a layer is highly variable. For example, the Q-BERT model (Shen et al. 2019) applied this technique when quantizing Transformer models (Chen et al. 2018), particularly for the fully-connected attention layers. While groupwise quantization offers better accuracy than layerwise quantization, it incurs additional computational cost due to the need to account for multiple scaling factors.

Shen, Sheng, Zhen Dong, Jiayu Ye, Linjian Ma, Zhewei Yao, Amir Gholami, Michael W. Mahoney, and Kurt Keutzer. 2019. “Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT.” Proceedings of the AAAI Conference on Artificial Intelligence 34 (05): 8815–21. https://doi.org/10.1609/aaai.v34i05.6409.

Chen, Mia Xu, Orhan Firat, Ankur Bapna, Melvin Johnson, Wolfgang Macherey, George Foster, Llion Jones, et al. 2018. “The Best of Both Worlds: Combining Recent Advances in Neural Machine Translation.” In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), 30:5998–6008. Association for Computational Linguistics. https://doi.org/10.18653/v1/p18-1008.

Channelwise Quantization

Channelwise quantization assigns a dedicated clipping range and scaling factor to each convolutional filter. This approach ensures a higher resolution in quantization, as each channel is quantized independently. Channelwise quantization is widely used in practice, as it often yields better accuracy compared to the previous methods. By allowing each filter to have its own clipping range, this method ensures that the quantization process is tailored to the specific characteristics of each filter.

Sub-channelwise Quantization

This method takes the concept of channelwise quantization a step further by subdividing each convolutional filter into smaller groups, each with its own clipping range. Although this method can provide very fine-grained control over quantization, it introduces significant computational overhead as multiple scaling factors must be managed for each group within a filter. As a result, sub-channelwise quantization is generally only used in scenarios where maximum precision is required, despite the increased computational cost.

Among these methods, channelwise quantization is the current standard for quantizing convolutional filters. It strikes a balance between the accuracy gains from finer granularity and the computational efficiency needed for practical deployment. Adjusting the clipping range for each individual kernel provides significant improvements in model accuracy with minimal overhead, making it the most widely adopted approach in machine learning applications.

Weights vs. Activations

Weight Quantization involves converting the continuous, high-precision weights of a model into lower-precision values, such as converting 32-bit floating-point (Float32) weights to 8-bit integer (INT8) weights. As illustrated in Figure 10.19, weight quantization occurs in the second step (red squares) during the multiplication of inputs. This process significantly reduces the model size, decreasing both the memory required to store the model and the computational resources needed for inference. For example, a weight matrix in a neural network layer with Float32 weights like [0.215, -1.432, 0.902, …] might be mapped to INT8 values such as [27, -183, 115, …], leading to a substantial reduction in memory usage.

Figure 10.19: Weight and activation quantization. Source: HarvardX.

Activation Quantization refers to the process of quantizing the activation values, or outputs of the layers, during model inference. This quantization can reduce the computational resources required during inference, particularly when targeting hardware optimized for integer arithmetic. It introduces challenges related to maintaining model accuracy, as the precision of intermediate computations is reduced. For instance, in a CNN, the activation maps (or feature maps) produced by convolutional layers, originally represented in Float32, may be quantized to INT8 during inference. This can significantly accelerate computation on hardware capable of efficiently processing lower-precision integers.

Recent advancements have explored Activation-aware Weight Quantization (AWQ) for the compression and acceleration of large language models (LLMs). This approach focuses on protecting only a small fraction of the most salient weights, approximately 1%, by observing the activations rather than the weights themselves. This method has been shown to improve model efficiency while preserving accuracy, as discussed in (Ji Lin et al. 2023).

Lin, Ji, Jiaming Tang, Haotian Tang, Shang Yang, Wei-Ming Chen, Wei-Chen Wang, Guangxuan Xiao, Xingyu Dang, Chuang Gan, and Song Han. 2023. “AWQ: Activation-Aware Weight Quantization for LLM Compression and Acceleration.” arXiv Preprint arXiv:2306.00978 abs/2306.00978 (June). http://arxiv.org/abs/2306.00978v5.

Static and Dynamic Quantization

After determining the type and granularity of the clipping range, practitioners must decide when the clipping ranges are calculated in their quantization algorithms. Two primary approaches exist for quantizing activations: static quantization and dynamic quantization.

Static Quantization is the more commonly used approach. In static quantization, the clipping range is pre-calculated and remains fixed during inference. This method does not introduce any additional computational overhead during runtime, which makes it efficient in terms of computational resources. However, the fixed range can lead to lower accuracy compared to dynamic quantization. A typical implementation of static quantization involves running a series of calibration inputs to compute the typical range of activations, as discussed in works like (Jacob et al. 2018a) and (Yao et al. 2021).

Yao, Zhewei, Amir Gholami, Sheng Shen, Kurt Keutzer, and Michael W. Mahoney. 2021. “HAWQ-V3: Dyadic Neural Network Quantization.” In Proceedings of the 38th International Conference on Machine Learning (ICML), 11875–86. PMLR.

In contrast, Dynamic Quantization dynamically calculates the range for each activation map during runtime. This approach allows the quantization process to adjust in real time based on the input, potentially yielding higher accuracy since the range is specifically calculated for each input activation. However, dynamic quantization incurs higher computational overhead because the range must be recalculated at each step. Although this often results in higher accuracy, the real-time computations can be expensive, particularly when deployed at scale.

The following table, Table 10.7, summarizes the characteristics of post-training quantization, quantization-aware training, and dynamic quantization, providing an overview of their respective strengths, limitations, and trade-offs. These methods are widely deployed across machine learning systems of varying scales, and understanding their pros and cons is crucial for selecting the appropriate approach for a given application.

Table 10.7: Comparison of post-training quantization, quantization-aware training, and dynamic quantization.

Aspect	Post Training Quantization	Quantization-Aware Training	Dynamic Quantization
Pros
Simplicity	✓	✗	✗
Accuracy Preservation	✗	✓	✓
Adaptability	✗	✗	✓
Optimized Performance	✗	✓	Potentially
Cons
Accuracy Degradation	✓	✗	Potentially
Computational Overhead	✗	✓	✓
Implementation Complexity	✗	✓	✓
Tradeoffs
Speed vs. Accuracy	✓	✗	✗
Accuracy vs. Cost	✗	✓	✗
Adaptability vs. Overhead	✗	✗	✓

Advantages of PTQ

One of the key advantages of PTQ is its low computational cost, as it does not require retraining the model. This makes it an attractive option for the rapid deployment of trained models, particularly when retraining is computationally expensive or infeasible. Since PTQ only modifies the numerical representation of weights and activations, the underlying model architecture remains unchanged, allowing it to be applied to a wide range of pre-trained models without modification.

PTQ also provides substantial memory and storage savings by reducing the bit-width of model parameters. For instance, converting a model from FP32 to INT8 results in a 4× reduction in storage size, making it feasible to deploy larger models on resource-constrained devices such as mobile phones, edge AI hardware, and embedded systems. These reductions in memory footprint also lead to lower bandwidth requirements when transferring models across networked systems.

In terms of computational efficiency, PTQ allows inference to be performed using integer arithmetic, which is inherently faster than floating-point operations on many hardware platforms. AI accelerators such as Tensor Processing Units (TPUs) and Neural Processing Units (NPUs) are optimized for lower-precision computations, enabling higher throughput and reduced power consumption when executing quantized models. This makes PTQ particularly useful for applications requiring real-time inference, such as object detection in autonomous systems or speech recognition on mobile devices.

Challenges and Limitations of PTQ

Despite its advantages, PTQ introduces quantization errors due to rounding effects when mapping floating-point values to discrete lower-precision representations. While some models remain robust to these changes, others may experience notable accuracy degradation, especially in tasks that rely on small numerical differences.

The extent of accuracy loss depends on both the model architecture and the task domain. CNNs for image classification are generally tolerant to PTQ, often maintaining near-original accuracy even with aggressive INT8 quantization. Transformer-based models used in natural language processing (NLP) and speech recognition tend to be more sensitive, as these architectures rely on the precision of numerical relationships in attention mechanisms.

To mitigate accuracy loss, calibration techniques such as KL divergence-based scaling or per-channel quantization are commonly applied to fine-tune the scaling factor and minimize information loss. Some frameworks, including TensorFlow Lite and PyTorch, provide automated quantization tools with built-in calibration methods to improve accuracy retention.

Another limitation of PTQ is that not all hardware supports efficient integer arithmetic. While GPUs, TPUs, and specialized edge AI chips often include dedicated support for INT8 inference, general-purpose CPUs may lack the optimized instructions for low-precision execution, resulting in suboptimal performance improvements.

Additionally, PTQ is not always suitable for training purposes. Since PTQ applies quantization after training, models that require further fine-tuning or adaptation may benefit more from alternative approaches, such as quantization-aware training (which we will discuss next), to ensure that precision constraints are adequately considered during the learning process.

Post-training quantization remains one of the most practical and widely used techniques for improving inference efficiency. It provides substantial memory and computational savings with minimal overhead, making it an ideal choice for deploying machine learning models in resource-constrained environments. However, the success of PTQ depends on model architecture, task sensitivity, and hardware compatibility. In scenarios where accuracy degradation is unacceptable, alternative quantization strategies, such as quantization-aware training, may be required.

Quantization-Aware Training

While PTQ offers a fast, computationally inexpensive approach for optimizing inference efficiency, it has inherent limitations; applying quantization after training does not consider the impacts of reduced numerical precision on model behavior. This oversight can result in noticeable accuracy degradation, particularly for models that rely on fine-grained numerical precision, such as transformers used in NLP and speech recognition systems (Nagel et al. 2021a).

———. 2021a. “A White Paper on Neural Network Quantization.” arXiv Preprint arXiv:2106.08295, June. http://arxiv.org/abs/2106.08295v1.

———. 2018a. “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference.” In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2704–13. IEEE. https://doi.org/10.1109/cvpr.2018.00286.

QAT addresses this limitation by integrating quantization constraints directly into the training process. Instead of reducing precision after training, QAT simulates low-precision arithmetic during forward passes, allowing the model to learn how to be more robust to quantization effects. This ensures that the model’s accuracy is better maintained once deployed with low-precision computations (Jacob et al. 2018a).

As illustrated in Figure Figure 10.20, QAT involves first applying quantization to a pre-trained model, followed by retraining or fine-tuning using training data. This process allows the model to adapt to low-precision numerical constraints, mitigating accuracy degradation.

Figure 10.20: Quantization-aware training process.

In many cases, QAT can also build off PTQ, as shown in Figure Figure 10.21. Instead of starting from a full-precision model, PTQ is first applied to produce an initial quantized model, leveraging calibration data to determine appropriate quantization parameters. This PTQ model then serves as the starting point for QAT, where additional fine-tuning with training data helps the model better adapt to low-precision constraints. This hybrid approach benefits from the efficiency of PTQ while reducing the accuracy degradation typically associated with post-training quantization alone.

Figure 10.21: Quantization-aware training process after PTQ.

Mathematical Formulation

During forward propagation, weights and activations are quantized and dequantized to mimic reduced precision. This process is typically represented as:

\[ q = \text{round} \left(\frac{x}{s} \right) \times s \]

where q represents the simulated quantized value, x denotes the full-precision weight or activation, and s is the scaling factor mapping floating-point values to lower-precision integers.

Although the forward pass utilizes quantized values, gradient calculations during backpropagation remain in full precision. This is achieved using the Straight-Through Estimator (STE), which approximates the gradient of the quantized function by treating the rounding operation as if it had a derivative of one. This approach prevents the gradient from being obstructed due to the non-differentiable nature of the quantization operation, thereby allowing effective model training (Y. Bengio, Léonard, and Courville 2013a).

———. 2013a. “Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation.” arXiv Preprint arXiv:1308.3432, August. http://arxiv.org/abs/1308.3432v1.

Krishnamoorthi, Raghuraman. 2018. “Quantizing Deep Convolutional Networks for Efficient Inference: A Whitepaper.” arXiv Preprint arXiv:1806.08342 abs/1806.08342 (June). http://arxiv.org/abs/1806.08342v1.

Integrating quantization effects during training enables the model to learn an optimal distribution of weights and activations that minimizes the impact of numerical precision loss. The resulting model, when deployed using true low-precision arithmetic (e.g., INT8 inference), maintains significantly higher accuracy than one that is quantized post hoc (Krishnamoorthi 2018).

Advantages of QAT

A primary advantage of QAT is its ability to maintain model accuracy, even under low-precision inference conditions. Incorporating quantization during training helps the model to compensate for precision loss, reducing the impact of rounding errors and numerical instability. This is critical for quantization-sensitive models commonly used in NLP, speech recognition, and high-resolution computer vision (Gholami et al. 2021a).

———. 2021a. “A Survey of Quantization Methods for Efficient Neural Network Inference.” arXiv Preprint arXiv:2103.13630 abs/2103.13630 (March). http://arxiv.org/abs/2103.13630v3.

Wu, Hao, Patrick Judd, Xiaojie Zhang, Mikhail Isaev, and Paulius Micikevicius. 2020. “Integer Quantization for Deep Learning Inference: Principles and Empirical Evaluation.” arXiv Preprint arXiv:2004.09602 abs/2004.09602 (April). http://arxiv.org/abs/2004.09602v1.

Another major benefit is that QAT permits low-precision inference on hardware accelerators without significant accuracy degradation. AI processors such as TPUs, NPUs, and specialized edge devices include dedicated hardware for integer operations, permitting INT8 models to run much faster and with lower energy consumption compared to FP32 models. Training with quantization effects in mind ensures that the final model can fully leverage these hardware optimizations (H. Wu et al. 2020).

Challenges and Trade-offs

Despite its benefits, QAT introduces additional computational overhead during training. Simulated quantization at every forward pass slows down training relative to full-precision methods. The process adds complexity to the training schedule, making QAT less practical for very large-scale models where the additional training time might be prohibitive.

Moreover, QAT introduces extra hyperparameters and design considerations, such as choosing appropriate quantization schemes and scaling factors. Unlike PTQ, which applies quantization after training, QAT requires careful tuning of the training dynamics to ensure that the model suitably adapts to low-precision constraints (Gong et al. 2019).

Gong, Ruihao, Xianglong Liu, Shenghu Jiang, Tianxiang Li, Peng Hu, Jiazhen Lin, Fengwei Yu, and Junjie Yan. 2019. “Differentiable Soft Quantization: Bridging Full-Precision and Low-Bit Neural Networks.” arXiv Preprint arXiv:1908.05033, August. http://arxiv.org/abs/1908.05033v1.

Table 10.8 summarizes the key trade-offs of QAT compared to PTQ:

Table 10.8: Comparison of QAT and PTQ.

Aspect	QAT (Quantization-Aware Training)	PTQ (Post-Training Quantization)
Accuracy Retention	Minimizes accuracy loss from quantization	May suffer from accuracy degradation
Inference Efficiency	Optimized for low-precision hardware (e.g., INT8 on TPUs)	Optimized but may require calibration
Training Complexity	Requires retraining with quantization constraints	No retraining required
Training Time	Slower due to simulated quantization in forward pass	Faster, as quantization is applied post hoc
Deployment Readiness	Best for models sensitive to quantization errors	Fastest way to optimize models for inference

Integrating quantization into the training process preserves model accuracy more effectively than post-training quantization, although it requires additional training resources and time.

PTQ and QAT Implementation Strategies

PTQ and QAT are supported across modern machine learning frameworks, facilitating efficient deployment of machine learning models on low-precision hardware. Although PTQ is simpler to implement since it does not require retraining, QAT embeds quantization into the training pipeline, leading to better accuracy retention. Each framework offers specialized tools that allow these methods to be applied effectively while balancing computational trade-offs.

TensorFlow implements PTQ using tf.lite.TFLiteConverter, which converts model weights and activations to lower-precision formats (e.g., INT8) post-training. Since PTQ circumvents retraining, calibration techniques such as per-channel quantization and KL-divergence scaling can be applied to minimize accuracy loss. TensorFlow also supports QAT through tf.keras.quantization.quantize_model(), which leverages simulated quantization operations inserted into the computation graph. This allows models to learn weight distributions more robust to reduced precision, thereby improving accuracy when deployed with INT8 inference.

In PyTorch, PTQ is performed using torch.quantization.convert(), which transforms a pre-trained model into a quantized version optimized for inference. PyTorch supports both dynamic and static quantization, enabling trade-offs between accuracy and efficiency. QAT in PyTorch is facilitated using torch.quantization.prepare_qat(), which introduces fake quantization layers during training to simulate low-precision arithmetic while maintaining full-precision gradients. This approach helps the model adapt to quantization constraints without incurring substantial accuracy loss.

ONNX Runtime supports PTQ through onnxruntime.quantization, which includes both static and dynamic quantization modes. While static quantization relies on calibration data to determine optimal scaling factors for weights and activations, dynamic quantization applies quantization only during inference, offering flexibility for real-time applications. For QAT, ONNX Runtime provides onnxruntime.training.QuantizationMode.QAT, allowing models to be trained with simulated quantization prior to export for INT8 inference.

Although PTQ offers a straightforward and computationally inexpensive means to optimize models, it may lead to accuracy degradation—especially for sensitivity-critical architectures. QAT, despite its higher training cost, delivers models that better preserve accuracy when deployed under low-precision computations.

Choosing between PTQ and QAT

Quantization plays a critical role in optimizing machine learning models for deployment on low-precision hardware, enabling smaller model sizes, faster inference, and reduced power consumption. The choice between PTQ and QAT depends on the trade-offs between accuracy, computational cost, and deployment constraints.

PTQ is the preferred approach when retraining is infeasible or unnecessary. It is computationally inexpensive, requiring only a conversion step after training, making it an efficient way to optimize models for inference. However, its effectiveness varies across model architectures—CNNs for image classification often tolerate PTQ well, while NLP and speech models may experience accuracy degradation due to their reliance on precise numerical representations.

QAT, in contrast, is necessary when high accuracy retention is critical. By integrating quantization effects during training, QAT allows models to adapt to lower-precision arithmetic, reducing quantization errors. While this results in higher accuracy in low-precision inference, it also requires additional training time and computational resources, making it less practical for cases where fast model deployment is a priority (Jacob et al. 2018b).

Ultimately, the decision between PTQ and QAT depends on the specific requirements of the machine learning system. If rapid deployment and minimal computational overhead are the primary concerns, PTQ provides a quick and effective solution. If accuracy is a critical factor and the model is sensitive to quantization errors, QAT offers a more robust but computationally expensive alternative. In many real-world applications, a hybrid approach that starts with PTQ and selectively applies QAT for accuracy-critical models provides the best balance between efficiency and performance.

10.5.6 Extreme Precision Reduction

Extreme precision reduction techniques, such as binarization and ternarization, are designed to dramatically reduce the bit-width of weights and activations in a neural network. By representing values with just one or two bits (for binary and ternary representations, respectively), these techniques achieve substantial reductions in memory usage and computational requirements, making them particularly attractive for hardware-efficient deployment in resource-constrained environments (Courbariaux, Bengio, and David 2016).

Courbariaux, Matthieu, Yoshua Bengio, and Jean-Pierre David. 2016. “BinaryConnect: Training Deep Neural Networks with Binary Weights During Propagations.” Advances in Neural Information Processing Systems (NeurIPS) 28: 3123–31.

Binarization

Binarization involves reducing weights and activations to just two values, typically -1 and +1, or 0 and 1, depending on the specific method. The primary advantage of binarization lies in its ability to drastically reduce the size of a model, allowing it to fit into a very small memory footprint. This reduction also accelerates inference, especially when deployed on specialized hardware such as binary neural networks (Rastegari et al. 2016). However, binarization introduces significant challenges, primarily in terms of model accuracy. When weights and activations are constrained to only two values, the expressiveness of the model is greatly reduced, which can lead to a loss in accuracy, particularly in tasks requiring high precision, such as image recognition or natural language processing (Hubara et al. 2018).

Rastegari, Mohammad, Vicente Ordonez, Joseph Redmon, and Ali Farhadi. 2016. “XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks.” In Computer Vision – ECCV 2016, 525–42. Springer International Publishing. https://doi.org/10.1007/978-3-319-46493-0\_32.

Hubara, Itay, Matthieu Courbariaux, Daniel Soudry, Ran El-Yaniv, and Yoshua Bengio. 2018. “Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations.” Journal of Machine Learning Research (JMLR) 18: 1–30.

Bengio, Yoshua, Nicholas Léonard, and Aaron Courville. 2013b. “Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation.” arXiv Preprint, August. http://arxiv.org/abs/1308.3432v1.

Moreover, the process of binarization introduces non-differentiable operations, which complicates the optimization process. To address this issue, techniques such as the STE are employed to approximate gradients, allowing for effective backpropagation despite the non-differentiability of the quantization operation (Y. Bengio, Léonard, and Courville 2013b). The use of STE ensures that the network can still learn and adjust during training, even with the extreme precision reduction. While these challenges are non-trivial, the potential benefits of binarized models in ultra-low-power environments, such as edge devices and IoT sensors, make binarization an exciting area of research.

Ternarization

Ternarization extends binarization by allowing three possible values for weights and activations—typically -1, 0, and +1. While ternarization still represents a significant reduction in precision, it offers a slight improvement in model accuracy over binarization, as the additional value (0) provides more flexibility in capturing the underlying patterns (Zhu et al. 2017). This additional precision comes at the cost of increased complexity, both in terms of computation and the required training methods. Similar to binarization, ternarization is often implemented using techniques that approximate gradients, such as the hard thresholding method or QAT, which integrate quantization effects into the training process to mitigate the accuracy loss (Choi et al. 2018).

Zhu, Chenzhuo, Song Han, Huizi Mao, and William J. Dally. 2017. “Trained Ternary Quantization.” International Conference on Learning Representations (ICLR).

Choi, Jungwook, Zhuo Wang, Swagath Venkataramani, Pierce I-Jen Chuang, Vijayalakshmi Srinivasan, and Kailash Gopalakrishnan. 2018. “PACT: Parameterized Clipping Activation for Quantized Neural Networks.” arXiv Preprint, May. http://arxiv.org/abs/1805.06085v2.

Li, Fengfu, Bin Liu, Xiaoxing Wang, Bo Zhang, and Junchi Yan. 2016. “Ternary Weight Networks.” arXiv Preprint, May. http://arxiv.org/abs/1605.04711v3.

The advantages of ternarization over binarization are most noticeable when dealing with highly sparse data. In some cases, ternarization can introduce more sparsity into the model by mapping a large portion of weights to zero. However, managing this sparsity effectively requires careful implementation to avoid the overhead that comes with storing sparse matrices (F. Li et al. 2016). Additionally, while ternarization improves accuracy compared to binarization, it still represents a severe trade-off in terms of the model’s ability to capture intricate relationships between inputs and outputs. The challenge, therefore, lies in finding the right balance between the memory and computational savings offered by ternarization and the accuracy loss incurred by reducing the precision.

Challenges and Limitations

What makes binarization and ternarization particularly interesting is their potential to enable ultra-low-power machine learning. These extreme precision reduction methods offer a way to make machine learning models more feasible for deployment on hardware with strict resource constraints, such as embedded systems and mobile devices. However, the challenge remains in how to maintain the performance of these models despite such drastic reductions in precision. Binarized and ternarized models require specialized hardware that is capable of efficiently handling binary or ternary operations. Many traditional processors are not optimized for this type of computation, which means that realizing the full potential of these methods often requires custom hardware accelerators (Umuroglu et al. 2017).

Umuroglu, Yaman, Nicholas J. Fraser, Giulio Gambardella, Michaela Blott, Philip Leong, Magnus Jahre, and Kees Vissers. 2017. “FINN: A Framework for Fast, Scalable Binarized Neural Network Inference.” In Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, 65–74. ACM. https://doi.org/10.1145/3020078.3021744.

Jacob, Benoit, Skirmantas Kligys, Bo Chen, Menglong Zhu, Matthew Tang, Andrew Howard, Hartwig Adam, and Dmitry Kalenichenko. 2018b. “Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference.” In 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2704–13. IEEE. https://doi.org/10.1109/cvpr.2018.00286.

Another challenge is the loss of accuracy that typically accompanies the extreme precision reduction inherent in binarization and ternarization. These methods are best suited for tasks where high levels of precision are not critical, or where the model can be trained to adjust to the precision constraints through techniques like QAT. Despite these challenges, the ability to drastically reduce the size of a model while maintaining acceptable levels of accuracy makes binarization and ternarization attractive for certain use cases, particularly in edge AI and resource-constrained environments (Jacob et al. 2018b).

The future of these techniques lies in advancing both the algorithms and hardware that support them. As more specialized hardware is developed for low-precision operations, and as techniques for compensating for precision loss during training improve, binarization and ternarization will likely play a significant role in making AI models more efficient, scalable, and energy-efficient.

10.5.7 Quantization vs. Model Representation

Thus far, we explored various quantization techniques, including PTQ, QAT, and extreme precision reduction methods like binarization and ternarization. These techniques aim to reduce the memory footprint and computational demands of machine learning models, making them suitable for deployment in environments with strict resource constraints, such as edge devices or mobile platforms.

While quantization offers significant reductions in model size and computational requirements, it often requires careful management of the trade-offs between model efficiency and accuracy. When comparing quantization to other model representation techniques—such as pruning, knowledge distillation, and NAS—several key differences and synergies emerge.

Pruning focuses on reducing the number of parameters in a model by removing unimportant or redundant weights. While quantization reduces the precision of weights and activations, pruning reduces their sheer number. The two techniques can complement each other: pruning can be applied first to reduce the number of weights, which then makes the quantization process more effective by working with a smaller set of parameters. However, pruning does not necessarily reduce precision, so it may not achieve the same level of computational savings as quantization.

Knowledge distillation reduces model size by transferring knowledge from a large, high-precision model (teacher) to a smaller, more efficient model (student). While quantization focuses on precision reduction within a given model, distillation works by transferring learned behavior into a more compact model. The advantage of distillation is that it can help mitigate accuracy loss, which is often a concern with extreme precision reduction. When combined with quantization, distillation can help ensure that the smaller, quantized model retains much of the accuracy of the original, larger model.

NAS automates the design of neural network architectures to identify the most efficient model for a given task. NAS focuses on optimizing the structure of the model itself, whereas quantization operates on the numerical representation of the model’s weights and activations. The two approaches can be complementary, as NAS can lead to model architectures that are inherently more suited for low-precision operations, thus making quantization more effective. In this sense, NAS can be seen as a precursor to quantization, as it optimizes the architecture for the constraints of low-precision environments.

As shown in Figure 10.22, different compression strategies such as pruning, quantization, and singular value decomposition (SVD) exhibit varying trade-offs between model size and accuracy loss. While pruning combined with quantization (red circles) achieves high compression ratios with minimal accuracy loss, quantization alone (yellow squares) also provides a reasonable balance. In contrast, SVD (green diamonds) requires a larger model size to maintain accuracy, illustrating how different techniques can impact compression effectiveness.

Figure 10.22: Accuracy vs. compression rate under different compression methods. Source: Han, Mao, and Dally (2015).

In summary, quantization differs from pruning, knowledge distillation, and NAS in that it specifically focuses on reducing the numerical precision of weights and activations. While quantization alone can provide significant computational benefits, its effectiveness can be amplified when combined with the complementary techniques of pruning, distillation, and NAS. These methods, each targeting a different aspect of model efficiency, work together to create more compact, faster, and energy-efficient models, enabling better performance in constrained environments. By understanding the strengths and limitations of these methods, practitioners can choose the most suitable combination to meet the specific needs of their application and deployment hardware.

10.6 Optimizing Architectural Efficiency

Architectural efficiency is the process of optimizing the machine learning model structures with an explicit focus on the computational resources available during deployment. Unlike other optimization methods, such as pruning and knowledge distillation, which are applied after model training and are agnostic to the hardware on which the model will run, architectural efficiency requires proactive consideration of the target hardware from the beginning. This approach ensures that models are designed to effectively utilize the specific capabilities of the deployment platform, whether it be a mobile device, embedded system, or specialized AI hardware.

10.6.1 Hardware-Aware Model Design

The incorporation of hardware constraints—such as memory bandwidth, processing power, and energy consumption—into model design enables the creation of architectures that are both accurate and computationally efficient. This approach leads to improved performance and reduced resource usage during both training and inference.

The focus of this section is on the techniques that can be employed to achieve architectural efficiency, including exploiting sparsity, model factorization, dynamic computation, and hardware-aware design. These techniques allow for the development of models that are optimized for the constraints of specific hardware environments, ensuring that they can operate efficiently and meet the performance requirements of real-world applications.

Principles of Efficient Design

Designing machine learning models for hardware efficiency involves structuring architectures with consideration for specific hardware constraints such as computational cost, memory usage, inference latency, and power consumption, while still maintaining strong predictive performance. Unlike post-training optimizations, which attempt to recover efficiency after a model has been trained, hardware-aware model design takes hardware considerations into account from the outset. This ensures that models are computationally efficient and can be deployed across diverse hardware environments with minimal adaptation.

Efficient hardware-aware design focuses on leveraging the strengths of specific hardware platforms (e.g., GPUs, TPUs, mobile devices, or edge devices) to ensure that the model is optimized for the hardware on which it will be deployed. This means designing models that can fully exploit hardware accelerators’ parallelism, memory hierarchies, and power efficiency, and reduce latency through hardware-optimized operations.

To systematically understand the key aspects of hardware-aware model design, we can organize these principles into broad categories that address different computational and system constraints. The following table outlines key hardware-aware design principles, which we will explore in greater depth:

Table 10.9: Taxonomy of hardware-aware model design principles.

Principle	Goal	Example Networks
Scaling Optimization	Adjust model depth, width, and resolution to balance efficiency and hardware constraints.	EfficientNet, RegNet
Computation Reduction	Minimize redundant operations to reduce computational cost, utilizing hardware-specific optimizations (e.g., using depthwise separable convolutions on mobile chips).	MobileNet, ResNeXt
Memory Optimization	Ensure efficient memory usage by reducing activation and parameter storage requirements, leveraging hardware-specific memory hierarchies (e.g., local and global memory in GPUs).	DenseNet, SqueezeNet
Hardware-Aware Design	Optimize architectures for specific hardware constraints (e.g., low power, parallelism, high throughput).	TPU-optimized models, MobileNet

Each of these categories addresses a fundamental aspect of hardware-aware model efficiency. Scaling optimization ensures that models are not over- or under-parameterized relative to the available hardware resources. This helps optimize performance while ensuring efficient resource usage. Computation reduction techniques focus on eliminating redundant operations that consume excessive computational resources, and they can be tailored to specific hardware features like parallelism (e.g., using depthwise separable convolutions on mobile CPUs or GPUs). Memory optimization ensures that memory resources are efficiently utilized, considering hardware-specific memory hierarchies such as cache and on-chip memory. Dynamic computation techniques enable models to adjust their inference complexity based on the input, which is particularly beneficial for real-time applications where hardware constraints (like power) are critical. Finally, hardware-aware design principles align architectural decisions with hardware capabilities, making sure that the model’s structure is fully optimized for the hardware it runs on, maximizing execution efficiency and minimizing power consumption.

Scaling Optimization

Scaling a model’s architecture involves balancing accuracy with computational cost, and optimizing it to align with the capabilities of the target hardware. Each component of a model, whether its depth, width, or input resolution, impacts resource consumption. In hardware-aware design, these dimensions should not only be optimized for accuracy but also for efficiency in memory usage, processing power, and energy consumption, especially when the model is deployed on specific hardware like GPUs, TPUs, or edge devices.

From a hardware-aware perspective, it is crucial to consider how different hardware platforms, such as GPUs, TPUs, or edge devices, interact with scaling dimensions. For instance, deeper models can capture more complex representations, but excessive depth can lead to increased inference latency, longer training times, and higher memory consumption—issues that are particularly problematic on resource-constrained platforms. Similarly, increasing the width of the model to process more parallel information may be beneficial for GPUs and TPUs with high parallelism, but it requires careful management of memory usage. In contrast, increasing the input resolution can provide finer details for tasks like image classification, but it exponentially increases computational costs, potentially overloading hardware memory or causing power inefficiencies on edge devices.

Mathematically, the total FLOPs for a convolutional model can be approximated as:

\[ \text{FLOPs} \propto d \cdot w^2 \cdot r^2, \]

where $d$ is depth, $w$ is width, and $r$ is the input resolution. Increasing all three dimensions without considering the hardware limitations can result in suboptimal performance, especially on devices with limited computational power or memory bandwidth.

For efficient model scaling, it’s essential to manage these parameters in a balanced way, ensuring that the model remains within the limits of the hardware while maximizing performance. This is where compound scaling comes into play. Instead of adjusting depth, width, and resolution independently, compound scaling balances all three dimensions together by applying fixed ratios $(\alpha, \beta, \gamma)$ relative to a base model:

\[ d = \alpha^\phi d_0, \quad w = \beta^\phi w_0, \quad r = \gamma^\phi r_0 \]

Here, $\phi$ is a scaling coefficient, and $\alpha$, $\beta$, and $\gamma$ are scaling factors determined based on hardware constraints and empirical data. This approach ensures that models grow in a way that optimizes hardware resource usage, keeping them efficient while improving accuracy.

For example, EfficientNet, which employs compound scaling, demonstrates how carefully balancing depth, width, and resolution results in models that are both computationally efficient and high-performing. Compound scaling reduces computational cost while preserving accuracy, making it a key consideration for hardware-aware model design. This approach is particularly beneficial when deploying models on GPUs or TPUs, where parallelism can be fully leveraged, but memory and power usage need to be carefully managed.

This principle applies not only to convolutional models but also to other architectures like transformers. For instance, in transformer models, adjusting the number of attention heads or layers can have similar resource usage implications, and hardware-aware scaling can ensure that the computational cost is minimized while maintaining strong performance.

Beyond convolutional models, this principle of scaling optimization can be generalized to other architectures, such as transformers. In these architectures, adjusting the number of layers, attention heads, or embedding dimensions can have a similar impact on computational efficiency. Hardware-aware scaling has become a central consideration in optimizing model performance for various computational constraints, particularly when working with large models or resource-constrained devices.

Computation Reduction

Reducing redundant operations is a critical strategy for improving the efficiency of machine learning models, especially when considering deployment on resource-constrained hardware. Traditional machine learning architectures, particularly convolutional neural networks, often rely on dense operations—such as standard convolutions—which apply computations uniformly across all spatial locations and channels. However, these operations introduce unnecessary computation, especially when many of the channels or activations do not contribute meaningfully to the final prediction. This can lead to excessive computational load and memory consumption, which are significant constraints on hardware with limited processing power or memory bandwidth, like mobile or embedded devices.

To address this issue, modern architectures leverage factorized computations, which decompose complex operations into simpler components. This enables models to achieve the same representational power while reducing the computational overhead, making them more efficient for deployment on specific hardware platforms. One widely adopted method for computation reduction is depthwise separable convolutions, introduced in the MobileNet architecture. Depthwise separable convolutions break a standard convolution operation into two distinct steps:

Depthwise convolution applies a separate convolutional filter to each input channel independently, ensuring that computations for each channel are treated separately.
Pointwise convolution (a 1x1 convolution) then mixes the outputs across channels, effectively combining the results into the final feature representation.

This factorization reduces the number of operations compared to the standard convolutional approach, where a single filter processes all input channels simultaneously. The reduction in operations is particularly beneficial for hardware accelerators, as it reduces the number of calculations that need to be performed and the amount of memory bandwidth required. The computational complexity of a standard convolution with an input size of $h \times w$, $C_{\text{in}}$ input channels, and $C_{\text{out}}$ output channels can be expressed as:

\[ \mathcal{O}(h w C_{\text{in}} C_{\text{out}} k^2) \]

where $k$ is the kernel size. This equation shows that the computational cost scales with both the spatial dimensions and the number of channels, making it computationally expensive. However, for depthwise separable convolutions, the complexity reduces to:

\[ \mathcal{O}(h w C_{\text{in}} k^2) + \mathcal{O}(h w C_{\text{in}} C_{\text{out}}) \]

Here, the first term depends only on $C_{\text{in}}$, the number of input channels, and the second term eliminates the $k^2$ factor from the channel-mixing operation. The result is a 5× to 10× reduction in FLOPs (floating-point operations), which directly reduces the computational burden and improves model efficiency, particularly for hardware with limited resources, such as mobile devices or edge processors.

Beyond depthwise separable convolutions, other architectures employ additional factorization techniques to further reduce computation. For example, Grouped convolutions, used in the ResNeXt architecture, split feature maps into separate groups, each of which is processed independently before being merged. This approach increases computational efficiency while maintaining strong accuracy by reducing redundant operations. Another example is Bottleneck layers, used in architectures like ResNet. These layers employ 1×1 convolutions to reduce the dimensionality of feature maps before applying larger convolutions, which reduces the computational complexity of deeper networks, where most of the computational cost lies.

These computation reduction techniques are highly effective in optimizing models for specific hardware, particularly for real-time applications in mobile, edge computing, and embedded systems. By reducing the number of computations required, models can achieve high performance while consuming fewer resources, which is critical for ensuring low inference latency and minimal energy usage.

In hardware-aware model design, such as when deploying on GPUs, TPUs, or other specialized accelerators, these techniques can significantly reduce computational load and memory footprint. By reducing the complexity of operations, the hardware can process the data more efficiently, allowing for faster execution and lower power consumption. Additionally, these techniques can be combined with other optimizations, such as sparsity, to maximize hardware utilization and achieve better overall performance.

Memory Optimization

Memory optimization is a fundamental aspect of model efficiency, especially when deploying machine learning models on resource-constrained hardware, such as mobile devices, embedded systems, and edge AI platforms. Inference-based models require memory to store activations, intermediate feature maps, and parameters. If these memory demands exceed the hardware’s available resources, the model can experience performance bottlenecks, including increased inference latency and power inefficiencies due to frequent memory accesses. Efficient memory management is crucial to minimize these issues while maintaining accuracy and performance.

To address these challenges, modern architectures employ various memory-efficient strategies that reduce unnecessary storage while keeping the model’s performance intact. Hardware-aware memory optimization techniques are particularly important when considering deployment on accelerators such as GPUs, TPUs, or edge AI chips. These strategies ensure that models are computationally tractable and energy-efficient, particularly when operating under strict power and memory constraints.

One effective technique for memory optimization is feature reuse, a strategy employed in DenseNet. In traditional convolutional networks, each layer typically computes a new set of feature maps, increasing the model’s memory footprint. However, DenseNet reduces the need for redundant activations by reusing feature maps from previous layers and selectively applying transformations. This method reduces the total number of feature maps that need to be stored, which in turn lowers the memory requirements without sacrificing accuracy. In a standard convolutional network with $L$ layers, if each layer generates $k$ new feature maps, the total number of feature maps grows linearly:

\[ \mathcal{O}(L k) \]

In contrast, DenseNet reuses feature maps from earlier layers, reducing the number of feature maps stored. This leads to improved parameter efficiency and a reduced memory footprint, which is essential for hardware with limited memory resources.

Another useful technique is activation checkpointing, which is especially beneficial during training. In a typical neural network, backpropagation requires storing all forward activations for the backward pass. This can lead to a significant memory overhead, especially for large models. Activation checkpointing reduces memory consumption by only storing a subset of activations and recomputing the remaining ones when needed. If an architecture requires storing $A_{\text{total}}$ activations, the standard backpropagation method requires the full storage:

\[ \mathcal{O}(A_{\text{total}}) \]

With activation checkpointing, however, only a fraction of activations is stored, and the remaining ones are recomputed on-the-fly, reducing storage requirements to:

\[ \mathcal{O}(\sqrt{A_{\text{total}}}) \]

This technique can significantly reduce peak memory consumption, making it particularly useful for training large models on hardware with limited memory.

Parameter reduction is another essential technique, particularly for models that use large filters. For instance, SqueezeNet uses a novel architecture where it applies 1x1 convolutions to reduce the number of input channels before applying standard convolutions. By first reducing the number of channels with 1x1 convolutions, SqueezeNet reduces the model size significantly without compromising the model’s expressive power. The number of parameters in a standard convolutional layer is:

\[ \mathcal{O}(C_{\text{in}} C_{\text{out}} k^2) \]

By reducing $C_{\text{in}}$ using 1x1 convolutions, SqueezeNet reduces the number of parameters, achieving a 50x reduction in model size compared to AlexNet while maintaining similar performance. This method is particularly valuable for edge devices that have strict memory and storage constraints.

These memory-efficient techniques—feature reuse, activation checkpointing, and parameter reduction—are key components of hardware-aware model design. By minimizing memory usage and efficiently managing storage, these techniques allow machine learning models to fit within the memory limits of modern accelerators, such as GPUs, TPUs, and edge devices. These strategies also lead to lower power consumption by reducing the frequency of memory accesses, which is particularly beneficial for devices with limited battery life.

In hardware-aware design, memory optimization is not just about reducing memory usage but also about optimizing how memory is accessed. Specialized accelerators like TPUs and GPUs can take advantage of memory hierarchies, caching, and high bandwidth memory to efficiently handle sparse or reduced-memory representations. By incorporating these memory-efficient strategies, models can operate with minimal overhead, enabling faster inference and more efficient power consumption.

10.6.2 Dynamic Computation and Adaptation

Dynamic computation refers to the ability of a machine learning model to adapt its computational load based on the complexity of the input. Rather than applying a fixed amount of computation to every input, dynamic computation allows models to allocate computational resources more effectively, depending on the task’s requirements. This is especially crucial for applications where computational efficiency, real-time processing, and energy conservation are vital, such as in mobile devices, embedded systems, and autonomous vehicles.

In traditional machine learning models, every input is processed using the same network architecture, irrespective of its complexity. For example, an image classification model might apply the full depth of a neural network to classify both a simple and a complex image, even though the simple image could be classified with fewer operations. This uniform processing results in wasted computational resources, unnecessary power consumption, and increased processing times—all of which are particularly problematic in real-time and resource-constrained systems.

Dynamic computation addresses these inefficiencies by allowing models to adjust the computational load based on the input’s complexity. For simpler inputs, the model might skip certain layers or operations, reducing computational costs. On the other hand, for more complex inputs, it may opt to process additional layers or operations to ensure accuracy is maintained. This adaptive approach not only optimizes computational efficiency but also reduces energy consumption, minimizes latency, and preserves high predictive performance.

Dynamic computation is essential for efficient resource use on hardware with limited capabilities. Adjusting the computational load dynamically based on input complexity enables models to significantly enhance efficiency and overall performance without sacrificing accuracy.

Dynamic Schemes

Dynamic schemes enable models to selectively reduce computation when inputs are simple, preserving resources while maintaining predictive performance. The approaches discussed below, beginning with early exit architectures, illustrate how to implement this adaptive strategy effectively.

Early Exit Architectures

Early exit architectures allow a model to make predictions at intermediate points in the network rather than completing the full forward pass for every input. This approach is particularly effective for real-time applications and energy-efficient inference, as it enables selective computation based on the complexity of individual inputs (Teerapittayanon, McDanel, and Kung 2017).

The core mechanism in early exit architectures involves multiple exit points embedded within the network. Simpler inputs, which can be classified with high confidence early in the model, exit at an intermediate layer, reducing unnecessary computations. Conversely, more complex inputs continue processing through deeper layers to ensure accuracy.

A well-known example is BranchyNet, which introduces multiple exit points throughout the network. For each input, the model evaluates intermediate predictions using confidence thresholds. If the prediction confidence exceeds a predefined threshold at an exit point, the model terminates further computations and outputs the result. Otherwise, it continues processing until the final layer (Teerapittayanon, McDanel, and Kung 2017). This approach minimizes inference time without compromising performance on challenging inputs.

Teerapittayanon, Surat, Bradley McDanel, and H. T. Kung. 2017. “BranchyNet: Fast Inference via Early Exiting from Deep Neural Networks.” arXiv Preprint arXiv:1709.01686, September. http://arxiv.org/abs/1709.01686v1.

Scardapane, Simone, Ye Wang, and Massimo Panella. 2020. “Why Should i Trust You? A Survey of Explainability of Machine Learning for Healthcare.” Pattern Recognition Letters 140: 47–57.

Another example is multi-exit vision transformers, which extend early exits to transformer-based architectures. These models use lightweight classifiers at various transformer layers, allowing predictions to be generated early when possible (Scardapane, Wang, and Panella 2020). This technique significantly reduces inference time while maintaining robust performance for complex samples.

Early exit models are particularly advantageous for resource-constrained devices, such as mobile processors and edge accelerators. By dynamically adjusting computational effort, these architectures reduce power consumption and processing latency, making them ideal for real-time decision-making (Hu, Zhang, and Fu 2021).

Hu, Bowen, Zhiqiang Zhang, and Yun Fu. 2021. “Triple Wins: Boosting Accuracy, Robustness and Efficiency Together by Enabling Input-Adaptive Inference.” Advances in Neural Information Processing Systems 34: 18537–50.

Yu, Jun, Peng Li, and Zhenhua Wang. 2023. “Efficient Early Exiting Strategies for Neural Network Acceleration.” IEEE Transactions on Neural Networks and Learning Systems.

When deployed on hardware accelerators such as GPUs and TPUs, early exit architectures can be further optimized by exploiting parallelism. For example, different exit paths can be processed simultaneously, enhancing throughput while maintaining adaptive computation (Yu, Li, and Wang 2023).

Conditional Computation

Conditional computation refers to the ability of a neural network to decide which parts of the model to activate based on the input, thereby reducing unnecessary computation. This approach can be highly beneficial in resource-constrained environments, such as mobile devices or real-time systems, where reducing the number of operations directly translates to lower computational cost, power consumption, and inference latency (E. Bengio et al. 2015).

Bengio, Emmanuel, Pierre-Luc Bacon, Joelle Pineau, and Doina Precup. 2015. “Conditional Computation in Neural Networks for Faster Models.” arXiv Preprint arXiv:1511.06297, November. http://arxiv.org/abs/1511.06297v2.

In contrast to Early Exit Architectures, where the decision to exit early is typically made once a threshold confidence level is met, conditional computation works by dynamically selecting which layers, units, or paths in the network should be computed based on the characteristics of the input. This can be achieved through mechanisms such as gating functions or dynamic routing, which essentially “turn off” parts of the network that are not needed for a particular input, allowing the model to focus computational resources where they are most required.

One example of conditional computation is SkipNet, which uses a gating mechanism to skip layers in a CNN when the input is deemed simple enough. The gating mechanism uses a lightweight classifier to predict if the layer should be skipped. This prediction is made based on the input, and the model adjusts the number of layers used during inference accordingly (X. Wang et al. 2018). If the gating function determines that the input is simple, certain layers are bypassed, resulting in faster inference. However, for more complex inputs, the model uses the full depth of the network to achieve the necessary accuracy.

Wang, Xin, Fisher Yu, Zi-Yi Dou, Trevor Darrell, and Joseph E. Gonzalez. 2018. “SkipNet: Learning Dynamic Routing in Convolutional Networks.” In Computer Vision – ECCV 2018, 420–36. Springer; Springer International Publishing. https://doi.org/10.1007/978-3-030-01261-8\_25.

Sabour, Sara, Nicholas Frosst, and Geoffrey E Hinton. 2017. “Dynamic Routing Between Capsules.” In Advances in Neural Information Processing Systems. Vol. 30.

Another example is Dynamic Routing Networks, such as in the Capsule Networks (CapsNets), where routing mechanisms dynamically choose the path that activations take through the network. In these networks, the decision-making process involves selecting specific pathways for information flow based on the input’s complexity, which can significantly reduce the number of operations and computations required (Sabour, Frosst, and Hinton 2017). This mechanism introduces adaptability by leveraging different routing strategies, providing computational efficiency while preserving the quality of predictions.

These conditional computation strategies have significant advantages in real-world applications where computational resources are limited. For example, in autonomous driving, the system must process a variety of inputs (e.g., pedestrians, traffic signs, road lanes) with varying complexity. In cases where the input is straightforward, a simpler, less computationally demanding path can be taken, whereas more complex scenarios (such as detecting obstacles or performing detailed scene understanding) will require full use of the model’s capacity. Conditional computation ensures that the system adapts its computation based on the real-time complexity of the input, leading to improved speed and efficiency (Huang, Chen, and Zhang 2023).

Huang, Wei, Jie Chen, and Lei Zhang. 2023. “Adaptive Neural Networks for Real-Time Processing in Autonomous Systems.” IEEE Transactions on Intelligent Transportation Systems.

Gate-Based Conditional Computation

Gate-based conditional computation introduces learned gating mechanisms that dynamically control which parts of a neural network are activated based on input complexity. Unlike static architectures that process all inputs with the same computational effort, this approach learns decision boundaries during training, allowing models to selectively activate different sub-networks or layers (Shazeer et al. 2017).

Gating mechanisms are typically implemented using binary or continuous gating functions, where a lightweight control network predicts whether a particular layer or path should be executed. This decision-making process occurs dynamically at inference time, enabling models to allocate resources efficiently.

A well-known example is the Dynamic Filter Network (DFN), which applies input-dependent filtering by selecting different convolutional kernels at runtime. Instead of applying the same filters to all inputs, DFN adapts its filter selection, reducing computation for simpler inputs while maintaining high expressiveness for more complex cases (Jia et al. 2016).

Jia, Xu, Bert De Brabandere, Tinne Tuytelaars, and Luc Van Gool. 2016. “Dynamic Filter Networks.” Advances in Neural Information Processing Systems 29.

Shazeer, Noam, Azalia Mirhoseini, Piotr Maziarz, et al. 2017. “Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer.” In International Conference on Learning Representations.

Fedus, William, Barret Zoph, and Noam Shazeer. 2021. “Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity.” Journal of Machine Learning Research.

Another example is the Mixture of Experts (MoE) framework, where a gating network determines which subset of “expert” subnetworks should be activated for a given input. Rather than engaging the entire model, MoE dynamically routes inputs to a small, specialized subset of experts, significantly improving computational efficiency while maintaining model flexibility (Shazeer et al. 2017). This architecture has been widely used in large-scale transformer models, including Google’s Switch Transformer, to optimize both inference speed and scalability (Fedus, Zoph, and Shazeer 2021).

Gate-based conditional computation is particularly useful for multi-task learning and transfer learning, where different inputs may require specialized processing. By dynamically selecting the most relevant components, these models can optimize efficiency without sacrificing accuracy.

However, this approach introduces additional computational complexity due to the overhead of evaluating gating functions at inference time. Efficient implementation on specialized hardware (e.g., TPUs, GPUs, or edge accelerators) requires careful optimization to minimize latency while maintaining adaptability (Lepikhin et al. 2020).

Lepikhin, Dmitry et al. 2020. “GShard: Scaling Giant Models with Conditional Computation.” In Proceedings of the International Conference on Learning Representations.

Adaptive Inference

Adaptive inference refers to a model’s ability to dynamically adjust its computational effort during inference based on input complexity. Unlike earlier approaches that rely on predefined exit points or discrete layer skipping, adaptive inference continuously modulates computational depth and resource allocation based on real-time confidence and task complexity (Yang et al. 2020).

Yang, Le, Yizeng Han, Xi Chen, Shiji Song, Jifeng Dai, and Gao Huang. 2020. “Resolution Adaptive Networks for Efficient Inference.” In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2366–75. IEEE. https://doi.org/10.1109/cvpr42600.2020.00244.

This flexibility allows models to make on-the-fly decisions about how much computation is required, balancing efficiency and accuracy without rigid thresholds. Instead of committing to a fixed computational path, adaptive inference enables models to dynamically allocate layers, operations, or specialized computations based on intermediate assessments of the input (Yang et al. 2020).

One example of adaptive inference is Fast Neural Networks (FNNs), which adjust the number of active layers based on real-time complexity estimation. If an input is deemed straightforward, only a subset of layers is activated, reducing inference time. However, if early layers produce low-confidence outputs, additional layers are engaged to refine the prediction (Jian Wu, Cheng, and Zhang 2019).

Wu, Jian, Hao Cheng, and Yifan Zhang. 2019. “Fast Neural Networks: Efficient and Adaptive Computation for Inference.” In Advances in Neural Information Processing Systems.

Contro, Filippo, Marco Crosara, Mariano Ceccato, and Mila Dalla Preda. 2021. “EtherSolve: Computing an Accurate Control-Flow Graph from Ethereum Bytecode.” arXiv Preprint arXiv:2103.09113, March. http://arxiv.org/abs/2103.09113v1.

A related approach is dynamic layer scaling, where models progressively increase computational depth based on uncertainty estimates. This technique is particularly useful for fine-grained classification tasks, where some inputs require only coarse-grained processing while others need deeper feature extraction (Contro et al. 2021).

Adaptive inference is particularly effective in latency-sensitive applications where resource constraints fluctuate dynamically. For instance, in autonomous systems, tasks such as lane detection may require minimal computation, while multi-object tracking in dense environments demands additional processing power. By adjusting computational effort in real-time, adaptive inference ensures that models operate within strict timing constraints without unnecessary resource consumption.

On hardware accelerators such as GPUs and TPUs, adaptive inference leverages parallel processing capabilities by distributing workloads dynamically. This adaptability maximizes throughput while minimizing energy expenditure, making it ideal for real-time, power-sensitive applications.

Challenges and Limitations

Dynamic computation introduces flexibility and efficiency by allowing models to adjust their computational workload based on input complexity. However, this adaptability comes with several challenges that must be addressed to make dynamic computation practical and scalable. These challenges arise in training, inference efficiency, hardware execution, generalization, and evaluation, each presenting unique difficulties that impact model design and deployment.

Training Complexity and Optimization Difficulties

Unlike standard neural networks, which follow a fixed computational path for every input, dynamic computation requires additional control mechanisms, such as gating networks, confidence estimators, or expert selection strategies. These mechanisms determine which parts of the model should be activated or skipped, adding complexity to the training process. One major difficulty is that many of these decisions are discrete, meaning they cannot be optimized using standard backpropagation. Instead, models often rely on techniques like reinforcement learning or continuous approximations, but these approaches introduce additional computational costs and can slow down convergence.

Training dynamic models also presents instability because different inputs follow different paths, leading to inconsistent gradient updates across training examples. This variability can make optimization less efficient, requiring careful regularization strategies to maintain smooth learning dynamics. Additionally, dynamic models introduce new hyperparameters, such as gating thresholds or confidence scores for early exits. Selecting appropriate values for these parameters is crucial to ensuring the model effectively balances accuracy and efficiency, but it significantly increases the complexity of the training process.

Inference Overhead and Latency Variability

Although dynamic computation reduces unnecessary operations, the process of determining which computations to perform introduces additional overhead. Before executing inference, the model must first decide which layers, paths, or subnetworks to activate. This decision-making process, often implemented through lightweight gating networks, adds computational cost and can partially offset the savings gained by skipping computations. While these overheads are usually small, they become significant in resource-constrained environments where every operation matters.

An even greater challenge is the variability in inference time. In static models, inference follows a fixed sequence of operations, leading to predictable execution times. In contrast, dynamic models exhibit variable processing times depending on input complexity. For applications with strict real-time constraints, such as autonomous driving or robotics, this unpredictability can be problematic. A model that processes some inputs in milliseconds but others in significantly longer time frames may fail to meet strict latency requirements, limiting its practical deployment.

Hardware Execution Inefficiencies

Modern hardware accelerators, such as GPUs and TPUs, are designed for uniform, parallel computation. They achieve efficiency by executing the same operations across large batches of data. Dynamic computation disrupts this by introducing conditional branching, which leads to inefficient utilization of hardware resources. Since different inputs follow different paths, some computational units may remain idle, reducing overall throughput. This inefficiency is particularly problematic in large-scale deployments where hardware utilization is critical for cost-effectiveness.

Memory access patterns also become less predictable in dynamic models. Standard machine learning models process data in a structured manner, optimizing for efficient memory access. In contrast, dynamic models require frequent branching, leading to irregular memory access and increased latency. Optimizing these models for hardware execution requires specialized scheduling strategies and compiler optimizations to mitigate these inefficiencies, but such solutions add complexity to deployment.

Generalization and Robustness Concerns

Because dynamic computation allows different inputs to take different paths through the model, there is a risk that certain data distributions receive less computation than necessary. If the gating functions are not carefully designed, the model may learn to consistently allocate fewer resources to specific types of inputs, leading to biased predictions. This issue is particularly concerning in safety-critical applications, where failing to allocate enough computation to rare but important inputs can result in catastrophic failures.

Another concern is overfitting to training-time computational paths. If a model is trained with a certain distribution of computational choices, it may struggle to generalize to new inputs where different paths should be taken. Ensuring that a dynamic model remains adaptable to unseen data requires additional robustness mechanisms, such as entropy-based regularization or uncertainty-driven gating, but these introduce additional training complexities.

Dynamic computation also creates new vulnerabilities to adversarial attacks. In standard models, an attacker might attempt to modify an input in a way that alters the final prediction. In dynamic models, an attacker could manipulate the gating mechanisms themselves, forcing the model to choose an incorrect or suboptimal computational path. Defending against such attacks requires additional security measures that further complicate model design and deployment.

Evaluation and Benchmarking Gaps

Most machine learning benchmarks assume a fixed computational budget, making it difficult to evaluate the performance of dynamic models. Traditional metrics such as FLOPs or latency do not fully capture the adaptive nature of these models, where computation varies based on input complexity. As a result, standard benchmarks fail to reflect the true trade-offs between accuracy and efficiency in dynamic architectures.

Another issue is reproducibility. Because dynamic models make input-dependent decisions, running the same model on different hardware or under slightly different conditions can lead to variations in execution paths. This variability complicates fair comparisons between models and requires new evaluation methodologies to accurately assess the benefits of dynamic computation. Without standardized benchmarks that account for adaptive scaling, it remains challenging to measure and compare dynamic models against their static counterparts in a meaningful way.

Despite these challenges, dynamic computation remains a promising direction for optimizing efficiency in machine learning. Addressing these limitations requires more robust training techniques, hardware-aware execution strategies, and improved evaluation frameworks that properly account for dynamic scaling. As machine learning continues to scale and computational constraints become more pressing, solving these challenges will be key to unlocking the full potential of dynamic computation.

10.6.3 Exploiting Sparsity

Sparsity in machine learning refers to the condition where a substantial portion of the elements within a tensor, such as weight matrices or activation tensors, are zero or nearly zero. More formally, for a tensor $T \in \mathbb{R}^{m \times n}$ (or higher dimensions), the sparsity $S$ can be expressed as:

\[ S = \frac{\Vert \mathbf{1}_{\{T_{ij} = 0\}} \Vert_0}{m \times n} \]

where $\mathbf{1}_{\{T_{ij} = 0\}}$ is an indicator function that yields 1 if $T_{ij} = 0$ and 0 otherwise, and $\Vert \cdot \Vert_0$ represents the L0 norm, which counts the number of non-zero elements.

Due to the nature of floating-point representations, we often extend this definition to include elements that are close to zero. This leads to:

\[ S_{\epsilon} = \frac{\Vert \mathbf{1}_{\{|T_{ij}| < \epsilon\}} \Vert_0}{m \times n} \]

where $\epsilon$ is a small threshold value.

Sparsity can emerge naturally during training, often as a result of regularization techniques, or be deliberately introduced through methods like pruning, where elements below a specific threshold are forced to zero. Effectively exploiting sparsity leads to significant computational efficiency, memory savings, and reduced power consumption, which are particularly valuable when deploying models on devices with limited resources, such as mobile phones, embedded systems, and edge devices.

Types of Sparsity

Sparsity in neural networks can be broadly classified into two types: unstructured sparsity and structured sparsity.

Unstructured sparsity occurs when individual weights are set to zero without any specific pattern. This type of sparsity can be achieved through techniques like pruning, where weights that are considered less important (often based on magnitude or other criteria) are removed. While unstructured sparsity is highly flexible and can be applied to any part of the network, it can be less efficient on hardware since it lacks a predictable structure. In practice, exploiting unstructured sparsity requires specialized hardware or software optimizations to make the most of it.

In contrast, structured sparsity involves removing entire components of the network, such as filters, neurons, or channels, in a more systematic manner. By eliminating entire parts of the network, structured sparsity is more efficient on hardware accelerators like GPUs or TPUs, which can leverage this structure for faster computations. Structured sparsity is often used when there is a need for predictability and efficiency in computational resources, as it enables the hardware to fully exploit regular patterns in the network.

Techniques for Exploiting Sparsity

To exploit sparsity effectively in neural networks, several key techniques can be used. These techniques reduce the memory and computational burden of the model while preserving its performance. However, the successful application of these techniques often depends on the availability of specialized hardware support to fully leverage sparsity (Hoefler, Alistarh, Ben-Nun, Dryden, and Peste 2021).

0003, Song Han, Jeff Pool, John Tran, and William J. Dally. 2015. “Learning Both Weights and Connections for Efficient Neural Networks.” CoRR. http://arxiv.org/abs/1506.02626.

Pruning is one of the most widely used methods to introduce sparsity in neural networks. Pruning involves the removal of less important weights or entire components from the network, effectively reducing the number of parameters. This process can be applied in either an unstructured or structured manner. In unstructured pruning, individual weights are removed based on their importance, while structured pruning involves removing entire filters, channels, or layers (0003 et al. 2015). While pruning is highly effective for reducing model size and computation, it requires specialized algorithms and hardware support to fully optimize sparse networks.

Another technique for exploiting sparsity is sparse matrix operations. In sparse matrices, many elements are zero, and these matrices can be stored and processed efficiently, allowing for matrix multiplications with fewer computations. This can be achieved by skipping over the zero elements during the calculation, which significantly reduces the number of arithmetic operations. Specialized hardware, such as GPUs and TPUs, can accelerate these sparse operations by supporting the efficient processing of matrices that contain many zero values (Baraglia and Konno 2019).

For example, consider multiplying a dense 4×4 matrix with a dense vector. In a typical dense implementation, 16 multiplications would be required. However, with sparse-aware implementation, the model only computes the 6 nonzero multiplications, skipping over the zeros. This leads to significant computational savings, especially as the size of the matrix grows.

\[ \begin{bmatrix} 2 & 0 & 0 & 1 \\ 0 & 3 & 0 & 0 \\ 4 & 0 & 5 & 0 \\ 0 & 0 & 0 & 6 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} 2x_1 + x_4 \\ 3x_2 \\ 4x_1 + 5x_3 \\ 6x_4 \end{bmatrix} \]

A third important technique for exploiting sparsity is low-rank approximation. In this approach, large, dense weight matrices are approximated by smaller, lower-rank matrices that capture the most important information while discarding redundant components. This reduces both the storage requirements and computational cost. For instance, a weight matrix of size $1000 \times 1000$ with one million parameters can be factorized into two smaller matrices, say $U$ (size $1000 \times 50$) and $V$ (size $50 \times 1000$), which results in only 100,000 parameters—much fewer than the original one million. This smaller representation retains the key features of the original matrix while significantly reducing the computational burden (Emily Denton 2014).

Emily Denton, Rob Fergus, Soumith Chintala. 2014. “Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation.” In Advances in Neural Information Processing Systems (NeurIPS), 1269–77.

Joulin, Armand, Edouard Grave, Piotr Bojanowski, and Tomas Mikolov. 2017. “Bag of Tricks for Efficient Text Classification.” In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 2, Short Papers, 18:1–42. Association for Computational Linguistics. https://doi.org/10.18653/v1/e17-2068.

Low-rank approximations, such as Singular Value Decomposition, are commonly used to compress weight matrices in neural networks. These approximations are widely applied in recommendation systems and natural language processing models to reduce computational complexity and memory usage without a significant loss in performance (Joulin et al. 2017).

In addition to these core methods, other techniques like sparsity-aware training can also help models to learn sparse representations during training. For instance, using sparse gradient descent, where the training algorithm updates only non-zero elements, can help the model operate with fewer active parameters. While pruning and low-rank approximations directly reduce parameters or factorize weight matrices, sparsity-aware training helps maintain efficient models throughout the training process (Liu et al. 2018).

Liu, C, G Bellec, B Vogginger, D Kappel, J Partzsch, F Neumärker, S Höppner, et al. 2018. “Memory-Efficient Deep Learning on a SpiNNaker 2 Prototype.” Frontiers in Neuroscience 12: 840. https://doi.org/10.3389/fnins.2018.00840.

Hardware Support for Sparsity

Sparsity is a technique for reducing computational cost, memory usage, and power consumption. However, the full potential of sparsity can only be realized when it is supported by hardware designed to efficiently process sparse data and operations. While general-purpose processors like CPUs are capable of handling basic computations, they are not optimized for the specialized tasks that sparse matrix operations require (Han, Mao, and Dally 2016). This limitation can prevent the potential efficiency gains of sparse networks from being fully realized.

———. 2016. “Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding.” International Conference on Learning Representations (ICLR).

Gholami, Amir, Sehoon Kim, Zhen Dong, Zhewei Yao, Michael W. Mahoney, and Kurt Keutzer. 2021b. “A Survey of Quantization Methods for Efficient Neural Network Inference.” arXiv Preprint arXiv:2103.13630, March. http://arxiv.org/abs/2103.13630v3.

To overcome this limitation, hardware accelerators such as GPUs, TPUs, and FPGAs are increasingly used to accelerate sparse network computations. These accelerators are designed with specialized architectures that can exploit sparsity to improve computation speed, memory efficiency, and power usage. In particular, GPUs, TPUs, and FPGAs can handle large-scale matrix operations more efficiently by skipping over zero elements in sparse matrices, leading to significant reductions in both computational cost and memory bandwidth usage (Gholami et al. 2021b).

The role of hardware support for sparsity is integral to the broader goal of model optimization. While sparsity techniques—such as pruning and low-rank approximation—serve to simplify and compress neural networks, hardware accelerators ensure that these optimizations lead to actual performance gains during training and inference. Therefore, hardware considerations are a critical component of model optimization, as specialized accelerators are necessary to efficiently process sparse data and achieve the desired reductions in both computation time and resource consumption.

GPUs and Sparse Operations

Graphics Processing Units (GPUs) are widely recognized for their ability to perform highly parallel computations, making them ideal for handling the large-scale matrix operations that are common in machine learning. Modern GPUs, such as NVIDIA’s Ampere architecture, include specialized Sparse Tensor Cores that accelerate sparse matrix multiplications. These tensor cores are designed to recognize and skip over zero elements in sparse matrices, thereby reducing the number of operations required (Abdelkhalik et al. 2022). This is particularly advantageous for structured pruning techniques, where entire filters, channels, or layers are pruned, resulting in a significant reduction in the amount of computation. By skipping over the zero values, GPUs can speed up matrix multiplications by a factor of two or more, resulting in lower processing times and reduced power consumption for sparse networks.

Abdelkhalik, Hamdy, Yehia Arafa, Nandakishore Santhi, and Abdel-Hameed A. Badawy. 2022. “Demystifying the Nvidia Ampere Architecture Through Microbenchmarking and Instruction-Level Analysis.” In 2022 IEEE High Performance Extreme Computing Conference (HPEC). IEEE. https://doi.org/10.1109/hpec55821.2022.9926299.

Hoefler, Torsten, Dan Alistarh, Tal Ben-Nun, Nikoli Dryden, and Alexandra Peste. 2021. “Sparsity in Deep Learning: Pruning and Growth for Efficient Inference and Training in Neural Networks.” arXiv Preprint arXiv:2102.00554 22 (January): 1–124. http://arxiv.org/abs/2102.00554v1.

Furthermore, GPUs leverage their parallel architecture to handle multiple operations simultaneously. This parallelism is especially beneficial for sparse operations, as it allows the hardware to exploit the inherent sparsity in the data more efficiently. However, the full benefit of sparse operations on GPUs requires that the sparsity is structured in a way that aligns with the underlying hardware architecture, making structured pruning more advantageous for optimization (Hoefler, Alistarh, Ben-Nun, Dryden, and Peste 2021).

TPUs and Sparse Matrix Optimization

TPUs, developed by Google, are custom-built hardware accelerators specifically designed to handle tensor computations at a much higher efficiency than traditional processors. TPUs, such as TPU v4, have built-in support for sparse weight matrices, which is particularly beneficial for models like transformers, including BERT and GPT, that rely on large-scale matrix multiplications (Jouppi et al. 2021). TPUs optimize sparse weight matrices by reducing the computational load associated with zero elements, enabling faster processing and improved energy efficiency.

Jouppi, Norman P., Doe Hyun Yoon, Matthew Ashcraft, Mark Gottscho, Thomas B. Jablin, George Kurian, James Laudon, et al. 2021. “Ten Lessons from Three Generations Shaped Google’s TPUv4i : Industrial Product.” In 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), 1–14. IEEE. https://doi.org/10.1109/isca52012.2021.00010.

The efficiency of TPUs comes from their ability to perform operations at high throughput and low latency, thanks to their custom-designed matrix multiply units. These units are able to accelerate sparse matrix operations by directly processing the non-zero elements, making them well-suited for models that incorporate significant sparsity, whether through pruning or low-rank approximations. As the demand for larger models increases, TPUs continue to play a critical role in maintaining performance while minimizing the energy and computational cost associated with dense computations.

FPGAs and Custom Sparse Computations

Field-Programmable Gate Arrays (FPGAs) are another important class of hardware accelerators for sparse networks. Unlike GPUs and TPUs, FPGAs are highly customizable, offering flexibility in their design to optimize specific computational tasks. This makes them particularly suitable for sparse operations that require fine-grained control over hardware execution. FPGAs can be programmed to perform sparse matrix-vector multiplications and other sparse matrix operations with minimal overhead, delivering high performance for models that use unstructured pruning or require custom sparse patterns.

One of the main advantages of FPGAs in sparse networks is their ability to be tailored for specific applications, which allows for optimizations that general-purpose hardware cannot achieve. For instance, an FPGA can be designed to skip over zero elements in a matrix by customizing the data path and memory management, providing significant savings in both computation and memory usage. FPGAs also allow for low-latency execution, making them well-suited for real-time applications that require efficient processing of sparse data streams.

Memory and Energy Optimization

One of the key challenges in sparse networks is managing memory bandwidth, as matrix operations often require significant memory access. Sparse networks offer a solution by reducing the number of elements that need to be accessed, thus minimizing memory traffic. Hardware accelerators are optimized for these sparse matrices, utilizing specialized memory access patterns that skip zero values, reducing the total amount of memory bandwidth used (Baraglia and Konno 2019).

Baraglia, David, and Hokuto Konno. 2019. “On the Bauer-Furuta and Seiberg-Witten Invariants of Families of $4$-Manifolds.” arXiv Preprint arXiv:1903.01649, March, 8955–67. http://arxiv.org/abs/1903.01649v3.

For example, GPUs and TPUs are designed to minimize memory access latency by taking advantage of their high memory bandwidth. By accessing only non-zero elements, these accelerators ensure that memory is used more efficiently. The memory hierarchies in these devices are also optimized for sparse computations, allowing for faster data retrieval and reduced power consumption.

The reduction in the number of computations and memory accesses directly translates into energy savings. Sparse operations require fewer arithmetic operations and fewer memory fetches, leading to a decrease in the energy consumption required for both training and inference. This energy efficiency is particularly important for applications that run on edge devices, where power constraints are critical. Hardware accelerators like TPUs and GPUs are optimized to handle these operations efficiently, making sparse networks not only faster but also more energy-efficient (Cheng 2022).

Cheng, Yu et al. 2022. “Memory-Efficient Deep Learning: Advances in Model Compression and Sparsification.” ACM Computing Surveys.

Looking Ahead: Hardware and Sparse Networks

As hardware continues to evolve, we can expect more innovations tailored specifically for sparse networks. Future hardware accelerators may offer deeper integration with sparsity-aware training and optimization algorithms, allowing even greater reductions in computational and memory costs. Emerging fields like neuromorphic computing, inspired by the brain’s structure, may provide new avenues for processing sparse networks in energy-efficient ways (Davies 2021). These advancements promise to further enhance the efficiency and scalability of machine learning models, particularly in applications that require real-time processing and run on power-constrained devices.

Davies, Mike et al. 2021. “Advancing Neuromorphic Computing with Sparse Networks.” Nature Electronics.

Challenges and Limitations of Sparsity

While exploiting sparsity offers significant advantages in reducing computational cost and memory usage, several challenges and limitations must be considered for the effective implementation of sparse networks. Table Table 10.10 summarizes some of the challenges and limitations associated with sparsity optimizations.

Table 10.10: Challenges and limitations of sparsity optimization for architectural efficiency.

Challenge	Description	Impact
Unstructured Sparsity Optimization	Irregular sparse patterns make it difficult to exploit sparsity on hardware.	Limited hardware acceleration and reduced computational savings.
Algorithmic Complexity	Sophisticated pruning and sparse matrix operations require complex algorithms.	High computational overhead and algorithmic complexity for large models.
Hardware Support	Hardware accelerators are optimized for structured sparsity, making unstructured sparsity harder to optimize.	Suboptimal hardware utilization and lower performance for unstructured sparsity.
Accuracy Trade-off	Aggressive sparsity may degrade model accuracy if not carefully balanced.	Potential loss in performance, requiring careful tuning and validation.
Energy Efficiency	Overhead from sparse matrix storage and management can offset the energy savings from reduced computation.	Power consumption may not improve if the overhead surpasses savings from sparse computations.
Limited Applicability	Sparsity may not benefit all models or tasks, especially in domains requiring dense representations.	Not all models or hardware benefit equally from sparsity.

One of the main challenges of sparsity is the optimization of unstructured sparsity. In unstructured pruning, individual weights are removed based on their importance, leading to an irregular sparse pattern. This irregularity makes it difficult to fully exploit the sparsity on hardware, as most hardware accelerators (like GPUs and TPUs) are designed to work more efficiently with structured data. Without a regular structure, these accelerators may not be able to skip zero elements as effectively, which can limit the computational savings.

Another challenge is the algorithmic complexity involved in pruning and sparse matrix operations. The process of deciding which weights to prune, particularly in an unstructured manner, requires sophisticated algorithms that must balance model accuracy with computational efficiency. These pruning algorithms can be computationally expensive themselves, and applying them across large models can result in significant overhead. The optimization of sparse matrices also requires specialized techniques that may not always be easy to implement or generalize across different architectures.

Hardware support is another important limitation. Although modern GPUs, TPUs, and FPGAs have specialized features designed to accelerate sparse operations, fully optimizing sparse networks on hardware requires careful alignment between the hardware architecture and the sparsity format. While structured sparsity is easier to leverage on these accelerators, unstructured sparsity remains a challenge, as hardware accelerators may struggle to efficiently handle irregular sparse patterns. Even when hardware is optimized for sparse operations, the overhead associated with sparse matrix storage formats and the need for specialized memory management can still result in suboptimal performance.

Moreover, there is always a trade-off between sparsity and accuracy. Aggressive pruning or low-rank approximation techniques that aggressively reduce the number of parameters can lead to accuracy degradation. Finding the right balance between reducing parameters and maintaining high model performance is a delicate process that requires extensive experimentation. In some cases, introducing too much sparsity can result in a model that is too small or too underfit to achieve high performance.

Additionally, while sparsity can lead to energy savings, energy efficiency is not always guaranteed. Although sparse operations require fewer floating-point operations, the overhead of managing sparse data and ensuring that hardware optimally skips over zero values can introduce additional power consumption. In edge devices or mobile environments with tight power budgets, the benefits of sparsity may be less clear if the overhead associated with sparse data structures and hardware utilization outweighs the energy savings.

Finally, there is a limited applicability of sparsity to certain types of models or tasks. Not all models benefit equally from sparsity, especially those where dense representations are crucial for performance. For example, models in domains such as image segmentation or some types of reinforcement learning may not show significant gains when sparsity is introduced. Additionally, sparsity may not be effective for all hardware platforms, particularly for older or lower-end devices that lack the computational power or specialized features required to take advantage of sparse matrix operations.

Sparsity and Its Interaction with Other Optimizations

While sparsity in neural networks is a powerful technique for improving computational efficiency and reducing memory usage, its full potential is often realized when it is used alongside other optimization strategies. These optimizations include techniques like pruning, quantization, and efficient model design. Understanding how sparsity interacts with these methods is crucial for effectively combining them to achieve optimal performance (Hoefler, Alistarh, Ben-Nun, Dryden, and Ziogas 2021).

Hoefler, Torsten, Dan Alistarh, Tal Ben-Nun, Nikoli Dryden, and Alexandros Nikolaos Ziogas. 2021. “Sparsity in Deep Learning: Pruning and Growth for Efficient Inference and Training in Neural Networks.” Journal of Machine Learning Research 22 (241): 1–124.

Sparsity and Pruning

Pruning and sparsity are closely related techniques. Pruning is the process of removing unimportant weights or entire components from a network, typically resulting in a sparse model. The goal of pruning is to reduce the number of parameters and operations required during inference, and it inherently leads to sparsity in the model. However, the interaction between pruning and sparsity is not always straightforward.

When pruning is applied, the resulting model may become sparse, but the sparsity pattern—whether structured or unstructured—affects how effectively the model can be optimized for hardware. For example, structured pruning (e.g., pruning entire filters or layers) typically results in more efficient sparsity, as hardware accelerators like GPUs and TPUs are better equipped to handle regular patterns in sparse matrices (Elsen et al. 2020). Unstructured pruning, on the other hand, can introduce irregular sparsity patterns, which may not be as efficiently processed by hardware, especially when combined with other techniques like quantization.

Pruning methods often rely on the principle of removing weights that have little impact on the model’s performance, but when combined with sparsity, they require careful coordination with hardware-specific optimizations. For instance, sparse patterns created by pruning need to align with the underlying hardware architecture to achieve the desired computational savings (Gale, Elsen, and Hooker 2019b).

Sparsity and Quantization

Quantization is another optimization technique that reduces the precision of the model’s weights, typically converting them from floating-point numbers to lower-precision integers. When sparsity and quantization are used together, they can complement each other by further reducing the memory footprint and computational cost.

However, the interaction between sparsity and quantization presents unique challenges. While sparsity reduces the number of non-zero elements in a model, quantization reduces the precision of the individual weights. When these two optimizations are applied together, they can lead to significant reductions in both memory usage and computation, but also pose trade-offs in model accuracy (Nagel et al. 2021b). If the sparsity is unstructured, it may exacerbate the challenges of processing the low-precision weights effectively, especially if the hardware does not support irregular sparse matrices efficiently.

Nagel, Markus, Marios Fournarakis, Rana Ali Amjad, Yelysei Bondarenko, Mart van Baalen, and Tijmen Blankevoort. 2021b. “A White Paper on Neural Network Quantization.” arXiv Preprint arXiv:2106.08295, June. http://arxiv.org/abs/2106.08295v1.

Zhang, Yi, Jianlei Yang, Linghao Song, Yiyu Shi, Yu Wang, and Yuan Xie. 2021. “Learning-Based Efficient Sparsity and Quantization for Neural Network Compression.” IEEE Transactions on Neural Networks and Learning Systems 32 (9): 3980–94.

Moreover, both sparsity and quantization require hardware that is specifically optimized for these operations. For instance, GPUs and TPUs can accelerate sparse matrix operations, but these gains are amplified when combined with low-precision arithmetic operations. In contrast, CPUs may struggle with the combined overhead of managing sparse and low-precision data simultaneously (Zhang et al. 2021).

Sparsity and Efficient Model Design

Efficient model design focuses on creating architectures that are inherently efficient, without the need for extensive post-training optimizations like pruning or quantization. Techniques like depthwise separable convolutions, low-rank approximation, and dynamic computation contribute to sparsity indirectly by reducing the number of parameters or the computational complexity required by a network.

Sparsity enhances the impact of efficient design by reducing the memory and computation requirements even further. For example, using low-rank approximations to compress weight matrices can result in fewer parameters and reduced model size, while sparsity ensures that these smaller models are processed efficiently (Dettmers and Zettlemoyer 2019). Additionally, when applied to models designed with efficient structures, sparsity ensures that the reduction in operations is fully realized during both training and inference.

Dettmers, Tim, and Luke Zettlemoyer. 2019. “Sparse Networks from Scratch: Faster Training Without Losing Performance.” arXiv Preprint arXiv:1907.04840, July. http://arxiv.org/abs/1907.04840v2.

Elsen, Erich, Marat Dukhan, Trevor Gale, and Karen Simonyan. 2020. “Fast Sparse ConvNets.” In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 14617–26. IEEE. https://doi.org/10.1109/cvpr42600.2020.01464.

However, a model designed for efficiency that incorporates sparsity must also be optimized for hardware that supports sparse operations. Without specialized hardware support for sparse data, even the most efficient models can experience suboptimal performance. Therefore, efficient design and sparsity must be aligned with the underlying hardware to ensure that both computational cost and memory usage are minimized (Elsen et al. 2020).

Challenges of Combining Sparsity with Other Optimizations

While sparsity can provide significant benefits when combined with pruning, quantization, and efficient model design, there are also challenges in coordinating these techniques. One major challenge is that each optimization method introduces its own set of trade-offs, particularly when it comes to model accuracy. Sparsity can lead to loss of information, while quantization can reduce the precision of the weights, both of which can negatively impact performance if not carefully tuned. Similarly, pruning can result in overly aggressive reductions that degrade accuracy if not managed properly (Labarge, n.d.).

Labarge, Isaac E. n.d. “Neural Network Pruning for ECG Arrhythmia Classification.” Proceedings of Machine Learning and Systems (MLSys). PhD thesis, California Polytechnic State University. https://doi.org/10.15368/theses.2020.76.

Gale, Trevor, Erich Elsen, and Sara Hooker. 2019b. “The State of Sparsity in Deep Neural Networks.” arXiv Preprint arXiv:1902.09574, February. http://arxiv.org/abs/1902.09574v1.

Furthermore, hardware support is a key factor in determining how well these techniques work together. For example, sparsity is more effective when it is structured in a way that aligns with the architecture of the hardware. Hardware accelerators like GPUs and TPUs are optimized for structured sparsity, but may struggle with unstructured patterns or combinations of sparsity and quantization. Achieving optimal performance requires selecting the right combination of sparsity, quantization, pruning, and efficient design, as well as ensuring that the model is aligned with the capabilities of the hardware (Gale, Elsen, and Hooker 2019b).

In summary, sparsity interacts closely with pruning, quantization, and efficient model design. While each of these techniques has its own strengths, combining them requires careful consideration of their impact on model accuracy, computational cost, memory usage, and hardware efficiency. When applied together, these optimizations can lead to significant reductions in both computation and memory usage, but their effectiveness depends on how well they are coordinated and aligned with hardware capabilities. By understanding the synergies and trade-offs between sparsity and other optimization techniques, practitioners can design more efficient models that are well-suited for deployment in real-world, resource-constrained environments.

10.7 AutoML: A Holistic Approach to Model Optimization

As machine learning models grow in complexity, optimizing them for real-world deployment requires balancing multiple factors, including accuracy, efficiency, and hardware constraints. In this chapter, we have explored various optimization techniques—such as pruning, quantization, and neural architecture search—each of which targets specific aspects of model efficiency. However, applying these optimizations effectively often requires extensive manual effort, domain expertise, and iterative experimentation.

Automated Machine Learning (AutoML) aims to streamline this process by automating the search for optimal model configurations. AutoML frameworks leverage machine learning algorithms to optimize architectures, hyperparameters, model compression techniques, and other critical parameters, reducing the need for human intervention (Hutter, Kotthoff, and Vanschoren 2019). By systematically exploring the vast design space of possible models, AutoML can improve efficiency while maintaining competitive accuracy, often discovering novel solutions that may be overlooked through manual tuning (Zoph and Le 2017b).

Hutter, Frank, Lars Kotthoff, and Joaquin Vanschoren. 2019. Automated Machine Learning: Methods, Systems, Challenges. Springer International Publishing. https://doi.org/10.1007/978-3-030-05318-5.

AutoML does not replace the need for human expertise but rather enhances it by providing a systematic and scalable approach to model optimization. Instead of manually adjusting pruning thresholds, quantization strategies, or architecture designs, practitioners can define high-level objectives—such as latency constraints, memory limits, or accuracy targets—and allow AutoML systems to explore configurations that best satisfy these constraints (Feurer et al. 2019).

We will explore the core aspects of AutoML, starting with the key dimensions of optimization, followed by the methodologies used in AutoML systems, and concluding with challenges and limitations. By the end, we will understand how AutoML serves as an integrative framework that unifies many of the optimization strategies discussed earlier in this chapter.

10.7.1 AutoML Optimizations

AutoML is designed to optimize multiple aspects of a machine learning model, ensuring efficiency, accuracy, and deployability. Unlike traditional approaches that focus on individual techniques, such as quantization for reducing numerical precision or pruning for compressing models, AutoML takes a holistic approach by jointly considering these factors. This enables a more comprehensive search for optimal model configurations, balancing performance with real-world constraints (He et al. 2018).

He, Yihui, Ji Lin, Zhijian Liu, Hanrui Wang, Li-Jia Li, and Song Han. 2018. “AMC: AutoML for Model Compression and Acceleration on Mobile Devices.” In Computer Vision – ECCV 2018, 815–32. Springer International Publishing. https://doi.org/10.1007/978-3-030-01234-2\_48.

Elsken, Thomas, Jan Hendrik Metzen, and Frank Hutter. 2019b. “Neural Architecture Search.” In Automated Machine Learning, 63–77. Springer International Publishing. https://doi.org/10.1007/978-3-030-05318-5\_3.

Tan, Mingxing, and Quoc V. Le. 2019b. “EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks.” In International Conference on Machine Learning.

One of the primary optimization targets of AutoML is neural network architecture search. Designing an efficient model architecture is a complex process that requires balancing layer configurations, connectivity patterns, and computational costs. NAS automates this by systematically exploring different network structures, evaluating their efficiency, and selecting the most optimal design (Elsken, Metzen, and Hutter 2019b). This process has led to the discovery of architectures such as MobileNetV3 and EfficientNet, which outperform manually designed models on key efficiency metrics (Tan and Le 2019b).

Beyond architecture design, AutoML also focuses on hyperparameter optimization, which plays a crucial role in determining a model’s performance. Parameters such as learning rate, batch size, weight decay, and activation functions must be carefully tuned for stability and efficiency. Instead of relying on trial and error, AutoML frameworks employ systematic search strategies, including Bayesian optimization, evolutionary algorithms, and adaptive heuristics, to efficiently identify the best hyperparameter settings for a given model and dataset (Bardenet et al. 2015).

Bardenet, Rémi, Olivier Cappé, Gersende Fort, and Balázs Kégl. 2015. “Adaptive MCMC with Online Relabeling.” Bernoulli 21 (3). https://doi.org/10.3150/13-bej578.

Wu, Jiaxiang, Cong Leng, Yuhang Wang, Qinghao Hu, and Jian Cheng. 2016. “Quantized Convolutional Neural Networks for Mobile Devices.” In 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 4820–28. IEEE. https://doi.org/10.1109/cvpr.2016.521.

Chowdhery, Aakanksha, Anatoli Noy, Gaurav Misra, Zhuyun Dai, Quoc V. Le, and Jeff Dean. 2021. “Edge TPU: An Edge-Optimized Inference Accelerator for Deep Learning.” In International Symposium on Computer Architecture.

Another critical aspect of AutoML is model compression. Techniques such as pruning and quantization help reduce the memory footprint and computational requirements of a model, making it more suitable for deployment on resource-constrained hardware. AutoML frameworks automate the selection of pruning thresholds, sparsity patterns, and quantization levels, optimizing models for both speed and energy efficiency (Jiaxiang Wu et al. 2016). This is particularly important for edge AI applications, where models need to operate with minimal latency and power consumption (Chowdhery et al. 2021).

Finally, AutoML considers deployment-aware optimization, ensuring that the final model is suited for real-world execution. Different hardware platforms impose varying constraints on model execution, such as memory bandwidth limitations, computational throughput, and energy efficiency requirements. AutoML frameworks incorporate hardware-aware optimization techniques, tailoring models to specific devices by adjusting computational workloads, memory access patterns, and execution strategies (Cai, Gan, and Han 2020).

Cai, Han, Chuang Gan, and Song Han. 2020. “Once-for-All: Train One Network and Specialize It for Efficient Deployment.” In International Conference on Learning Representations.

Optimization across these dimensions enables AutoML to provide a unified framework for enhancing machine learning models, streamlining the process to achieve efficiency without sacrificing accuracy. This holistic approach ensures that models are not only theoretically optimal but also practical for real-world deployment across diverse applications and hardware platforms.

10.7.2 Optimization Strategies

AutoML systems optimize machine learning models by systematically exploring different configurations and selecting the most efficient combination of architectures, hyperparameters, and compression strategies. Unlike traditional manual tuning, which requires extensive domain expertise and iterative experimentation, AutoML leverages algorithmic search methods to automate this process. The effectiveness of AutoML depends on how it navigates the vast design space of possible models while balancing accuracy, efficiency, and deployment constraints.

The foundation of AutoML lies in search-based optimization strategies that efficiently explore different configurations. One of the most well-known techniques within AutoML is NAS, which automates the design of machine learning models. NAS frameworks employ methods such as reinforcement learning, evolutionary algorithms, and gradient-based optimization to discover architectures that maximize efficiency while maintaining high accuracy (Zoph and Le 2017b). By systematically evaluating candidate architectures, NAS can identify structures that outperform manually designed models, leading to breakthroughs in efficient machine learning (Real et al. 2019b).

Zoph, Barret, and Quoc V. Le. 2017b. “Neural Architecture Search with Reinforcement Learning.” In International Conference on Learning Representations.

Real, Esteban, Alok Aggarwal, Yanping Huang, and Quoc V. Le. 2019b. “Regularized Evolution for Image Classifier Architecture Search.” Proceedings of the AAAI Conference on Artificial Intelligence 33 (01): 4780–89. https://doi.org/10.1609/aaai.v33i01.33014780.

Feurer, Matthias, Aaron Klein, Katharina Eggensperger, Jost Tobias Springenberg, Manuel Blum, and Frank Hutter. 2019. “Auto-Sklearn: Efficient and Robust Automated Machine Learning.” In Automated Machine Learning, 113–34. Springer International Publishing. https://doi.org/10.1007/978-3-030-05318-5\_6.

Beyond architecture search, AutoML systems also focus on hyperparameter optimization (HPO), which fine-tunes crucial training parameters such as learning rate, batch size, and weight decay. Instead of relying on grid search or manual tuning, AutoML frameworks employ Bayesian optimization, random search, and adaptive heuristics to efficiently identify the best hyperparameter settings (Feurer et al. 2019). These methods allow AutoML to converge on optimal configurations faster than traditional trial-and-error approaches.

Another key aspect of AutoML is model compression optimization, where pruning and quantization strategies are automatically selected based on deployment requirements. By evaluating trade-offs between model size, latency, and accuracy, AutoML frameworks determine the best way to reduce computational costs while preserving performance. This enables efficient model deployment on resource-constrained devices without extensive manual tuning.

In addition to optimizing model structures and hyperparameters, AutoML also incorporates data processing and augmentation strategies. Training data quality is critical for achieving high model performance, and AutoML frameworks can automatically determine the best preprocessing techniques to enhance generalization. Techniques such as automated feature selection, adaptive augmentation policies, and dataset balancing are employed to improve model robustness without introducing unnecessary computational overhead.

Recent advancements in AutoML have also led to meta-learning approaches, where knowledge from previous optimization tasks is leveraged to accelerate the search for new models. By learning from prior experiments, AutoML systems can intelligently navigate the optimization space, reducing the computational cost associated with training and evaluation (Vanschoren 2018). This allows for faster adaptation to new tasks and datasets.

Vanschoren, Joaquin. 2018. “Meta-Learning: A Survey.” ArXiv Preprint arXiv:1810.03548, October. http://arxiv.org/abs/1810.03548v1.

Li, Lisha, Kevin G. Jamieson, Giulia DeSalvo, Afshin Rostamizadeh, and Ameet Talwalkar. 2017. “Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization.” J. Mach. Learn. Res. 18: 185:1–52. https://jmlr.org/papers/v18/16-558.html.

Finally, many modern AutoML frameworks offer end-to-end automation, integrating architecture search, hyperparameter tuning, and model compression into a single pipeline. Platforms such as Google AutoML, Amazon SageMaker Autopilot, and Microsoft Azure AutoML provide fully automated workflows that streamline the entire model optimization process (L. Li et al. 2017).

The integration of these strategies enables AutoML systems to provide a scalable and efficient approach to model optimization, reducing the reliance on manual experimentation. This automation not only accelerates model development but also enables the discovery of novel architectures and configurations that might otherwise be overlooked.

10.7.3 Challenges and Considerations

While AutoML offers a powerful framework for optimizing machine learning models, it also introduces several challenges and trade-offs that must be carefully considered. Despite its ability to automate model design and hyperparameter tuning, AutoML is not a one-size-fits-all solution. The effectiveness of AutoML depends on computational resources, dataset characteristics, and the specific constraints of a given application.

One of the most significant challenges in AutoML is computational cost. The process of searching for optimal architectures, hyperparameters, and compression strategies requires evaluating numerous candidate models, each of which must be trained and validated. Methods like NAS can be particularly expensive, often requiring thousands of GPU hours to explore a large search space. While techniques such as early stopping, weight sharing, and surrogate models help reduce search costs, the computational overhead remains a major limitation, especially for organizations with limited access to high-performance computing resources.

Another challenge is bias in search strategies, which can influence the final model selection. The optimization process in AutoML is guided by heuristics and predefined objectives, which may lead to biased results depending on how the search space is defined. If the search algorithm prioritizes certain architectures or hyperparameters over others, it may fail to discover alternative configurations that could be more effective for specific tasks. Additionally, biases in training data can propagate through the AutoML process, reinforcing unwanted patterns in the final model.

Generalization and transferability present additional concerns. AutoML-generated models are optimized for specific datasets and deployment conditions, but their performance may degrade when applied to new tasks or environments. Unlike manually designed models, where human intuition can guide the selection of architectures that generalize well, AutoML relies on empirical evaluation within a constrained search space. This limitation raises questions about the robustness of AutoML-optimized models when faced with real-world variability.

Interpretability is another key consideration. Many AutoML-generated architectures and configurations are optimized for efficiency but lack transparency in their design choices. Understanding why a particular AutoML-discovered model performs well can be challenging, making it difficult for practitioners to debug issues or adapt models for specific needs. The black-box nature of some AutoML techniques limits human insight into the underlying optimization process.

Beyond technical challenges, there is also a trade-off between automation and control. While AutoML reduces the need for manual intervention, it also abstracts away many decision-making processes that experts might otherwise fine-tune for specific applications. In some cases, domain knowledge is essential for guiding model optimization, and fully automated systems may not always account for subtle but important constraints imposed by the problem domain.

Despite these challenges, AutoML continues to evolve, with ongoing research focused on reducing computational costs, improving generalization, and enhancing interpretability. As these improvements emerge, AutoML is expected to play an increasingly prominent role in the development of optimized machine learning models, making AI systems more accessible and efficient for a wide range of applications.

10.8 Software and Framework Support

The theoretical understanding of model optimization techniques like pruning, quantization, and efficient numerics is essential, but their practical implementation relies heavily on robust software support. Without extensive framework development and tooling, these optimization methods would remain largely inaccessible to practitioners. For instance, implementing quantization would require manual modification of model definitions and careful insertion of quantization operations throughout the network. Similarly, pruning would involve direct manipulation of weight tensors—tasks that become prohibitively complex as models scale.

The widespread adoption of model optimization techniques has been enabled by significant advances in software frameworks, optimization tools, and hardware integration. Modern machine learning frameworks provide high-level APIs and automated workflows that abstract away much of the complexity involved in applying these optimizations. This software infrastructure makes sophisticated optimization techniques accessible to a broader audience of practitioners, enabling the deployment of efficient models across diverse applications.

Framework support addresses several critical challenges in model optimization:

Implementation Complexity: Frameworks provide pre-built modules and functions for common optimization techniques, eliminating the need for custom implementations.
Hyperparameter Management: Tools assist in tuning optimization parameters, such as pruning schedules or quantization bit-widths.
Performance Trade-offs: Software helps manage the balance between model compression and accuracy through automated evaluation pipelines.
Hardware Compatibility: Frameworks ensure optimized models remain compatible with target deployment platforms through device-specific code generation and validation.

The support provided by frameworks transforms the theoretical optimization techniques we learned into practical tools that can be readily applied in production environments. This accessibility has been crucial in bridging the gap between academic research and industrial applications, enabling the widespread deployment of efficient machine learning models.

10.8.1 Built-in Optimization APIs

Modern machine learning frameworks provide extensive APIs and libraries that enable practitioners to apply optimization techniques without implementing complex algorithms from scratch. These built-in optimizations enhance model efficiency while ensuring adherence to established best practices. Leading frameworks such as TensorFlow, PyTorch, and MXNet offer comprehensive toolkits for model optimization, streamlining the deployment of efficient machine learning systems.

TensorFlow provides robust optimization capabilities through its Model Optimization Toolkit, which facilitates various techniques, including quantization, pruning, and clustering. QAT within the toolkit enables the conversion of floating-point models to lower-precision formats, such as INT8, while preserving model accuracy. The toolkit systematically manages both weight and activation quantization, ensuring consistency across diverse model architectures.

Beyond quantization, TensorFlow’s optimization suite includes pruning algorithms that introduce sparsity into neural networks by removing redundant connections at different levels of granularity, from individual weights to entire layers. This flexibility allows practitioners to tailor pruning strategies to their specific requirements. Additionally, weight clustering groups similar weights together to achieve model compression while preserving core functionality. By leveraging these optimization techniques, TensorFlow provides multiple pathways for improving model efficiency beyond traditional quantization.

Similarly, PyTorch offers comprehensive optimization support through built-in modules for quantization and pruning. The torch.quantization package provides tools for converting models to lower-precision representations, supporting both post-training quantization (PTQ) and quantization-aware training (QAT):

import torch
from torch.quantization import QuantStub, DeQuantStub, prepare_qat

# Define a model with quantization support
class QuantizedModel(torch.nn.Module):
    def __init__(self):
        super().__init__()
        self.quant = QuantStub()
        self.conv = torch.nn.Conv2d(3, 64, 3)
        self.dequant = DeQuantStub()

    def forward(self, x):
        x = self.quant(x)
        x = self.conv(x)
        return self.dequant(x)

# Prepare model for quantization-aware training
model = QuantizedModel()
model.qconfig = torch.quantization.get_default_qat_qconfig()
model_prepared = prepare_qat(model)

For pruning, PyTorch provides the torch.nn.utils.prune module, which supports both unstructured and structured pruning:

import torch.nn.utils.prune as prune

# Apply unstructured pruning
module = torch.nn.Linear(10, 10)
prune.l1_unstructured(module, name='weight', amount=0.3)  # Prune 30% of weights

# Apply structured pruning
prune.ln_structured(module, name='weight', amount=0.5, n=2, dim=0)

These tools integrate seamlessly into PyTorch’s training pipelines, enabling efficient experimentation with different optimization strategies.

Built-in optimization APIs offer substantial benefits that make model optimization more accessible and reliable. By providing pre-tested, production-ready tools, these APIs dramatically reduce the implementation complexity that practitioners face when optimizing their models. Rather than having to implement complex optimization algorithms from scratch, developers can leverage standardized interfaces that have been thoroughly vetted.

The consistency provided by these built-in APIs is particularly valuable when working across different model architectures. The standardized interfaces ensure that optimization techniques are applied uniformly, reducing the risk of implementation errors or inconsistencies that could arise from custom solutions. This standardization helps maintain reliable and reproducible results across different projects and teams.

These frameworks also serve as a bridge between cutting-edge research and practical applications. As new optimization techniques emerge from the research community, framework maintainers incorporate these advances into their APIs, making state-of-the-art methods readily available to practitioners. This continuous integration of research advances ensures that developers have access to the latest optimization strategies without needing to implement them independently.

Furthermore, the comprehensive nature of built-in APIs enables rapid experimentation with different optimization approaches. Developers can easily test various strategies, compare their effectiveness, and iterate quickly to find the optimal configuration for their specific use case. This ability to experiment efficiently is crucial for finding the right balance between model performance and resource constraints.

As model optimization continues to evolve, major frameworks maintain and expand their built-in support, further reducing barriers to efficient model deployment. The standardization of these APIs has played a crucial role in democratizing access to model efficiency techniques while ensuring high-quality implementations remain consistent and reliable.

10.8.2 Hardware Optimization Libraries

Hardware optimization libraries in modern machine learning frameworks enable efficient deployment of optimized models across different hardware platforms. These libraries integrate directly with training and deployment pipelines to provide hardware-specific acceleration for various optimization techniques across model representation, numerical precision, and architectural efficiency dimensions.

For model representation optimizations like pruning, libraries such as TensorRT, XLA, and OpenVINO provide sparsity-aware acceleration through optimized kernels that efficiently handle sparse computations. TensorRT specifically supports structured sparsity patterns, allowing models trained with techniques like two-out-of-four structured pruning to run efficiently on NVIDIA GPUs. Similarly, TPUs leverage XLA’s sparse matrix optimizations, while FPGAs enable custom sparse execution through frameworks like Vitis AI.

Knowledge distillation benefits from hardware-aware optimizations that help compact student models achieve high inference efficiency. Libraries like TensorRT, OpenVINO, and SNPE optimize distilled models for low-power execution, often combining distillation with quantization or architectural restructuring to meet hardware constraints. For models discovered through neural architecture search (NAS), frameworks such as TVM and TIMM provide compiler support to tune the architectures for various hardware backends.

In terms of numerical precision optimization, these libraries offer extensive support for both PTQ and QAT. TensorRT and TensorFlow Lite implement INT8 and INT4 quantization during model conversion, reducing computational complexity while leveraging specialized hardware acceleration on mobile SoCs and edge AI chips. NVIDIA TensorRT incorporates calibration-based quantization using representative datasets to optimize weight and activation scaling.

More granular quantization approaches like channelwise and groupwise quantization are supported in frameworks such as SNPE and OpenVINO. Dynamic quantization capabilities in PyTorch and ONNX Runtime enable runtime activation quantization, making models adaptable to varying hardware conditions. For extreme precision reduction, techniques like binarization and ternarization are optimized through libraries such as CMSIS-NN, enabling efficient execution of binary-weight models on ARM Cortex-M microcontrollers.

Architectural efficiency techniques integrate tightly with hardware-specific execution frameworks. TensorFlow XLA and TVM provide operator-level tuning through aggressive fusion and kernel reordering, improving efficiency across GPUs, TPUs, and edge devices. Dynamic computation approaches like early exit architectures and conditional computation are supported by custom execution runtimes that optimize control flow.

The widespread support for sparsity-aware execution spans multiple hardware platforms. NVIDIA GPUs utilize specialized sparse tensor cores for accelerating structured sparse models, while TPUs implement hardware-level sparse matrix optimizations. On FPGAs, vendor-specific compilers like Vitis AI enable custom sparse computations to be highly optimized.

This comprehensive integration of hardware optimization libraries with machine learning frameworks enables developers to effectively implement pruning, quantization, NAS, dynamic computation, and sparsity-aware execution while ensuring optimal adaptation to target hardware. The ability to optimize across multiple dimensions—from model representation to numerical precision and architectural efficiency—is crucial for deploying machine learning models efficiently across diverse platforms.

10.8.3 Visualizing Optimizations

Model optimization techniques fundamentally alter model structure and numerical representations, but their impact can be difficult to interpret without visualization tools. Dedicated visualization frameworks and libraries help practitioners gain insights into how pruning, quantization, and other optimizations affect model behavior. These tools provide graphical representations of sparsity patterns, quantization error distributions, and activation changes, making optimization more transparent and controllable.

Visualizing Quantization

Quantization reduces numerical precision, introducing rounding errors that can impact model accuracy. Visualization tools provide direct insight into how these errors are distributed, helping diagnose and mitigate precision-related performance degradation.

One commonly used technique is quantization error histograms, which depict the distribution of errors across weights and activations. These histograms reveal whether quantization errors follow a Gaussian distribution or contain outliers, which could indicate problematic layers. TensorFlow’s Quantization Debugger and PyTorch’s FX Graph Mode Quantization tools allow users to analyze such histograms and compare error patterns between different quantization methods.

Activation visualizations also help detect overflow issues caused by reduced numerical precision. Tools such as ONNX Runtime’s quantization visualization utilities and NVIDIA’s TensorRT Inspector allow practitioners to color-map activations before and after quantization, making saturation and truncation issues visible. This enables calibration adjustments to prevent excessive information loss, preserving numerical stability. For example, Figure 10.23 is a color mapping of the AlexNet convolutional kernels.

Figure 10.23: Color mapping of activations. Source: Krizhevsky, Sutskever, and Hinton (2017).

Beyond static visualizations, tracking quantization error over the training process is essential. Monitoring mean squared quantization error (MSQE) during quantization-aware training (QAT) helps identify divergence points where numerical precision significantly impacts learning. TensorBoard and PyTorch’s quantization debugging APIs provide real-time tracking, highlighting instability during training.

By integrating these visualization tools into optimization workflows, practitioners can identify and correct issues early, ensuring optimized models maintain both accuracy and efficiency. These empirical insights provide a deeper understanding of how sparsity, quantization, and architectural optimizations affect models, guiding effective model compression and deployment strategies.

Visualizing Sparsity

Sparsity visualization tools provide detailed insight into pruned models by mapping out which weights have been removed and how sparsity is distributed across different layers. Frameworks such as TensorBoard (for TensorFlow) and Netron (for ONNX) allow users to inspect pruned networks at both the layer and weight levels.

One common visualization technique is sparsity heat maps, where color gradients indicate the proportion of weights removed from each layer. Layers with higher sparsity appear darker, revealing the model regions most impacted by pruning, as shown in Figure 10.24. This type of visualization transforms pruning from a black-box operation into an interpretable process, enabling practitioners to better understand and control sparsity-aware optimizations.

Figure 10.24: Sparse network heat map. Source: Numenta.

Beyond static snapshots, trend plots track sparsity progression across multiple pruning iterations. These visualizations illustrate how global model sparsity evolves, often showing an initial rapid increase followed by more gradual refinements. Tools like TensorFlow’s Model Optimization Toolkit and SparseML’s monitoring utilities provide such tracking capabilities, displaying per-layer pruning levels over time. These insights allow practitioners to fine-tune pruning strategies by adjusting sparsity constraints for individual layers.

Libraries such as DeepSparse’s visualization suite and PyTorch’s pruning utilities enable the generation of these visualization tools, helping analyze how pruning decisions affect different model components. By making sparsity data visually accessible, these tools help practitioners optimize their models more effectively.

10.9 Conclusion

This chapter has explored the multifaceted landscape of model optimization, a critical process for translating machine learning advancements into practical, real-world systems. We began by recognizing the inherent tension between model accuracy and efficiency, driven by constraints such as computational cost, memory limitations, and energy consumption. This necessitates a systematic approach to refining models, ensuring they remain effective while operating within the boundaries of real-world deployment environments.

We examined three core dimensions of model optimization: optimizing model representation, numerical precision, and architectural efficiency. Within each dimension, we delved into specific techniques, such as pruning, knowledge distillation, quantization, and dynamic computation, highlighting their trade-offs and practical considerations. We also emphasized the importance of hardware-aware model design, recognizing that aligning model architectures with the underlying hardware capabilities is crucial for maximizing performance and efficiency.

Finally, we explored AutoML as a holistic approach to model optimization, automating many of the tasks that traditionally require manual effort and expertise. AutoML frameworks offer a unified approach to architecture search, hyperparameter tuning, model compression, and data processing, streamlining the optimization process and potentially leading to novel solutions that might be overlooked through manual exploration.

As machine learning continues to evolve, model optimization will remain a critical area of focus. The ongoing development of new techniques, coupled with advancements in hardware and software infrastructure, will further enhance our ability to deploy efficient, scalable, and robust AI systems. By understanding the principles and practices of model optimization, practitioners can effectively bridge the gap between theoretical advancements and practical applications, unlocking the full potential of machine learning to address real-world challenges.