DL Primer
DALL·E 3 Prompt: A rectangular illustration divided into two halves on a clean white background. The left side features a detailed and colorful depiction of a biological neural network, showing interconnected neurons with glowing synapses and dendrites. The right side displays a sleek and modern artificial neural network, represented by a grid of interconnected nodes and edges resembling a digital circuit. The transition between the two sides is distinct but harmonious, with each half clearly illustrating its respective theme: biological on the left and artificial on the right.

Purpose
What inspiration from nature drives the development of machine learning systems, and how do biological neural processes inform their fundamental design?
The neural systems of nature offer profound insights into information processing and adaptation, inspiring the core principles of modern machine learning. Translating biological mechanisms into computational frameworks illuminates fundamental patterns that shape artificial neural networks. These patterns reveal essential relationships between biological principles and their digital counterparts, establishing building blocks for understanding more complex architectures. Analyzing these mappings from natural to artificial provides critical insights into system design, laying the foundation for exploring advanced neural architectures and their practical implementations.
Understand the biological inspiration for artificial neural networks and how this foundation informs their design and function.
Explore the fundamental structure of neural networks, including neurons, layers, and connections.
Examine the processes of forward propagation, backward propagation, and optimization as the core mechanisms of learning.
Understand the complete machine learning pipeline, from pre-processing through neural computation to post-processing.
Compare and contrast training and inference phases, understanding their distinct computational requirements and optimizations.
Learn how neural networks process data to extract patterns and make predictions, bridging theoretical concepts with computational implementations.
Overview
Neural networks, a foundational concept within machine learning and artificial intelligence, are computational models inspired by the structure and function of biological neural systems. These networks represent a critical intersection of algorithms, mathematical frameworks, and computing infrastructure, making them integral to solving complex problems in AI.
When studying neural networks, it is helpful to place them within the broader hierarchy of AI and machine learning. Figure 1 provides a visual representation of this context. AI, as the overarching field, encompasses all computational methods that aim to mimic human cognitive functions. Within AI, machine learning includes techniques that enable systems to learn patterns from data. Neural networks, a key subset of ML, form the backbone of more advanced learning systems, including deep learning, by modeling complex relationships in data through interconnected computational units.
The emergence of neural networks reflects key shifts in how AI systems process information across three fundamental dimensions:
Data: From manually structured and rule-based datasets to raw, high-dimensional data. Neural networks are particularly adept at learning from complex and unstructured data, making them essential for tasks involving images, speech, and text.
Algorithms: From explicitly programmed rules to adaptive systems capable of learning patterns directly from data. Neural networks eliminate the need for manual feature engineering by discovering representations automatically through layers of interconnected units.
Computation: From simple, sequential operations to massively parallel computations. The scalability of neural networks has driven demand for advanced hardware, such as GPUs, that can efficiently process large models and datasets.
These shifts emphasize the importance of understanding neural networks, not only as mathematical constructs but also as practical components of real-world AI systems. The development and deployment of neural networks require careful consideration of computational efficiency, data processing workflows, and hardware optimization. To build a strong foundation, this chapter focuses on the core principles of neural networks, exploring their structure, functionality, and learning mechanisms. By understanding these basics, readers will be well-prepared to delve into more advanced architectures and their systems-level implications in later chapters.
The Evolution to Deep Learning
The current era of AI represents a transformative advance in computational problem-solving, marking the latest stage in an evolution from rule-based programming through classical machine learning to modern neural networks. To understand its significance, we must trace this progression and examine how each approach builds upon and addresses the limitations of its predecessors.
Rule-Based Programming
Traditional programming requires developers to explicitly define rules that tell computers how to process inputs and produce outputs. Consider a simple game like Breakout, shown in Figure 2. The program needs explicit rules for every interaction: when the ball hits a brick, the code must specify that the brick should be removed and the ball’s direction should be reversed. While this approach works well for games with clear physics and limited states, it demonstrates an inherent limitation of rule-based systems.
This rules-based paradigm extends to all traditional programming, as illustrated in Figure 3. The program takes both rules for processing and input data to produce outputs. Early artificial intelligence research explored whether this approach could scale to solve complex problems by encoding sufficient rules to capture intelligent behavior.
However, the limitations of rule-based approaches become evident when addressing complex real-world tasks. Consider the problem of recognizing human activities, shown in Figure 4. Initial rules might appear straightforward: classify movement below 4 mph as walking and faster movement as running. Yet real-world complexity quickly emerges. The classification must account for variations in speed, transitions between activities, and numerous edge cases. Each new consideration requires additional rules, leading to increasingly complex decision trees.
This challenge extends to computer vision tasks. Detecting objects like cats in images would require rules about System Implications: pointed ears, whiskers, typical body shapes. Such rules would need to account for variations in viewing angle, lighting conditions, partial occlusions, and natural variations among instances. Early computer vision systems attempted this approach through geometric rules but achieved success only in controlled environments with well-defined objects.
This knowledge engineering approach1 characterized artificial intelligence research in the 1970s and 1980s. Expert systems2 encoded domain knowledge as explicit rules, showing promise in specific domains with well-defined parameters but struggling with tasks humans perform naturally, such as object recognition, speech understanding, or natural language interpretation. These limitations highlighted a fundamental challenge: many aspects of intelligent behavior rely on implicit knowledge that resists explicit rule-based representation.
1 Knowledge Engineering: The process of creating rules and heuristics for problem-solving and decision-making within artificial intelligence systems.
2 Expert systems: An AI program that leverages expert knowledge in a particular field to answer questions or solve problems.
Classical Machine Learning
The limitations of pure rule-based systems led researchers to explore approaches that could learn from data. Machine learning offered a promising direction: instead of writing rules for every situation, we could write programs that found patterns in examples. However, the success of these methods still depended heavily on human insight to define what patterns might be important, a process known as feature engineering3.
3 Feature engineering: The process of using domain knowledge to create features that make machine learning algorithms work.
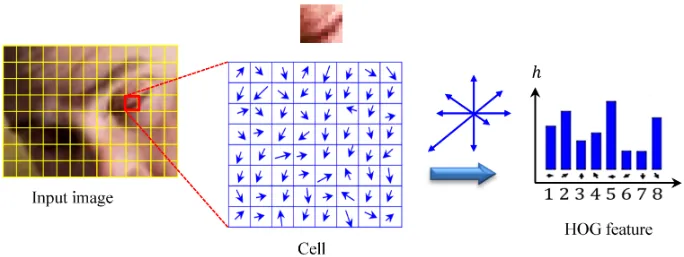
Feature engineering involves transforming raw data into representations that make patterns more apparent to learning algorithms. In computer vision, researchers developed sophisticated methods to extract meaningful patterns from images. The Histogram of Oriented Gradients (HOG) method, shown in Figure 5, exemplifies this approach. HOG works by first identifying edges in an image, which are places where brightness changes sharply and often indicate object boundaries. It then divides the image into small cells and measures how edges are oriented within each cell, summarizing these orientations in a histogram. This transformation converts raw pixel values into a representation that captures important shape information while being robust to variations in lighting and small changes in position.
Other feature extraction methods like SIFT (Scale-Invariant Feature Transform) and Gabor filters provided different ways to capture patterns in images. SIFT found distinctive points that could be recognized even when an object’s size or orientation changed. Gabor filters helped identify textures and repeated patterns. Each method encoded different types of human insight about what makes visual patterns recognizable.
These engineered features enabled significant advances in computer vision during the 2000s. Systems could now recognize objects with some robustness to real-world variations, leading to applications in face detection, pedestrian detection, and object recognition. However, the approach had fundamental limitations. Experts needed to carefully design feature extractors for each new problem, and the resulting features might miss important patterns that weren’t anticipated in their design.
Neural Networks and Representation Learning
Neural networks represent a fundamental shift in how we approach problem solving with computers, establishing a new programming paradigm that learns from data rather than following explicit rules. This shift becomes particularly evident when considering tasks like computer vision—specifically, identifying objects in images.
Deep Learning is a subfield of machine learning that utilizes artificial neural networks with multiple layers to automatically learn hierarchical representations from data. This approach enables the extraction of complex patterns from large datasets, facilitating tasks like image recognition, natural language processing, and speech recognition without explicit feature engineering. Deep learning’s effectiveness arises from its ability to learn features directly from raw data, adapt to diverse data structures, and scale with increasing data volume.
Unlike traditional programming approaches that require manual rule specification, deep learning utilizes artificial neural networks with multiple layers to automatically learn hierarchical representations from data. This enables systems to extract complex patterns from large datasets, facilitating tasks like image recognition, natural language processing, and speech recognition without explicit feature engineering. The effectiveness of deep learning comes from its ability to learn features directly from raw data, adapt to diverse data structures, and scale with increasing data volume.
Deep learning fundamentally differs by learning directly from raw data. Traditional programming, as we saw earlier in Figure 3, required both rules and data as inputs to produce answers. Machine learning inverts this relationship, as shown in Figure 6. Instead of writing rules, we provide examples (data) and their correct answers to discover the underlying rules automatically. This shift eliminates the need for humans to specify what patterns are important.
The system discovers these patterns automatically from examples. When shown millions of images of cats, the system learns to identify increasingly complex visual patterns, from simple edges to more sophisticated combinations that make up cat-like features. This mirrors how our own visual system works, building up understanding from basic visual elements to complex objects.
Unlike traditional approaches where performance often plateaus with more data and computation, deep learning systems continue to improve as we provide more resources. More training examples help the system recognize more variations and nuances. More computational power enables the system to discover more subtle patterns. This scalability has led to dramatic improvements in performance; for example, the accuracy of image recognition systems has improved from 74% in 2012 to over 95% today.
This different approach has profound implications for how we build AI systems. Deep learning’s ability to learn directly from raw data eliminates the need for manual feature engineering, but it comes with new demands. We need sophisticated infrastructure to handle massive datasets, powerful computers to process this data, and specialized hardware to perform the complex mathematical calculations efficiently. The computational requirements of deep learning have even driven the development of new types of computer chips optimized for these calculations.
The success of deep learning in computer vision exemplifies how this approach, when given sufficient data and computation, can surpass traditional methods. This pattern has repeated across many domains, from speech recognition to game playing, establishing deep learning as a transformative approach to artificial intelligence.
Neural System Implications
The progression from traditional programming to deep learning represents not just a shift in how we solve problems, but a fundamental transformation in computing system requirements. This transformation becomes particularly critical when we consider the full spectrum of ML systems, from massive cloud deployments to resource-constrained Tiny ML devices.
Traditional programs follow predictable patterns. They execute sequential instructions, access memory in regular patterns, and utilize computing resources in well-understood ways. A typical rule-based image processing system might scan through pixels methodically, applying fixed operations with modest and predictable computational and memory requirements. These characteristics made traditional programs relatively straightforward to deploy across different computing platforms.
Machine learning with engineered features introduced new complexities. Feature extraction algorithms required more intensive computation and structured data movement. The HOG feature extractor discussed earlier, for instance, requires multiple passes over image data, computing gradients and constructing histograms. While this increased both computational demands and memory complexity, the resource requirements remained relatively predictable and scalable across platforms.
Deep learning, however, fundamentally reshapes system requirements across multiple dimensions. Table 1 shows the evolution of system requirements across programming paradigms:
| System Aspect | Traditional Programming | ML with Features | Deep Learning |
|---|---|---|---|
| Computation | Sequential, predictable paths | Structured parallel operations | Massive matrix parallelism |
| Memory Access | Small, predictable patterns | Medium, batch-oriented | Large, complex hierarchical patterns |
| Data Movement | Simple input/output flows | Structured batch processing | Intensive cross-system movement |
| Hardware Needs | CPU-centric | CPU with vector units | Specialized accelerators |
| Resource Scaling | Fixed requirements | Linear with data size | Exponential with complexity |
These differences manifest in several critical ways, with implications across the entire ML systems spectrum.
Computation Patterns
While traditional programs follow sequential logic flows, deep learning requires massive parallel operations on matrices. This shift explains why conventional CPUs, designed for sequential processing, prove inefficient for neural network computations. The need for parallel processing has driven the adoption of specialized hardware architectures, ranging from powerful cloud GPUs to specialized mobile processors to Tiny ML accelerators.
Memory Systems
Traditional programs typically maintain small, fixed memory footprints. Deep learning models, however, must manage parameters across complex memory hierarchies. Memory bandwidth often becomes the primary performance bottleneck, creating particular challenges for resource-constrained systems. This drives different optimization strategies across the ML systems spectrum, ranging from memory-rich cloud deployments to heavily optimized Tiny ML implementations.
System Scaling
Perhaps most importantly, deep learning fundamentally changes how systems scale and the critical importance of efficiency. Traditional programs have relatively fixed resource requirements with predictable performance characteristics. Deep learning systems, however, can consume exponentially more resources as models grow in complexity. This relationship between model capability and resource consumption makes system efficiency a central concern.
The need to bridge algorithmic concepts with hardware realities becomes crucial. While traditional programs map relatively straightforwardly to standard computer architectures, deep learning requires us to think carefully about:
- How to efficiently map matrix operations to physical hardware
- Ways to minimize data movement across memory hierarchies
- Methods to balance computational capability with resource constraints
- Techniques to optimize both algorithm and system-level efficiency
These fundamental shifts explain why deep learning has spurred innovations across the entire computing stack. From specialized hardware accelerators4 to new memory architectures5 to sophisticated software frameworks, the demands of deep learning continue to reshape computer system design. Interestingly, many of these challenges, efficiency, scaling, and adaptability, are ones that biological systems have already solved. This brings us to a critical question: what can we learn from nature’s own information processing system and strive to mimic them as artificially intelligent systems.
4 Hardware accelerators: Specialized hardware designed to perform certain types of operations more efficiently than general-purpose computing units.
5 Memory architecture: The design of a computer’s memory system, including the physical structure and components, data organization and access, and pathways between memory and computing units.
Biological to Artificial Neurons
The quest to create artificial intelligence has been profoundly influenced by our understanding of biological intelligence, particularly the human brain. This isn’t surprising; the brain represents the most sophisticated information processing system we know of. It is capable of learning, adapting, and solving complex problems while maintaining remarkable energy efficiency. The way our brains function has provided fundamental insights that continue to shape how we approach artificial intelligence.
Biological Intelligence
When we observe biological intelligence, several key principles emerge. The brain demonstrates an extraordinary ability to learn from experience, constantly modifying its neural connections based on new information and interactions with the environment. This adaptability is fundamental; every experience potentially alters the brain’s structure and refines its responses for future situations. This biological capability directly inspired one of the core principles of machine learning: the ability to learn and improve from data rather than following fixed, pre-programmed rules.
Another striking feature of biological intelligence is its parallel processing capability. The brain processes vast amounts of information simultaneously, with different regions specializing in specific functions while working in concert. This distributed, parallel architecture stands in stark contrast to traditional sequential computing and has significantly influenced modern AI system design. The brain’s ability to efficiently coordinate these parallel processes while maintaining coherent function represents a level of sophistication we’re still working to fully understand and replicate.
The brain’s pattern recognition capabilities are particularly noteworthy. Biological systems excel at identifying patterns in complex, noisy data, whether it is recognizing faces in a crowd, understanding speech in a noisy environment, or identifying objects from partial information. This remarkable ability has inspired numerous AI applications, particularly in computer vision and speech recognition systems. The brain accomplishes these tasks with an efficiency that artificial systems are still striving to match.
Perhaps most remarkably, biological systems achieve all this with incredible energy efficiency. The human brain operates on approximately 20 watts of power, about the same as a low-power light bulb, while performing complex cognitive tasks that would require orders of magnitude more power in current artificial systems. This efficiency hasn’t just impressed researchers; it has become a crucial goal in the development of AI hardware and algorithms.
These biological principles have led to two distinct but complementary approaches in artificial intelligence. The first attempts to directly mimic neural structure and function, leading to artificial neural networks and deep learning architectures that structurally resemble biological neural networks. The second takes a more abstract approach, adapting biological principles to work efficiently within the constraints of computer hardware without necessarily copying biological structures exactly. In the following sections, we will explore how these approaches manifest in practice, beginning with the fundamental building block of neural networks: the neuron itself.
Transition to Artificial Neurons
To understand how biological principles translate into artificial systems, we must first examine the basic unit of biological information processing: the neuron. This cellular building block provides the blueprint for its artificial counterpart and helps us understand how complex neural networks emerge from simple components working in concert.
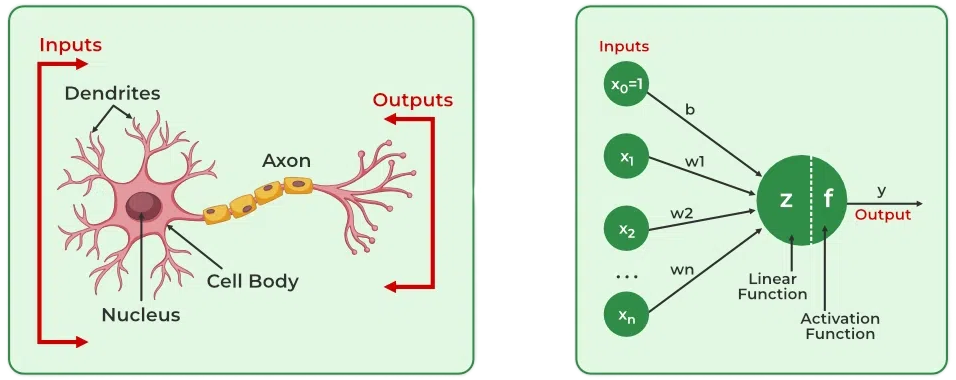
In biological systems, the neuron (or cell) is the basic functional unit of the nervous system. Understanding its structure is crucial before we draw parallels to artificial systems. Figure 7 illustrates the structure of a biological neuron.
A biological neuron consists of several key components. The central part is the cell body, or soma, which contains the nucleus and performs the cell’s basic life processes. Extending from the soma are branch-like structures called dendrites, which act as receivers for incoming signals from other neurons. The connections between neurons occur at synapses, which modulate the strength of the transmitted signals. Finally, a long, slender projection called the axon conducts electrical impulses away from the cell body to other neurons.
The neuron functions as follows: Dendrites act as receivers, collecting input signals from other neurons. Synapses at these connections modulate the strength of each signal, determining how much influence each input has. The soma integrates these weighted signals and decides whether to trigger an output signal. If triggered, the axon transmits this signal to other neurons.
Each element of a biological neuron has a computational analog in artificial systems, reflecting the principles of learning, adaptability, and efficiency found in nature. To better understand how biological intelligence informs artificial systems, Table 2 captures the mapping between the components of biological and artificial neurons. This should be viewed alongside Figure 7 for a complete picture. Together, they paint a picture of the biological-to-artificial neuron mapping.
| Biological Neuron | Artificial Neuron |
|---|---|
| Cell | Neuron / Node |
| Dendrites | Inputs |
| Synapses | Weights |
| Soma | Net Input |
| Axon | Output |
Each component serves a similar function, albeit through vastly different mechanisms. Here, we explain these mappings and their implications for artificial neural networks.
Cell \(\longleftrightarrow\) Neuron/Node: The artificial neuron or node serves as the fundamental computational unit, mirroring the cell’s role in biological systems.
Dendrites \(\longleftrightarrow\) Inputs: Dendrites in biological neurons receive incoming signals from other neurons, analogous to how inputs feed into artificial neurons. They act as the signal receivers, like antennas collecting information.
Synapses \(\longleftrightarrow\) Weights: Synapses modulate the strength of connections between neurons, directly analogous to weights in artificial neurons. These weights are adjustable, enabling learning and optimization over time by controlling how much influence each input has.
Soma \(\longleftrightarrow\) Net Input: The net input in artificial neurons sums weighted inputs to determine activation, similar to how the soma integrates signals in biological neurons.
Axon \(\longleftrightarrow\) Output: The output of an artificial neuron passes processed information to subsequent network layers, much like an axon transmits signals to other neurons.
This mapping illustrates how artificial neural networks simplify and abstract biological processes while preserving their essential computational principles. However, understanding individual neurons is just the beginning—the true power of neural networks emerges from how these basic units work together in larger systems.
Artificial Intelligence
The translation from biological principles to artificial computation requires a deep appreciation of what makes biological neural networks so effective at both the cellular and network levels. The brain processes information through distributed computation across billions of neurons, each operating relatively slowly compared to silicon transistors. A biological neuron fires at approximately 200 Hz, while modern processors operate at gigahertz frequencies. Despite this speed limitation, the brain’s parallel architecture enables sophisticated real-time processing of complex sensory input, decision making, and control of behavior.
This computational efficiency emerges from the brain’s basic organizational principles. Each neuron acts as a simple processing unit, integrating inputs from thousands of other neurons and producing a binary output signal based on whether this integrated input exceeds a threshold. The connection strengths between neurons, mediated by synapses, are continuously modified through experience. This synaptic plasticity6 forms the basis for learning and adaptation in biological neural networks. These biological principles suggest key computational elements needed in artificial neural systems:
6 Synaptic Plasticity: The ability of connections between neurons to change in strength in response to changes in synaptic activity.
- Simple processing units that integrate multiple inputs
- Adjustable connection strengths between units
- Nonlinear activation based on input thresholds
- Parallel processing architecture
- Learning through modification of connection strengths
Computational Translation
We face the challenge of capturing the essence of neural computation within the rigid framework of digital systems. The implementation of biological principles in artificial neural systems represents a nuanced balance between biological fidelity and computational efficiency. At its core, an artificial neuron captures the essential computational properties of its biological counterpart through mathematical operations that can be efficiently executed on digital hardware.
Table 3 provides a systematic view of how key biological features map to their computational counterparts. Each biological feature has an analog in computational systems, revealing both the possibilities and limitations of digital neural implementation, which we will learn more about later.
The basic computational unit in artificial neural networks, the artificial neuron, simplifies the complex electrochemical processes of biological neurons into three fundamental operations. First, input signals are weighted, mimicking how biological synapses modulate incoming signals with different strengths. Second, these weighted inputs are summed together, analogous to how a biological neuron integrates incoming signals in its cell body. Finally, the summed input passes through an activation function that determines the neuron’s output, similar to how a biological neuron fires based on whether its membrane potential exceeds a threshold.
| Biological Feature | Computational Translation |
|---|---|
| Neuron firing | Activation function |
| Synaptic strength | Weighted connections |
| Signal integration | Summation operation |
| Distributed memory | Weight matrices |
| Parallel processing | Concurrent computation |
This mathematical abstraction preserves key computational principles while enabling efficient digital implementation. The weighting of inputs allows the network to learn which connections are important, just as biological neural networks strengthen or weaken synaptic connections through experience. The summation operation captures how biological neurons integrate multiple inputs into a single decision. The activation function introduces nonlinearity essential for learning complex patterns, much like the threshold-based firing of biological neurons.
Memory in artificial neural networks takes a markedly different form from biological systems. While biological memories are distributed across synaptic connections and neural patterns, artificial networks store information in discrete weights and parameters. This architectural difference reflects the constraints of current computing hardware, where memory and processing are physically separated rather than integrated as in biological systems. Despite these implementation differences, artificial neural networks achieve similar functional capabilities in pattern recognition and learning.
The brain’s massive parallelism represents a fundamental challenge in artificial implementation. While biological neural networks process information through billions of neurons operating simultaneously, artificial systems approximate this parallelism through specialized hardware like GPUs and tensor processing units. These devices efficiently compute the matrix operations that form the mathematical foundation of artificial neural networks, achieving parallel processing at a different scale and granularity than biological systems.
System Requirements
The computational translation of neural principles creates specific demands on the underlying computing infrastructure. These requirements emerge from the fundamental differences between biological and artificial implementations of neural processing, shaping how we design and build systems capable of supporting artificial neural networks.
Table 4 shows how each computational element drives particular system requirements. From this mapping, we can see how the choices made in computational translation directly influence the hardware and system architecture needed for implementation.
| Computational Element | System Requirements |
|---|---|
| Activation functions | Fast nonlinear operation units |
| Weight operations | High-bandwidth memory access |
| Parallel computation | Specialized parallel processors |
| Weight storage | Large-scale memory systems |
| Learning algorithms | Gradient computation hardware |
Storage architecture represents a critical requirement, driven by the fundamental difference in how biological and artificial systems handle memory. In biological systems, memory and processing are intrinsically integrated—synapses both store connection strengths and process signals. Artificial systems, however, must maintain a clear separation between processing units and memory. This creates a need for both high-capacity storage to hold millions or billions of connection weights and high-bandwidth pathways to move this data quickly between storage and processing units. The efficiency of this data movement often becomes a critical bottleneck that biological systems do not face.
The learning process itself imposes distinct requirements on artificial systems. While biological networks modify synaptic strengths through local chemical processes, artificial networks must coordinate weight updates across the entire network. This creates substantial computational and memory demands during training—systems must not only store current weights but also maintain space for gradients and intermediate calculations. The requirement to backpropagate error signals7, with no real biological analog, further complicates the system architecture.
7 Backpropagation: A common method used to train artificial neural networks. It calculates the gradient of the loss function with respect to the weights of the network.
Energy efficiency emerges as a final critical requirement, highlighting perhaps the starkest contrast between biological and artificial implementations. The human brain’s remarkable energy efficiency, which operates on approximately 20 watts, stands in sharp contrast to the substantial power demands of artificial neural networks. Current systems often require orders of magnitude more energy to implement similar capabilities. This gap drives ongoing research in more efficient hardware architectures and has profound implications for the practical deployment of neural networks, particularly in resource-constrained environments like mobile devices or edge computing systems.
Evolution and Impact
We can now better appreciate how the field of deep learning evolved to meet these challenges through advances in hardware and algorithms. This journey began with early artificial neural networks in the 1950s, marked by the introduction of the Perceptron. While groundbreaking in concept, these early systems were severely limited by the computational capabilities of their era—primarily mainframe computers that lacked both the processing power and memory capacity needed for complex networks.
The development of backpropagation algorithms in the 1980s (Rumelhart, Hinton, and Williams 1986), which we will learn about later, represented a theoretical breakthrough and povided a systematic way to train multi-layer networks. However, the computational demands of this algorithm far exceeded available hardware capabilities. Training even modest networks could take weeks, making experimentation and practical applications challenging. This mismatch between algorithmic requirements and hardware capabilities contributed to a period of reduced interest in neural networks.
The term “deep learning” gained prominence in the 2010s, coinciding with significant advances in computational power and data accessibility. The field has since experienced exponential growth, as illustrated in Figure 8. The graph reveals two remarkable trends: computational capabilities measured in the number of Floating Point Operations per Second (FLOPS)8 initially followed a \(1.4\times\) improvement pattern from 1952 to 2010, then accelerated to a 3.4-month doubling cycle from 2012 to 2022. Perhaps more striking is the emergence of large-scale models between 2015 and 2022 (not explicitly shown or easily seen in the figure), which scaled 2 to 3 orders of magnitude faster than the general trend, following an aggressive 10-month doubling cycle.
8 Floating Point Operations per Second (FLOPS): A measure of computer performance, useful in fields of scientific computations that require floating-point calculations.
The evolutionary trends were driven by parallel advances across three fundamental dimensions: data availability, algorithmic innovations, and computing infrastructure. These three factors, namely, data, algorithms, and infrastructure, reinforced each other in a virtuous cycle that continues to drive progress in the field today. As Figure 9 shows, more powerful computing infrastructure enabled processing larger datasets. Larger datasets drove algorithmic innovations. Better algorithms demanded more sophisticated computing systems. This virtuous cycle continues to drive progress in the field today.
The data revolution transformed what was possible with neural networks. The rise of the internet and digital devices created unprecedented access to training data. Image sharing platforms provided millions of labeled images. Digital text collections enabled language processing at scale. Sensor networks and IoT devices generated continuous streams of real-world data. This abundance of data provided the raw material needed for neural networks to learn complex patterns effectively.
Algorithmic innovations made it possible to harness this data effectively. New methods for initializing networks and controlling learning rates made training more stable. Techniques for preventing overfitting allowed models to generalize better to new data. Most importantly, researchers discovered that neural network performance scaled predictably with model size, computation, and data quantity, leading to increasingly ambitious architectures.
Computing infrastructure evolved to meet these growing demands. On the hardware side, graphics processing units (GPUs) provided the parallel processing capabilities needed for efficient neural network computation. Specialized AI accelerators like TPUs (Jouppi et al. 2017) pushed performance further. High-bandwidth memory systems and fast interconnects addressed data movement challenges. Equally important were software advances—frameworks and libraries that made it easier to build and train networks, distributed computing systems that enabled training at scale, and tools for optimizing model deployment.
Neural Network Fundamentals
We can now examine the fundamental building blocks that make machine learning systems work. While the field has grown tremendously in sophistication, all modern neural networks, ranging from simple classifiers to large language models, share a common architectural foundation built upon basic computational units and principles.
This foundation begins with understanding how individual artificial neurons process information, how they are organized into layers, and how these layers are connected to form complete networks. By starting with these fundamental concepts, we can progressively build up to understanding more complex architectures and their applications.
Neural networks have come a long way since their inception in the 1950s, when the perceptron was first introduced. After a period of decline in popularity due to computational and theoretical limitations, the field saw a resurgence in the 2000s, driven by advancements in hardware (e.g., GPUs) and innovations like deep learning. These breakthroughs have made it possible to train networks with millions of parameters, enabling applications once considered impossible.
Basic Architecture
The architecture of a neural network determines how information flows through the system, from input to output. While modern networks can be tremendously complex, they all build upon a few key organizational principles that we will explore in the following sections. Understanding these principles is essential for both implementing neural networks and appreciating how they achieve their remarkable capabilities.
Neurons and Activations
The Perceptron is the basic unit or node that forms the foundation for more complex structures. It functions by taking multiple inputs, each representing a feature of the object under analysis, such as the characteristics of a home for predicting its price or the attributes of a song to forecast its popularity in music streaming services. These inputs are denoted as \(x_1, x_2, ..., x_n\). A perceptron can be configured to perform either regression or classification tasks. For regression, the actual numerical output \(\hat{y}\) is used. For classification, the output depends on whether \(\hat{y}\) crosses a certain threshold. If \(\hat{y}\) exceeds this threshold, the perceptron might output one class (e.g., ‘yes’), and if it does not, another class (e.g., ‘no’).
Figure 10 illustrates the fundamental building blocks of a perceptron, which serves as the foundation for more complex neural networks. A perceptron can be thought of as a miniature decision-maker, utilizing its weights, bias, and activation function to process inputs and generate outputs based on learned parameters. This concept forms the basis for understanding more intricate neural network architectures, such as multilayer perceptrons.
In these advanced structures, layers of perceptrons work in concert, with each layer’s output serving as the input for the subsequent layer. This hierarchical arrangement creates a deep learning model capable of comprehending and modeling complex, abstract patterns within data. By stacking these simple units, neural networks gain the ability to tackle increasingly sophisticated tasks, from image recognition to natural language processing.
Each input \(x_i\) has a corresponding weight \(w_{ij}\), and the perceptron simply multiplies each input by its matching weight. This operation is similar to linear regression, where the intermediate output, \(z\), is computed as the sum of the products of inputs and their weights: \[ z = \sum (x_i \cdot w_{ij}) \]
To this intermediate calculation, a bias term \(b\) is added, allowing the model to better fit the data by shifting the linear output function up or down. Thus, the intermediate linear combination computed by the perceptron including the bias becomes: \[ z = \sum (x_i \cdot w_{ij}) + b \]
Common activation functions include:9
9 Activation Function: A mathematical ‘gate’ in between the input from the previous layer and the output of the current layer, adding non-linearity to model complex patterns.
ReLU (Rectified Linear Unit): Defined as \(f(x) = \max(0,x)\), it introduces sparsity and accelerates convergence in deep networks. Its simplicity and effectiveness have made it the default choice in many modern architectures.
Sigmoid: Historically popular, the sigmoid function maps inputs to a range between 0 and 1 but is prone to vanishing gradients in deeper architectures. It’s particularly useful in binary classification problems where probabilities are needed.
Tanh: Similar to sigmoid but maps inputs to a range of \(-1\) to 1, centering the data. This centered output often leads to faster convergence in practice compared to sigmoid.
These activation functions transform the linear input sum into a non-linear output: \[ \hat{y} = \sigma(z) \]
Thus, the final output of the perceptron, including the activation function, can be expressed as:
Figure 11 shows an example where data exhibit a nonlinear pattern that could not be adequately modeled with a linear approach. The activation function enables the network to learn and represent complex relationships in the data, making it possible to solve sophisticated tasks like image recognition or speech processing.
Thus, the final output of the perceptron, including the activation function, can be expressed as: \[ z = \sigma\left(\sum (x_i \cdot w_{ij}) + b\right) \]
Layers and Connections
While a single perceptron can model simple decisions, the power of neural networks comes from combining multiple neurons into layers. A layer is a collection of neurons that process information in parallel. Each neuron in a layer operates independently on the same input but with its own set of weights and bias, allowing the layer to learn different features or patterns from the same input data.
In a typical neural network, we organize these layers hierarchically:
- Input Layer: Receives the raw data features
- Hidden Layers: Process and transform the data through multiple stages
- Output Layer: Produces the final prediction or decision
Figure 12 illustrates this layered architecture. When data flows through these layers, each successive layer transforms the representation of the data, gradually building more complex and abstract features. This hierarchical processing is what gives deep neural networks their remarkable ability to learn complex patterns.
Neural Network - 3Blue1Brown
Data Flow and Transformations
As data flows through the network, it is transformed at each layer (l) to extract meaningful patterns. Each layer combines the input data using learned weights and biases, then applies an activation function to introduce non-linearity. This process can be written mathematically as: \[ \mathbf{z}^{(l)} = \mathbf{W}^{(l)}\mathbf{x}^{(l-1)} + \mathbf{b}^{(l)} \] Where:
\(\mathbf{x}^{(l-1)}\) is the input vector from the previous layer
\(\mathbf{W}^{(l)}\) is the weight matrix for the current layer
\(\mathbf{b}^{(l)}\) is the bias vector
\(\mathbf{z}^{(l)}\) is the pre-activation output10
10 Pre-activation output: The output produced by a neuron in a neural network before the activation function is applied.
Now that we have covered the basics, let’s look at how these concepts come together in practice. Neural networks excel at tasks like handwritten digit recognition, where they learn to identify patterns in pixel data and classify images into different categories. This practical example introduces some new concepts that we will explore in more depth soon.
Weights and Biases
Weight Matrices
Weights in neural networks determine how strongly inputs influence the output of a neuron. While we first discussed weights for a single perceptron, in larger networks, weights are organized into matrices for efficient computation across entire layers. For example, in a layer with \(n\) input features and \(m\) neurons, the weights form a matrix \(\mathbf{W} \in \mathbb{R}^{n \times m}\). Each column in this matrix represents the weights for a single neuron in the layer. This organization allows the network to process multiple inputs simultaneously, an essential feature for handling real-world data efficiently.
Let’s consider how this extends our previous perceptron equations to handle multiple neurons simultaneously. For a layer of \(m\) neurons, instead of computing each neuron’s output separately: \[ z_j = \sum_{i=1}^n (x_i \cdot w_{ij}) + b_j \]
We can compute all outputs at once using matrix multiplication: \[ \mathbf{z} = \mathbf{x}^T\mathbf{W} + \mathbf{b} \]
This matrix organization is more than just mathematical convenience; it reflects how modern neural networks are implemented for efficiency. Each weight \(w_{ij}\) represents the strength of the connection between input feature \(i\) and neuron \(j\) in the layer.
Connection Patterns
In the simplest and most common case, each neuron in a layer is connected to every neuron in the previous layer, forming what we call a “dense” or “fully-connected” layer. This pattern means that each neuron has the opportunity to learn from all available features from the previous layer.
Figure 13 illustrates these dense connections between layers. For a network with layers of sizes \((n_1, n_2, n_3)\), the weight matrices would have dimensions:
- Between first and second layer: \(\mathbf{W}^{(1)} \in \mathbb{R}^{n_1 \times n_2}\)
- Between second and third layer: \(\mathbf{W}^{(2)} \in \mathbb{R}^{n_2 \times n_3}\)
Bias Terms
Each neuron in a layer also has an associated bias term. While weights determine the relative importance of inputs, biases allow neurons to shift their activation functions. This shifting is crucial for learning, as it gives the network flexibility to fit more complex patterns.
For a layer with \(m\) neurons, the bias terms form a vector \(\mathbf{b} \in \mathbb{R}^m\). When we compute the layer’s output, this bias vector is added to the weighted sum of inputs: \[ \mathbf{z} = \mathbf{x}^T\mathbf{W} + \mathbf{b} \]
The bias terms effectively allow each neuron to have a different “threshold” for activation, making the network more expressive.
Parameter Organization
The organization of weights and biases across a neural network follows a systematic pattern. For a network with \(L\) layers, we maintain:
A weight matrix \(\mathbf{W}^{(l)}\) for each layer \(l\)
A bias vector \(\mathbf{b}^{(l)}\) for each layer \(l\)
Activation functions \(f^{(l)}\) for each layer \(l\)
This gives us the complete layer computation: \[ \mathbf{h}^{(l)} = f^{(l)}(\mathbf{z}^{(l)}) = f^{(l)}(\mathbf{h}^{(l-1)T}\mathbf{W}^{(l)} + \mathbf{b}^{(l)}) \] Where \(\mathbf{h}^{(l)}\) represents the layer’s output after applying the activation function.
Network Topology
Network topology describes how the basic building blocks we’ve discussed, such as neurons, layers, and connections, come together to form a complete neural network. We can best understand network topology through a concrete example. Consider the task of recognizing handwritten digits, a classic problem in deep learning using the MNIST11 dataset.
11 MNIST (Modified National Institute of Standards and Technology) is a large database of handwritten digits that has been widely used to train and test machine learning systems since its creation in 1998. The dataset consists of 60,000 training images and 10,000 testing images, each being a \(28\times 28\) pixel grayscale image of a single handwritten digit from 0 to 9.
Basic Structure
The fundamental structure of a neural network consists of three main components: input layer, hidden layers, and output layer. As shown in Figure 14\(\text{a)}\), a \(28\times 28\) pixel grayscale image of a handwritten digit must be processed through these layers to produce a classification output.
The input layer’s width is directly determined by our data format. As shown in Figure 14\(\text{b)}\), for a \(28\times 28\) pixel image, each pixel becomes an input feature, requiring 784 input neurons \((28\times 28 = 784)\). We can think of this either as a 2D grid of pixels or as a flattened vector of 784 values, where each value represents the intensity of one pixel.
The output layer’s structure is determined by our task requirements. For digit classification, we use 10 output neurons, one for each possible digit (0-9). When presented with an image, the network produces a value for each output neuron, where higher values indicate greater confidence that the image represents that particular digit.
Between these fixed input and output layers, we have flexibility in designing the hidden layer topology. The choice of hidden layer structure, including the number of layers to use and their respective widths, represents one of the fundamental design decisions in neural networks. Additional layers increase the network’s depth, allowing it to learn more abstract features through successive transformations. The width of each layer provides capacity for learning different features at each level of abstraction.
These basic topological choices have significant implications for both the network’s capabilities and its computational requirements. Each additional layer or neuron increases the number of parameters that must be stored and computed during both training and inference. However, without sufficient depth or width, the network may lack the capacity to learn complex patterns in the data.
Design Trade-offs
The design of neural network topology centers on three fundamental decisions: the number of layers (depth), the size of each layer (width), and how these layers connect. Each choice affects both the network’s learning capability and its computational requirements.
Network depth determines the level of abstraction the network can achieve. Each layer transforms its input into a new representation, and stacking multiple layers allows the network to build increasingly complex features. In our MNIST example, a deeper network might first learn to detect edges, then combine these edges into strokes, and finally assemble strokes into complete digit patterns. However, adding layers isn’t always beneficial—deeper networks increase computational cost substantially, can be harder to train due to vanishing gradients12, and may require more sophisticated training techniques.
12 Vanishing Gradients: Problem in deep learning where gradient becomes so small that the model stops (or significantly slows down) learning.
The width of each layer, which is determined by the number of neurons it contains, controls how much information the network can process in parallel at each stage. Wider layers can learn more features simultaneously but require proportionally more parameters and computation. For instance, if a hidden layer is processing edge features in our digit recognition task, its width determines how many different edge patterns it can detect simultaneously.
A very important consideration in topology design is the total parameter count. For a network with layers of size \((n_1, n_2, \ldots, n_L)\), each pair of adjacent layers \(l\) and \(l+1\) requires \(n_l \times n_{l+1}\) weight parameters, plus \(n_{l+1}\) bias parameters. These parameters must be stored in memory and updated during training, making the parameter count a key constraint in practical applications.
When designing networks, we need to balance learning capacity, computational efficiency, and ease of training. While the basic approach connects every neuron to every neuron in the next layer (fully connected), this isn’t always the most effective strategy. Sometimes, using fewer but more strategic connections, as seen in convolutional networks13, can achieve better results with less computation. Consider our MNIST example—when humans recognize digits, we don’t analyze every pixel independently but look for meaningful patterns like lines and curves. Similarly, we can design our network to focus on local patterns in the image rather than treating each pixel as completely independent.
13 Convolutional Networks (CNNs): A type of neural network architecture designed to process grid-structured input data, like images.
14 Residual Connections (Skip Connections): Shortcut connections between layers in a neural network, helping mitigate the vanishing gradient problem by allowing gradients to flow directly through the network.
Another important consideration is how information flows through the network. While the basic flow is from input to output, some network designs include additional paths for information to flow, such as skip connections or residual connections14. These alternative paths can make the network easier to train and more effective at learning complex patterns. Think of these as shortcuts that help information flow more directly when needed, similar to how our brain can combine both detailed and general impressions when recognizing objects.
These design decisions have significant practical implications for memory usage for storing network parameters, computational costs during both training and inference, training behavior and convergence, and the network’s ability to generalize to new examples. The optimal balance of these trade-offs depends heavily on your specific problem, available computational resources, and dataset characteristics. Successful network design requires carefully weighing these factors against practical constraints.
Connection Patterns
Neural networks can be structured with different connection patterns between layers, each offering distinct advantages for learning and computation. Understanding these fundamental patterns provides insight into how networks process information and learn representations from data.
Dense connectivity represents the standard pattern where each neuron connects to every neuron in the subsequent layer. In our MNIST example, connecting our 784-dimensional input layer to a hidden layer of 100 neurons requires 78,400 weight parameters. This full connectivity enables the network to learn arbitrary relationships between inputs and outputs, but the number of parameters scales quadratically with layer width.
Sparse connectivity patterns introduce purposeful restrictions in how neurons connect between layers. Rather than maintaining all possible connections, neurons connect to only a subset of neurons in the adjacent layer. This approach draws inspiration from biological neural systems, where neurons typically form connections with a limited number of other neurons. In visual processing tasks like our MNIST example, neurons might connect only to inputs representing nearby pixels, reflecting the local nature of visual features.
As networks grow deeper, the path from input to output becomes longer, potentially complicating the learning process. Skip connections address this by adding direct paths between non-adjacent layers. These connections provide alternative routes for information flow, supplementing the standard layer-by-layer progression. In our digit recognition example, skip connections might allow later layers to reference both high-level patterns and the original pixel values directly.
These connection patterns have significant implications for both the theoretical capabilities and practical implementation of neural networks. Dense connections maximize learning flexibility at the cost of computational efficiency. Sparse connections can reduce computational requirements while potentially improving the network’s ability to learn structured patterns. Skip connections help maintain effective information flow in deeper networks.
Parameter Considerations
The arrangement of parameters (weights and biases) in a neural network determines both its learning capacity and computational requirements. While topology defines the network’s structure, the initialization and organization of parameters plays a crucial role in learning and performance.
Parameter count grows with network width and depth. For our MNIST example, consider a network with a 784-dimensional input layer, two hidden layers of 100 neurons each, and a 10-neuron output layer. The first layer requires 78,400 weights and 100 biases, the second layer 10,000 weights and 100 biases, and the output layer 1,000 weights and 10 biases, totaling 89,610 parameters. Each must be stored in memory and updated during learning.
Parameter initialization is fundamental to network behavior. Setting all parameters to zero would cause neurons in a layer to behave identically, preventing diverse feature learning. Instead, weights are typically initialized randomly, while biases often start at small constant values or even zeros. The scale of these initial values matters significantly, as values that are too large or too small can lead to poor learning dynamics.
The distribution of parameters affects information flow through layers. In digit recognition, if weights are too small, important input details might not propagate to later layers. If too large, the network might amplify noise. Biases help adjust the activation threshold of each neuron, enabling the network to learn optimal decision boundaries.
Different architectures may impose specific constraints on parameter organization. Some share weights across network regions to encode position-invariant pattern recognition. Others might restrict certain weights to zero, implementing sparse connectivity patterns15.
15 Sparsity: In data structures, sparsity refers to elements being zero or absent. In neural networks, it can refer to the absence of connections between nodes.
Learning Process
Neural networks learn to perform tasks through a process of training on examples. This process transforms the network from its initial state, where its weights are randomly initialized, to a trained state where the weights encode meaningful patterns from the training data. Understanding this process is fundamental to both the theoretical foundations and practical implementations of deep learning systems.
Training Overview
The core principle of neural network training is supervised learning from labeled examples. Consider our MNIST digit recognition task: we have a dataset of 60,000 training images, each a \(28\times 28\) pixel grayscale image paired with its correct digit label. The network must learn the relationship between these images and their corresponding digits through an iterative process of prediction and weight adjustment.
Training operates as a loop, where each iteration involves processing a subset of training examples called a batch. For each batch, the network performs several key operations:
- Forward computation through the network layers to generate predictions
- Evaluation of prediction accuracy using a loss function16
- Computation of weight adjustments based on prediction errors
- Update of network weights to improve future predictions
16 Loss function: A method for evaluating how well the algorithm models the given training data. The lower the value, the better the model.
This process can be expressed mathematically. Given an input image \(x\) and its true label \(y\), the network computes its prediction: \[ \hat{y} = f(x; \theta) \] where \(f\) represents the neural network function and \(\theta\) represents all trainable parameters (weights and biases, which we discussed earlier). The network’s error is measured by a loss function \(L\): \[ \text{loss} = L(\hat{y}, y) \]
This error measurement drives the adjustment of network parameters through a process called “backpropagation,” which we will examine in detail later.
In practice, training operates on batches of examples rather than individual inputs. For the MNIST dataset, each training iteration might process, for example, 32, 64, or 128 images simultaneously. This batch processing serves two purposes: it enables efficient use of modern computing hardware through parallel processing, and it provides more stable parameter updates by averaging errors across multiple examples.
The training cycle continues until the network achieves sufficient accuracy or reaches a predetermined number of iterations. Throughout this process, the loss function serves as a guide, with its minimization indicating improved network performance.
Forward Propagation
Forward propagation, as illustrated in Figure 15, is the core computational process in a neural network, where input data flows through the network’s layers to generate predictions. Understanding this process is essential as it forms the foundation for both network inference and training. Let’s examine how forward propagation works using our MNIST digit recognition example.
When an image of a handwritten digit enters our network, it undergoes a series of transformations through the layers. Each transformation combines the weighted inputs with learned patterns to progressively extract relevant features. In our MNIST example, a \(28\times 28\) pixel image is processed through multiple layers to ultimately produce probabilities for each possible digit (0-9).
The process begins with the input layer, where each pixel’s grayscale value becomes an input feature. For MNIST, this means 784 input values \((28\times 28 = 784)\), each normalized between 0 and 1. These values then propagate forward through the hidden layers, where each neuron combines its inputs according to its learned weights and applies a nonlinear activation function.
Layer Computation
The forward computation through a neural network proceeds systematically, with each layer transforming its inputs into increasingly abstract representations. In our MNIST network, this transformation process occurs in distinct stages.
At each layer, the computation involves two key steps: a linear transformation of inputs followed by a nonlinear activation. The linear transformation combines all inputs to a neuron using learned weights and a bias term. For a single neuron receiving inputs from the previous layer, this computation takes the form: \[ z = \sum_{i=1}^n w_ix_i + b \] where \(w_i\) represents the weights, \(x_i\) the inputs, and \(b\) the bias term. For an entire layer of neurons, we can express this more efficiently using matrix operations: \[ \mathbf{Z}^{(l)} = \mathbf{W}^{(l)}\mathbf{A}^{(l-1)} + \mathbf{b}^{(l)} \]
Here, \(\mathbf{W}^{(l)}\) represents the weight matrix for layer \(l\), \(\mathbf{A}^{(l-1)}\) contains the activations from the previous layer, and \(\mathbf{b}^{(l)}\) is the bias vector.
Following this linear transformation, each layer applies a nonlinear activation function \(f\): \[ \mathbf{A}^{(l)} = f(\mathbf{Z}^{(l)}) \]
This process repeats at each layer, creating a chain of transformations:
Input → Linear Transform → Activation → Linear Transform → Activation → … → Output
In our MNIST example, the pixel values first undergo a transformation by the first hidden layer’s weights, converting the 784-dimensional input into an intermediate representation. Each subsequent layer further transforms this representation, ultimately producing a 10-dimensional output vector representing the network’s confidence in each possible digit.
Mathematical Representation
The complete forward propagation process can be expressed as a composition of functions, each representing a layer’s transformation. Let us formalize this mathematically, building on our MNIST example.
For a network with \(L\) layers, we can express the full forward computation as: \[ \mathbf{A}^{(L)} = f^{(L)}\Big(\mathbf{W}^{(L)}f^{(L-1)}\Big(\mathbf{W}^{(L-1)}\cdots\big(f^{(1)}(\mathbf{W}^{(1)}\mathbf{X} + \mathbf{b}^{(1)})\big)\cdots + \mathbf{b}^{(L-1)}\Big) + \mathbf{b}^{(L)}\Big) \]
While this nested expression captures the complete process, we typically compute it step by step:
First layer: \[ \mathbf{Z}^{(1)} = \mathbf{W}^{(1)}\mathbf{X} + \mathbf{b}^{(1)} \] \[ \mathbf{A}^{(1)} = f^{(1)}(\mathbf{Z}^{(1)}) \]
Hidden layers \((l = 2,\ldots, L-1)\): \[ \mathbf{Z}^{(l)} = \mathbf{W}^{(l)}\mathbf{A}^{(l-1)} + \mathbf{b}^{(l)} \] \[ \mathbf{A}^{(l)} = f^{(l)}(\mathbf{Z}^{(l)}) \]
Output layer: \[ \mathbf{Z}^{(L)} = \mathbf{W}^{(L)}\mathbf{A}^{(L-1)} + \mathbf{b}^{(L)} \] \[ \mathbf{A}^{(L)} = f^{(L)}(\mathbf{Z}^{(L)}) \]
In our MNIST example, if we have a batch of \(B\) images, the dimensions of these operations are:
- Input \(\mathbf{X}\): \(B \times 784\)
- First layer weights \(\mathbf{W}^{(1)}\): \(n_1\times 784\)
- Hidden layer weights \(\mathbf{W}^{(l)}\): \(n_l\times n_{l-1}\)
- Output layer weights \(\mathbf{W}^{(L)}\): \(n_{L-1}\times 10\)
Computational Process
To understand how these mathematical operations translate into actual computation, let’s walk through the forward propagation process for a batch of MNIST images. This process illustrates how data is transformed from raw pixel values to digit predictions.
Consider a batch of 32 images entering our network. Each image starts as a \(28\times 28\) grid of pixel values, which we flatten into a 784-dimensional vector. For the entire batch, this gives us an input matrix \(\mathbf{X}\) of size \(32\times 784\), where each row represents one image. The values are typically normalized to lie between 0 and 1.
The transformation at each layer proceeds as follows:
Input Layer Processing: The network takes our input matrix \(\mathbf{X}\) \((32\times 784)\) and transforms it using the first layer’s weights. If our first hidden layer has 128 neurons, \(\mathbf{W}^{(1)}\) is a \(784\times 128\) matrix. The resulting computation \(\mathbf{X}\mathbf{W}^{(1)}\) produces a \(32\times 128\) matrix.
Hidden Layer Transformations: Each element in this matrix then has its corresponding bias added and passes through an activation function. For example, with a ReLU activation, any negative values become zero while positive values remain unchanged. This nonlinear transformation enables the network to learn complex patterns in the data.
Output Generation: The final layer transforms its inputs into a \(32\times 10\) matrix, where each row contains 10 values corresponding to the network’s confidence scores for each possible digit. Often, these scores are converted to probabilities using a softmax function: \[ P(\text{digit } j) = \frac{e^{z_j}}{\sum_{k=1}^{10} e^{z_k}} \]
For each image in our batch, this gives us a probability distribution over the possible digits. The digit with the highest probability becomes the network’s prediction.
Practical Considerations
The implementation of forward propagation requires careful attention to several practical aspects that affect both computational efficiency and memory usage. These considerations become particularly important when processing large batches of data or working with deep networks.
Memory management plays an important role during forward propagation. Each layer’s activations must be stored for potential use in the backward pass during training. For our MNIST example with a batch size of 32, if we have three hidden layers of sizes 128, 256, and 128, the activation storage requirements are:
- First hidden layer: \(32\times 128 = 4,096\) values
- Second hidden layer: \(32\times 256 = 8,192\) values
- Third hidden layer: \(32\times 128 = 4,096\) values
- Output layer: \(32\times 10 = 320\) values
This gives us a total of 16,704 values that must be maintained in memory for each batch during training. The memory requirements scale linearly with batch size and can become substantial for larger networks.
Batch processing introduces important trade-offs. Larger batches enable more efficient matrix operations and better hardware utilization but require more memory. For example, doubling the batch size to 64 would double our memory requirements for activations. This relationship between batch size, memory usage, and computational efficiency often guides the choice of batch size in practice.
The organization of computations also affects performance. Matrix operations can be optimized through careful memory layout and the use of specialized libraries. The choice of activation functions impacts not only the network’s learning capabilities but also its computational efficiency, as some functions (like ReLU) are less expensive to compute than others (like tanh or sigmoid).
These considerations form the foundation for understanding the system requirements of neural networks, which we will explore in more detail in later chapters.
Loss Functions
Neural networks learn by measuring and minimizing their prediction errors. Loss functions provide the Algorithmic Structure for quantifying these errors, serving as the essential feedback mechanism that guides the learning process. Through loss functions, we can convert the abstract goal of “making good predictions” into a concrete optimization problem.
To understand the role of loss functions, let’s continue with our MNIST digit recognition example. When the network processes a handwritten digit image, it outputs ten numbers representing its confidence in each possible digit (0-9). The loss function measures how far these predictions deviate from the true answer. For instance, if an image shows a “7”, we want high confidence for digit “7” and low confidence for all other digits. The loss function penalizes the network when its prediction differs from this ideal.
Consider a concrete example: if the network sees an image of “7” and outputs confidences:
[0.1, 0.1, 0.1, 0.0, 0.0, 0.0, 0.2, 0.3, 0.1, 0.1]The highest confidence (0.3) is assigned to digit “7”, but this confidence is quite low, indicating uncertainty in the prediction. A good loss function would produce a high loss value here, signaling that the network needs significant improvement. Conversely, if the network outputs:
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.9, 0.0, 0.1]The loss function should produce a lower value, as this prediction is much closer to ideal.
Basic Concepts
A loss function measures how far the network’s predictions are from the correct answers. This difference is expressed as a single number: a lower loss means the predictions are more accurate, while a higher loss indicates the network needs improvement. During training, the loss function guides the network by helping it adjust its weights to make better predictions. For example, in recognizing handwritten digits, the loss will penalize predictions that assign low confidence to the correct digit.
Mathematically, a loss function \(L\) takes two inputs: the network’s predictions \(\hat{y}\) and the true values \(y\). For a single training example in our MNIST task: \[ L(\hat{y}, y) = \text{measure of discrepancy between prediction and truth} \]
When training with batches of data, we typically compute the average loss across all examples in the batch: \[ L_{\text{batch}} = \frac{1}{B}\sum_{i=1}^B L(\hat{y}_i, y_i) \] where \(B\) is the batch size and \((\hat{y}_i, y_i)\) represents the prediction and truth for the \(i\)-th example.
The choice of loss function depends on the type of task. For our MNIST classification problem, we need a loss function that can:
- Handle probability distributions over multiple classes
- Provide meaningful gradients for learning
- Penalize wrong predictions effectively
- Scale well with batch processing
Classification Losses
For classification tasks like MNIST digit recognition, “cross-entropy” loss17 has emerged as the standard choice. This loss function is particularly well-suited for comparing predicted probability distributions with true class labels.
17 Cross-Entropy Loss: A type of loss function that measures the difference between two probability distributions.
For a single digit image, our network outputs a probability distribution over the ten possible digits. We represent the true label as a one-hot vector where all entries are 0 except for a 1 at the correct digit’s position. For instance, if the true digit is “7”, the label would be: \[ y = \big[0, 0, 0, 0, 0, 0, 0, 1, 0, 0\big] \]
The cross-entropy loss for this example is: \[ L(\hat{y}, y) = -\sum_{j=1}^{10} y_j \log(\hat{y}_j) \] where \(\hat{y}_j\) represents the network’s predicted probability for digit j. Given our one-hot encoding, this simplifies to: \[ L(\hat{y}, y) = -\log(\hat{y}_c) \] where \(c\) is the index of the correct class. This means the loss depends only on the predicted probability for the correct digit—the network is penalized based on how confident it is in the right answer.
For example, if our network predicts the following probabilities for an image of “7”:
Predicted: [0.1, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.8, 0.0, 0.1]
True: [0, 0, 0, 0, 0, 0, 0, 1, 0, 0]The loss would be \(-\log(0.8)\), which is approximately 0.223. If the network were more confident and predicted 0.9 for the correct digit, the loss would decrease to approximately 0.105.
Loss Computation
The practical computation of loss involves considerations for both numerical stability and batch processing. When working with batches of data, we compute the average loss across all examples in the batch.
For a batch of B examples, the cross-entropy loss becomes: \[ L_{\text{batch}} = -\frac{1}{B}\sum_{i=1}^B \sum_{j=1}^{10} y_{ij} \log(\hat{y}_{ij}) \]
Computing this loss efficiently requires careful consideration of numerical precision. Taking the logarithm of very small probabilities can lead to numerical instability. Consider a case where our network predicts a probability of 0.0001 for the correct class. Computing \(\log(0.0001)\) directly might cause underflow or result in imprecise values.
To address this, we typically implement the loss computation with two key modifications:
Add a small epsilon to prevent taking log of zero: \[ L = -\log(\hat{y} + \epsilon) \]
Apply the log-sum-exp trick18 for numerical stability: \[ \text{softmax}(z_i) = \frac{\exp\big(z_i - \max(z)\big)}{\sum_j \exp\big(z_j - \max(z)\big)} \]
18 Log-Sum-Exp trick: A method used in machine learning to prevent numerical underflow and overflow by normalizing the inputs of exponentiated operations.
For our MNIST example with a batch size of 32, this means:
- Processing 32 sets of 10 probabilities
- Computing 32 individual loss values
- Averaging these values to produce the final batch loss
Training Implications
Understanding how loss functions influence training helps explain key implementation decisions in deep learning systems.
During each training iteration, the loss value serves multiple purposes:
- Performance Metric: It quantifies current network accuracy
- Optimization Target: Its gradients guide weight updates
- Convergence Signal: Its trend indicates training progress
For our MNIST classifier, monitoring the loss during training reveals the network’s learning trajectory. A typical pattern might show:
- Initial high loss (\(\sim 2.3\), equivalent to random guessing among 10 classes)
- Rapid decrease in early training iterations
- Gradual improvement as the network fine-tunes its predictions
- Eventually stabilizing at a lower loss (\(\sim 0.1\), indicating confident correct predictions)
The loss function’s gradients with respect to the network’s outputs provide the initial error signal that drives backpropagation. For cross-entropy loss, these gradients have a particularly simple form: the difference between predicted and true probabilities. This mathematical property makes cross-entropy loss especially suitable for classification tasks, as it provides strong gradients even when predictions are very wrong.
The choice of loss function also influences other training decisions:
- Learning rate selection (larger loss gradients might require smaller learning rates)
- Batch size (loss averaging across batches affects gradient stability)
- Optimization algorithm behavior
- Convergence criteria
Backward Propagation
Backward propagation, often called backpropagation, is the algorithmic cornerstone of neural network training. While forward propagation computes predictions, backward propagation determines how to adjust the network’s weights to improve these predictions. This process enables neural networks to learn from their mistakes.
To understand backward propagation, let’s continue with our MNIST example. When the network predicts a “3” for an image of “7”, we need a systematic way to adjust weights throughout the network to make this mistake less likely in the future. Backward propagation provides this by calculating how each weight contributed to the error.
The process begins at the network’s output, where we compare the predicted digit probabilities with the true label. This error then flows backward through the network, with each layer’s weights receiving an update signal based on their contribution to the final prediction. The computation follows the chain rule of calculus19, breaking down the complex relationship between weights and final error into manageable steps.
19 Chain rule of calculus: A basic theorem in calculus stating that the derivative of a composite function is the product of the derivative of the outer function and the derivative of the inner function.
Cost functions play a crucial role in helping neural networks learn by providing a measurable way to evaluate how well the network is performing and guide the optimization process.
Gradient descent – Part 1 - 3Blue1Brown
Gradient descent – Part 2 - 3Blue1Brown
Gradient Flow
The flow of gradients through a neural network follows a path opposite to the forward propagation. Starting from the loss at the output layer, gradients propagate backwards, computing how each layer, and ultimately each weight, influenced the final prediction error.
In our MNIST example, consider what happens when the network misclassifies a “7” as a “3”. The loss function generates an initial error signal at the output layer, essentially indicating that the probability for “7” should increase while the probability for “3” should decrease. This error signal then propagates backward through the network layers.
For a network with L layers, the gradient flow can be expressed mathematically. At each layer l, we compute how the layer’s output affected the final loss: \[ \frac{\partial L}{\partial \mathbf{A}^{(l)}} = \frac{\partial L}{\partial \mathbf{A}^{(l+1)}} \frac{\partial \mathbf{A}^{(l+1)}}{\partial \mathbf{A}^{(l)}} \]
This computation cascades backward through the network, with each layer’s gradients depending on the gradients computed in the layer previous to it. The process reveals how each layer’s transformation contributed to the final prediction error. For instance, if certain weights in an early layer strongly influenced a misclassification, they will receive larger gradient values, indicating a need for more substantial adjustment.
However, this process faces important challenges in deep networks. As gradients flow backward through many layers, they can either vanish or explode. When gradients are repeatedly multiplied through many layers, they can become exponentially small, particularly with sigmoid or tanh activation functions. This causes early layers to learn very slowly or not at all, as they receive negligible (vanishing) updates. Conversely, if gradient values are consistently greater than 1, they can grow exponentially, leading to unstable training and destructive weight updates.
Gradient Computation
The actual computation of gradients involves calculating several partial derivatives at each layer. For each layer, we need to determine how changes in weights, biases, and activations affect the final loss. These computations follow directly from the chain rule of calculus but must be implemented efficiently for practical neural network training.
At each layer \(l\), we compute three main gradient components:
Weight Gradients: \[ \frac{\partial L}{\partial \mathbf{W}^{(l)}} = \frac{\partial L}{\partial \mathbf{Z}^{(l)}} {\mathbf{A}^{(l-1)}}^T \]
Bias Gradients: \[ \frac{\partial L}{\partial \mathbf{b}^{(l)}} = \frac{\partial L}{\partial \mathbf{Z}^{(l)}} \]
Input Gradients (for propagating to previous layer): \[ \frac{\partial L}{\partial \mathbf{A}^{(l-1)}} = {\mathbf{W}^{(l)}}^T \frac{\partial L}{\partial \mathbf{Z}^{(l)}} \]
In our MNIST example, consider the final layer where the network outputs digit probabilities. If the network predicted \([0.1, 0.2, 0.5,\ldots, 0.05]\) for an image of “7”, the gradient computation would:
- Start with the error in these probabilities
- Compute how weight adjustments would affect this error
- Propagate these gradients backward to help adjust earlier layer weights
Implementation Aspects
The practical implementation of backward propagation requires careful consideration of computational resources and memory management. These implementation details significantly impact training efficiency and scalability.
Memory requirements during backward propagation stem from two main sources. First, we need to store the intermediate activations from the forward pass, as these are required for computing gradients. For our MNIST network with a batch size of 32, each layer’s activations must be maintained:
- Input layer: \(32\times 784\) values
- Hidden layers: \(32\times h\) values (where \(h\) is the layer width)
- Output layer: \(32\times 10\) values
Second, we need storage for the gradients themselves. For each layer, we must maintain gradients of similar dimensions to the weights and biases. Taking our previous example of a network with hidden layers of size 128, 256, and 128, this means storing:
- First layer gradients: \(784\times 128\) values
- Second layer gradients: \(128\times 256\) values
- Third layer gradients: \(256\times 128\) values
- Output layer gradients: \(128\times 10\) values
The computational pattern of backward propagation follows a specific sequence:
- Compute gradients at current layer
- Update stored gradients
- Propagate error signal to previous layer
- Repeat until input layer is reached
For batch processing, these computations are performed simultaneously across all examples in the batch, enabling efficient use of matrix operations and parallel processing capabilities.
Optimization Process
Gradient Descent Basics
The optimization process adjusts the network’s weights to improve its predictions. Using a method called gradient descent, the network calculates how much each weight contributes to the error and updates it to reduce the loss. This process is repeated over many iterations, gradually refining the network’s ability to make accurate predictions.
The fundamental update rule for gradient descent is: \[ \theta_{\text{new}} = \theta_{\text{old}} - \alpha \nabla_{\theta}L \] where \(\theta\) represents any network parameter (weights or biases), \(\alpha\) is the learning rate, and \(\nabla_{\theta}L\) is the gradient of the loss with respect to that parameter.
For our MNIST example, this means adjusting weights to improve digit classification accuracy. If the network frequently confuses “7”s with “1”s, gradient descent will modify the weights to better distinguish between these digits. The learning rate \(\alpha\) controls how large these adjustments are—too large, and the network might overshoot optimal values; too small, and training will progress very slowly.
The mathematical foundation of backpropagation involves computing partial derivatives through the chain rule, allowing each weight to understand its specific contribution to the overall error.
Backpropagation - 3Blue1Brown
Batch Processing
Neural networks typically process multiple examples simultaneously during training, an approach known as mini-batch gradient descent. Rather than updating weights after each individual image, we compute the average gradient over a batch of examples before performing the update.
For a batch of size \(B\), the loss gradient becomes: \[ \nabla_{\theta}L_{\text{batch}} = \frac{1}{B}\sum_{i=1}^B \nabla_{\theta}L_i \]
In our MNIST training, with a typical batch size of 32, this means:
- Process 32 images through forward propagation
- Compute loss for all 32 predictions
- Average the gradients across all 32 examples
- Update weights using this averaged gradient
Training Loop
The complete training process combines forward propagation, backward propagation, and weight updates into a systematic training loop. This loop repeats until the network achieves satisfactory performance or reaches a predetermined number of iterations.
A single pass through the entire training dataset is called an epoch. For MNIST, with 60,000 training images and a batch size of 32, each epoch consists of 1,875 batch iterations. The training loop structure is:
- For each epoch:
- Shuffle training data to prevent learning order-dependent patterns
- For each batch:
- Perform forward propagation
- Compute loss
- Execute backward propagation
- Update weights using gradient descent
- Evaluate network performance
During training, we monitor several key metrics:
- Training loss: average loss over recent batches
- Validation accuracy: performance on held-out test data
- Learning progress: how quickly the network improves
For our digit recognition task, we might observe the network’s accuracy improve from 10% (random guessing) to over 95% through multiple epochs of training.
Practical Considerations
The successful implementation of neural network training requires attention to several key practical aspects that significantly impact learning effectiveness. These considerations bridge the gap between theoretical understanding and practical implementation.
Learning rate selection is perhaps the most critical parameter affecting training. For our MNIST network, the choice of learning rate dramatically influences the training dynamics. A large learning rate of 0.1 might cause unstable training where the loss oscillates or explodes as weight updates overshoot optimal values. Conversely, a very small learning rate of 0.0001 might result in extremely slow convergence, requiring many more epochs to achieve good performance. A moderate learning rate of 0.01 often provides a good balance between training speed and stability, allowing the network to make steady progress while maintaining stable learning.
Convergence monitoring provides crucial feedback during the training process. As training progresses, we typically observe the loss value stabilizing around a particular value, indicating the network is approaching a local optimum. The validation accuracy often plateaus as well, suggesting the network has extracted most of the learnable patterns from the data. The gap between training and validation performance offers insights into whether the network is overfitting or generalizing well to new examples.
Resource requirements become increasingly important as we scale neural network training. The memory footprint must accommodate both model parameters and the intermediate computations needed for backpropagation. Computation scales linearly with batch size, affecting training speed and hardware utilization. Modern training often leverages GPU acceleration, making efficient use of parallel computing capabilities crucial for practical implementation.
Training neural networks also presents several fundamental challenges. Overfitting occurs when the network becomes too specialized to the training data, performing well on seen examples but poorly on new ones. Gradient instability can manifest as either vanishing or exploding gradients, making learning difficult. The interplay between batch size, available memory, and computational resources often requires careful balancing to achieve efficient training while working within hardware constraints.
Prediction Phase
Neural networks serve two distinct purposes: learning from data during training and making predictions during inference. While we’ve explored how networks learn through forward propagation, backward propagation, and weight updates, the prediction phase operates differently. During inference, networks use their learned parameters to transform inputs into outputs without the need for learning mechanisms. This simpler computational process still requires careful consideration of how data flows through the network and how system resources are utilized. Understanding the prediction phase is crucial as it represents how neural networks are actually deployed to solve real-world problems, from classifying images to generating text predictions.
Inference Basics
Training vs Inference
The computation flow fundamentally changes when moving from training to inference. While training requires both forward and backward passes through the network to compute gradients and update weights, inference involves only the forward pass computation. This simpler flow means that each layer needs to perform only one set of operations, transforming inputs to outputs using the learned weights, rather than tracking intermediate values for gradient computation, as illustrated in Figure 16.
Parameter freezing is another another major distinction between training and inference phases. During training, weights and biases continuously update to minimize the loss function. In inference, these parameters remain fixed, acting as static transformations learned from the training data. This freezing of parameters not only simplifies computation but also enables optimizations impossible during training, such as weight quantization or pruning.
The structural difference between training loops and inference passes significantly impacts system design. Training operates in an iterative loop, processing multiple batches of data repeatedly across many epochs to refine the network’s parameters. Inference, in contrast, typically processes each input just once, generating predictions in a single forward pass. This fundamental shift from iterative refinement to single-pass prediction influences how we architect systems for deployment.
Memory and computation requirements differ substantially between training and inference. Training demands considerable memory to store intermediate activations for backpropagation, gradients for weight updates, and optimization states. Inference eliminates these memory-intensive requirements, needing only enough memory to store the model parameters and compute a single forward pass. This reduction in memory footprint, coupled with simpler computation patterns, enables inference to run efficiently on a broader range of devices, from powerful servers to resource-constrained edge devices.
In general, the training phase requires more computational resources and memory for learning, while inference is streamlined for efficient prediction. Table 5 summarizes the key differences between training and inference.
| Aspect | Training | Inference |
|---|---|---|
| Computation Flow | Forward and backward passes, gradient computation | Forward pass only, direct input to output |
| Parameters | Continuously updated weights and biases | Fixed/frozen weights and biases |
| Processing Pattern | Iterative loops over multiple epochs | Single pass through the network |
| Memory Requirements | High – stores activations, gradients, optimizer state | Lower– stores only model | parameters and current input |
| Computational Needs | Heavy – gradient updates, backpropagation | Lighter – matrix multiplication only |
| Hardware Requirements | GPUs/specialized hardware for efficient training | Can run on simpler devices, including mobile/edge |
This stark contrast between training and inference phases highlights why system architectures often differ significantly between development and deployment environments. While training requires substantial computational resources and specialized hardware, inference can be optimized for efficiency and deployed across a broader range of devices.
Basic Pipeline
The implementation of neural networks in practical applications requires a complete processing pipeline that extends beyond the network itself. This pipeline, which is illustrated in Figure 17 transforms raw inputs into meaningful outputs through a series of distinct stages, each essential for the system’s operation. Understanding this complete pipeline provides critical insights into the design and deployment of machine learning systems.
The key thing to notice from the figure is that machine learning systems operate as hybrid architectures that combine conventional computing operations with neural network computations. The neural network component, focused on learned transformations through matrix operations, represents just one element within a broader computational framework. This framework encompasses both the preparation of input data and the interpretation of network outputs, processes that rely primarily on traditional computing methods.
Consider how data flows through the pipeline in Figure 17:
- Raw inputs arrive in their original form, which might be images, text, sensor readings, or other data types
- Pre-processing transforms these inputs into a format suitable for neural network consumption
- The neural network performs its learned transformations
- Raw outputs emerge from the network, often in numerical form
- Post-processing converts these outputs into meaningful, actionable results
This pipeline structure reveals several fundamental characteristics of machine learning systems. The neural network, despite its computational sophistication, functions as a component within a larger system. Performance bottlenecks may arise at any stage of the pipeline, not exclusively within the neural network computation. System optimization must therefore consider the entire pipeline rather than focusing solely on the neural network’s operation.
The hybrid nature of this architecture has significant implications for system implementation. While neural network computations may benefit from specialized hardware accelerators, pre- and post-processing operations typically execute on conventional processors. This distribution of computation across heterogeneous hardware resources represents a fundamental consideration in system design.
Pre-processing
The pre-processing stage transforms raw inputs into a format suitable for neural network computation. While often overlooked in theoretical discussions, this stage forms a critical bridge between real-world data and neural network operations. Consider our MNIST digit recognition example: before a handwritten digit image can be processed by the neural network we designed earlier, it must undergo several transformations. Raw images of handwritten digits arrive in various formats, sizes, and pixel value ranges. For instance, in Figure 18, we see that the digits are all of different sizes, and even the number 6 is written differently by the same person.
The pre-processing stage standardizes these inputs through conventional computing operations:
- Image scaling to the required \(28\times 28\) pixel dimensions, camera images are usually large(r).
- Pixel value normalization from \([0,255]\) to \([0,1]\), most cameras generate colored images.
- Flattening the 2D image array into a 784-dimensional vector, preparing it for the neural network.
- Basic validation to ensure data integrity, making sure the network predicted correctly.
What distinguishes pre-processing from neural network computation is its reliance on traditional computing operations rather than learned transformations. While the neural network learns to recognize digits through training, pre-processing operations remain fixed, deterministic transformations. This distinction has important system implications: pre-processing operates on conventional CPUs rather than specialized neural network hardware, and its performance characteristics follow traditional computing patterns.
The effectiveness of pre-processing directly impacts system performance. Poor normalization can lead to reduced accuracy, inconsistent scaling can introduce artifacts, and inefficient implementation can create bottlenecks. Understanding these implications helps in designing robust machine learning systems that perform well in real-world conditions.
Inference
The inference phase represents the operational state of a neural network, where learned parameters are used to transform inputs into predictions. Unlike the training phase we discussed earlier, inference focuses solely on forward computation with fixed parameters.
Network Initialization
Before processing any inputs, the neural network must be properly initialized for inference. This initialization phase involves loading the model parameters learned during training into memory. For our MNIST digit recognition network, this means loading specific weight matrices and bias vectors for each layer. Let’s examine the exact memory requirements for our architecture:
- Input to first hidden layer:
- Weight matrix: \(784\times 100 = 78,400\) parameters
- Bias vector: 100 parameters
- First to second hidden layer:
- Weight matrix: \(100\times 100 = 10,000\) parameters
- Bias vector: 100 parameters
- Second hidden layer to output:
- Weight matrix: \(100\times 10 = 1,000\) parameters
- Bias vector: 10 parameters
In total, the network requires storage for 89,610 learned parameters (89,400 weights plus 210 biases). Beyond these fixed parameters, memory must also be allocated for intermediate activations during forward computation. For processing a single image, this means allocating space for:
- First hidden layer activations: 100 values
- Second hidden layer activations: 100 values
- Output layer activations: 10 values
This memory allocation pattern differs significantly from training, where additional memory was needed for gradients, optimizer states, and backpropagation computations.
Forward Pass Computation
During inference, data propagates through the network’s layers using the initialized parameters. This forward propagation process, while similar in structure to its training counterpart, operates with different computational constraints and optimizations. The computation follows a deterministic path from input to output, transforming the data at each layer using learned parameters.
For our MNIST digit recognition network, consider the precise computations at each layer. The network processes a pre-processed image represented as a 784-dimensional vector through successive transformations:
- First Hidden Layer Computation:
- Input transformation: 784 inputs combine with 78,400 weights through matrix multiplication
- Linear computation: \(\mathbf{z}^{(1)} = \mathbf{x}\mathbf{W}^{(1)} + \mathbf{b}^{(1)}\)
- Activation: \(\mathbf{a}^{(1)} = \text{ReLU}(\mathbf{z}^{(1)})\)
- Output: 100-dimensional activation vector
- Second Hidden Layer Computation:
- Input transformation: 100 values combine with 10,000 weights
- Linear computation: \(\mathbf{z}^{(2)} = \mathbf{a}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}\)
- Activation: \(\mathbf{a}^{(2)} = \text{ReLU}(\mathbf{z}^{(2)})\)
- Output: 100-dimensional activation vector
- Output Layer Computation:
- Final transformation: 100 values combine with 1,000 weights
- Linear computation: \(\mathbf{z}^{(3)} = \mathbf{a}^{(2)}\mathbf{W}^{(3)} + \mathbf{b}^{(3)}\)
- Activation: \(\mathbf{a}^{(3)} = \text{softmax}(\mathbf{z}^{(3)})\)
- Output: 10 probability values
Table 6 shows how these computations, while mathematically identical to training-time forward propagation, show important operational differences:
| Characteristic | Training Forward Pass | Inference Forward Pass |
|---|---|---|
| Activation Storage | Maintains complete activation history for backpropagation | Retains only current layer activations |
| Memory Pattern | Preserves intermediate states throughout forward pass | Releases memory after layer computation completes |
| Computational Flow | Structured for gradient computation preparation | Optimized for direct output generation |
| Resource Profile | Higher memory requirements for training operations | Minimized memory footprint for efficient execution |
This streamlined computation pattern enables efficient inference while maintaining the network’s learned capabilities. The reduction in memory requirements and simplified computational flow make inference particularly suitable for deployment in resource-constrained environments, such as Mobile ML and Tiny ML.
Resource Requirements
Neural networks consume computational resources differently during inference compared to training. During inference, resource utilization focuses primarily on efficient forward pass computation and minimal memory overhead. Let’s examine the specific requirements for our MNIST digit recognition network.
Memory requirements during inference can be precisely quantified:
- Static Memory (Model Parameters):
- Layer 1: 78,400 weights + 100 biases
- Layer 2: 10,000 weights + 100 biases
- Layer 3: 1,000 weights + 10 biases
- Total: 89,610 parameters (\(\approx 358.44\) KB at 32-bit floating point precision)
- Dynamic Memory (Activations):
- Layer 1 output: 100 values
- Layer 2 output: 100 values
- Layer 3 output: 10 values
- Total: 210 values (\(\approx 0.84\) KB at 32-bit floating point precision)
Computational requirements follow a fixed pattern for each input:
- First layer: 78,400 multiply-adds
- Second layer: 10,000 multiply-adds
- Output layer: 1,000 multiply-adds
- Total: 89,400 multiply-add operations per inference
This resource profile stands in stark contrast to training requirements, where additional memory for gradients and computational overhead for backpropagation significantly increase resource demands. The predictable, streamlined nature of inference computations enables various optimization opportunities and efficient hardware utilization.
Optimization Opportunities
The fixed nature of inference computation presents several opportunities for optimization that are not available during training. Once a neural network’s parameters are frozen, the predictable pattern of computation allows for systematic improvements in both memory usage and computational efficiency.
Batch size selection represents a fundamental trade-off in inference optimization. During training, large batches were necessary for stable gradient computation, but inference offers more flexibility. Processing single inputs minimizes latency, making it ideal for real-time applications where immediate responses are crucial. However, batch processing can significantly improve throughput by better utilizing parallel computing capabilities, particularly on GPUs. For our MNIST network, consider the memory implications: processing a single image requires storing 210 activation values, while a batch of 32 images requires 6,720 activation values but can process images up to 32 times faster on parallel hardware.
Memory management during inference can be significantly more efficient than during training. Since intermediate values are only needed for forward computation, memory buffers can be carefully managed and reused. The activation values from each layer need only exist until the next layer’s computation is complete. This enables in-place operations where possible, reducing the total memory footprint. Furthermore, the fixed nature of inference allows for precise memory alignment and access patterns optimized for the underlying hardware architecture.
Hardware-specific optimizations become particularly important during inference. On CPUs, computations can be organized to maximize cache utilization and take advantage of SIMD (Single Instruction, Multiple Data) capabilities. GPU deployments benefit from optimized matrix multiplication routines and efficient memory transfer patterns. These optimizations extend beyond pure computational efficiency, as they can significantly impact power consumption and hardware utilization, critical factors in real-world deployments.
The predictable nature of inference also enables more aggressive optimizations like reduced numerical precision. While training typically requires 32-bit floating-point precision to maintain stable gradient computation, inference can often operate with 16-bit or even 8-bit precision while maintaining acceptable accuracy. For our MNIST network, this could reduce the memory footprint from 358.44 KB to 179.22 KB or even 89.61 KB, with corresponding improvements in computational efficiency.
These optimization principles, while illustrated through our simple MNIST feedforward network, represent only the foundation of neural network optimization. More sophisticated architectures introduce additional considerations and opportunities. Convolutional Neural Networks (CNNs), for instance, present unique optimization opportunities in handling spatial data and filter operations. Recurrent Neural Networks (RNNs) require careful consideration of sequential computation and state management. Transformer architectures introduce distinct patterns of attention computation and memory access. These architectural variations and their optimizations will be explored in detail in subsequent chapters, particularly when we discuss deep learning architectures, model optimizations, and efficient AI implementations.
Post-processing
The transformation of neural network outputs into actionable predictions requires a return to traditional computing paradigms. Just as pre-processing bridges real-world data to neural computation, post-processing bridges neural outputs back to conventional computing systems. This completes the hybrid computing pipeline we examined earlier, where neural and traditional computing operations work in concert to solve real-world problems.
The complexity of post-processing extends beyond simple mathematical transformations. Real-world systems must handle uncertainty, validate outputs, and integrate with larger computing systems. In our MNIST example, a digit recognition system might require not just the most likely digit, but also confidence measures to determine when human intervention is needed. This introduces additional computational steps: confidence thresholds, secondary prediction checks, and error handling logic, all of which are implemented in traditional computing frameworks.
The computational requirements of post-processing differ significantly from neural network inference. While inference benefits from parallel processing and specialized hardware, post-processing typically runs on conventional CPUs and follows sequential logic patterns. This return to traditional computing brings both advantages and constraints. Operations are more flexible and easier to modify than neural computations, but they may become bottlenecks if not carefully implemented. For instance, computing softmax probabilities20 for a batch of predictions requires different optimization strategies than the matrix multiplications of neural network layers.
20 Softmax: A function used in machine learning to convert a vector of values into a probability distribution.
System integration considerations often dominate post-processing design. Output formats must match downstream system requirements, error handling must align with broader system protocols, and performance must meet system-level constraints. In a complete mail sorting system, the post-processing stage must not only identify digits but also format these predictions for the sorting machinery, handle uncertainty cases appropriately, and maintain processing speeds that match physical mail flow rates.
This return to traditional computing paradigms completes the hybrid nature of machine learning systems. Just as pre-processing prepared real-world data for neural computation, post-processing adapts neural outputs for real-world use. Understanding this hybrid nature, the interplay between neural and traditional computing, is essential for designing and implementing effective machine learning systems.
Case Study: USPS Postal Service
Real-world Problem
The United States Postal Service (USPS) processes over 100 million pieces of mail daily, each requiring accurate routing based on handwritten ZIP codes. In the early 1990s, this task was primarily performed by human operators, making it one of the largest manual data entry operations in the world. The automation of this process through neural networks represents one of the earliest and most successful large-scale deployments of artificial intelligence, embodying many of the principles we’ve explored in this chapter.
Consider the complexity of this task: a ZIP code recognition system must process images of handwritten digits captured under varying conditions, different writing styles, pen types, paper colors, and environmental factors (see Figure 19). It must make accurate predictions within milliseconds to maintain mail processing speeds. Furthermore, errors in recognition can lead to significant delays and costs from misrouted mail. This real-world constraint meant the system needed not just high accuracy, but also reliable measures of prediction confidence to identify when human intervention was necessary.
This challenging environment presented requirements spanning every aspect of neural network implementation we’ve discussed, from biological inspiration to practical deployment considerations. The success or failure of the system would depend not just on the neural network’s accuracy, but on the entire pipeline from image capture through to final sorting decisions.
System Development
The development of the USPS digit recognition system required careful consideration at every stage, from data collection to deployment. This process illustrates how theoretical principles of neural networks translate into practical engineering decisions.
Data collection presented the first major challenge. Unlike controlled laboratory environments, postal facilities needed to process mail pieces with tremendous variety. The training dataset had to capture this diversity. Digits written by people of different ages, educational backgrounds, and writing styles formed just part of the challenge. Envelopes came in varying colors and textures, and images were captured under different lighting conditions and orientations. This extensive data collection effort later contributed to the creation of the MNIST database we’ve used in our examples.
The network architecture design required balancing multiple constraints. While deeper networks might achieve higher accuracy, they would also increase processing time and computational requirements. Processing \(28\times 28\) pixel images of individual digits needed to complete within strict time constraints while running reliably on available hardware. The network had to maintain consistent accuracy across varying conditions, from well-written digits to hurried scrawls.
Training the network introduced additional complexity. The system needed to achieve high accuracy not just on a test dataset, but on the endless variety of real-world handwriting styles. Careful preprocessing normalized input images to account for variations in size and orientation. Data augmentation techniques increased the variety of training samples. The team validated performance across different demographic groups and tested under actual operating conditions to ensure robust performance.
The engineering team faced a critical decision regarding confidence thresholds21. Setting these thresholds too high would route too many pieces to human operators, defeating the purpose of automation. Setting them too low would risk delivery errors. The solution emerged from analyzing the confidence distributions of correct versus incorrect predictions. This analysis established thresholds that optimized the tradeoff between automation rate and error rate, ensuring efficient operation while maintaining acceptable accuracy.
21 Confidence thresholds: Predetermined limits set to decide when the model’s prediction is to be accepted. Influences system efficiency and accuracy.
Complete Pipeline
Following a single piece of mail through the USPS recognition system illustrates how the concepts we’ve discussed integrate into a complete solution. The journey from physical mail piece to sorted letter demonstrates the interplay between traditional computing, neural network inference, and physical machinery.
The process begins when an envelope reaches the imaging station. High-speed cameras capture the ZIP code region at rates exceeding several pieces of mail (e.g. 10) pieces per second. This image acquisition process must adapt to varying envelope colors, handwriting styles, and environmental conditions. The system must maintain consistent image quality despite the speed of operation, as motion blur and proper illumination present significant engineering challenges.
Pre-processing transforms these raw camera images into a format suitable for neural network analysis. The system must locate the ZIP code region, segment individual digits, and normalize each digit image. This stage employs traditional computer vision techniques: image thresholding22 adapts to envelope background color, connected component analysis23 identifies individual digits, and size normalization produces standard \(28\times 28\) pixel images. Speed remains critical; these operations must complete within milliseconds to maintain throughput.
22 Image Thresholding: A technique in image processing that converts grayscale images into binary images.
23 Connected Component Analysis: An operation in image processing used to distinguish and identify disjoint objects within an image.
The neural network then processes each normalized digit image. The trained network, with its 89,610 parameters (as we detailed earlier), performs forward propagation to generate predictions. Each digit passes through two hidden layers of 100 neurons each, ultimately producing ten output values representing digit probabilities. This inference process, while computationally intensive, benefits from the optimizations we discussed in the previous section.
Post-processing converts these neural network outputs into sorting decisions. The system applies confidence thresholds to each digit prediction. A complete ZIP code requires high confidence in all five digits, a single uncertain digit flags the entire piece for human review. When confidence meets thresholds, the system transmits sorting instructions to mechanical systems that physically direct the mail piece to its appropriate bin.
The entire pipeline operates under strict timing constraints. From image capture to sorting decision, processing must complete before the mail piece reaches its sorting point. The system maintains multiple pieces in various pipeline stages simultaneously, requiring careful synchronization between computing and mechanical systems. This real-time operation illustrates why the optimizations we discussed in inference and post-processing become crucial in practical applications.
Results and Impact
The implementation of neural network-based ZIP code recognition transformed USPS mail processing operations. By 2000, several facilities across the country utilized this technology, processing millions of mail pieces daily. This real-world deployment demonstrated both the potential and limitations of neural network systems in mission-critical applications.
Performance metrics revealed interesting patterns that validate many of the principles discussed earlier in this chapter. The system achieved its highest accuracy on clearly written digits, similar to those in the training data. However, performance varied significantly with real-world factors. Lighting conditions affected pre-processing effectiveness. Unusual writing styles occasionally confused the neural network. Environmental vibrations could also impact image quality. These challenges led to continuous refinements in both the physical system and the neural network pipeline.
The economic impact proved substantial. Prior to automation, manual sorting required operators to read and key in ZIP codes at an average rate of one piece per second. The neural network system processed pieces at ten times this rate while reducing labor costs and error rates. However, the system didn’t eliminate human operators entirely; their role shifted to handling uncertain cases and maintaining system performance. This hybrid approach, combining artificial and human intelligence, became a model for other automation projects.
The system also revealed important lessons about deploying neural networks in production environments. Training data quality proved crucial; the network performed best on digit styles well-represented in its training set. Regular retraining helped adapt to evolving handwriting styles. Maintenance required both hardware specialists and machine learning experts, introducing new operational considerations. These insights influenced subsequent deployments of neural networks in other industrial applications.
Perhaps most importantly, this implementation demonstrated how theoretical principles translate into practical constraints. The biological inspiration of neural networks provided the foundation for digit recognition, but successful deployment required careful consideration of system-level factors: processing speed, error handling, maintenance requirements, and integration with existing infrastructure. These lessons continue to inform modern machine learning deployments, where similar challenges of scale, reliability, and integration persist.
Key Takeaways
The USPS ZIP code recognition system is an excellent example of the journey from biological inspiration to practical neural network deployment that we’ve explored throughout this chapter. It demonstrates how the basic principles of neural computation, from pre-processing through inference to post-processing, come together in solving real-world problems.
The system’s development shows why understanding both the theoretical foundations and practical considerations is crucial. While the biological visual system processes handwritten digits effortlessly, translating this capability into an artificial system required careful consideration of network architecture, training procedures, and system integration.
The success of this early large-scale neural network deployment helped establish many practices we now consider standard: the importance of comprehensive training data, the need for confidence metrics, the role of pre- and post-processing, and the critical nature of system-level optimization.
As we move forward to explore more complex architectures and applications in subsequent chapters, this case study reminds us that successful deployment requires mastery of both fundamental principles and practical engineering considerations.
Summary
In this chapter, we explored the foundational concepts of neural networks, bridging the gap between biological inspiration and artificial implementation. We began by examining the remarkable efficiency and adaptability of the human brain, uncovering how its principles influence the design of artificial neurons. From there, we delved into the behavior of a single artificial neuron, breaking down its components and operations. This understanding laid the groundwork for constructing neural networks, where layers of interconnected neurons collaborate to tackle increasingly complex tasks.
The progression from single neurons to network-wide behavior underscored the power of hierarchical learning, where each layer extracts and transforms patterns from raw data into meaningful abstractions. We examined both the learning process and the prediction phase, showing how neural networks first refine their performance through training and then deploy that knowledge through inference. The distinction between these phases revealed important system-level considerations for practical implementations.
Our exploration of the complete processing pipeline, from pre-processing through inference to post-processing, highlighted the hybrid nature of machine learning systems, where traditional computing and neural computation work together. The USPS case study demonstrated how these theoretical principles translate into practical applications, revealing both the power and complexity of deployed neural networks. These real-world considerations, from data collection to system integration, form an essential part of understanding machine learning systems.
In the next chapter, we will expand on these ideas, exploring sophisticated deep learning architectures such as convolutional and recurrent neural networks. These architectures are tailored to process diverse data types, from images and text to time series, enabling breakthroughs across a wide range of applications. By building on the concepts introduced here, we will gain a deeper appreciation for the design, capabilities, and versatility of modern deep learning systems.